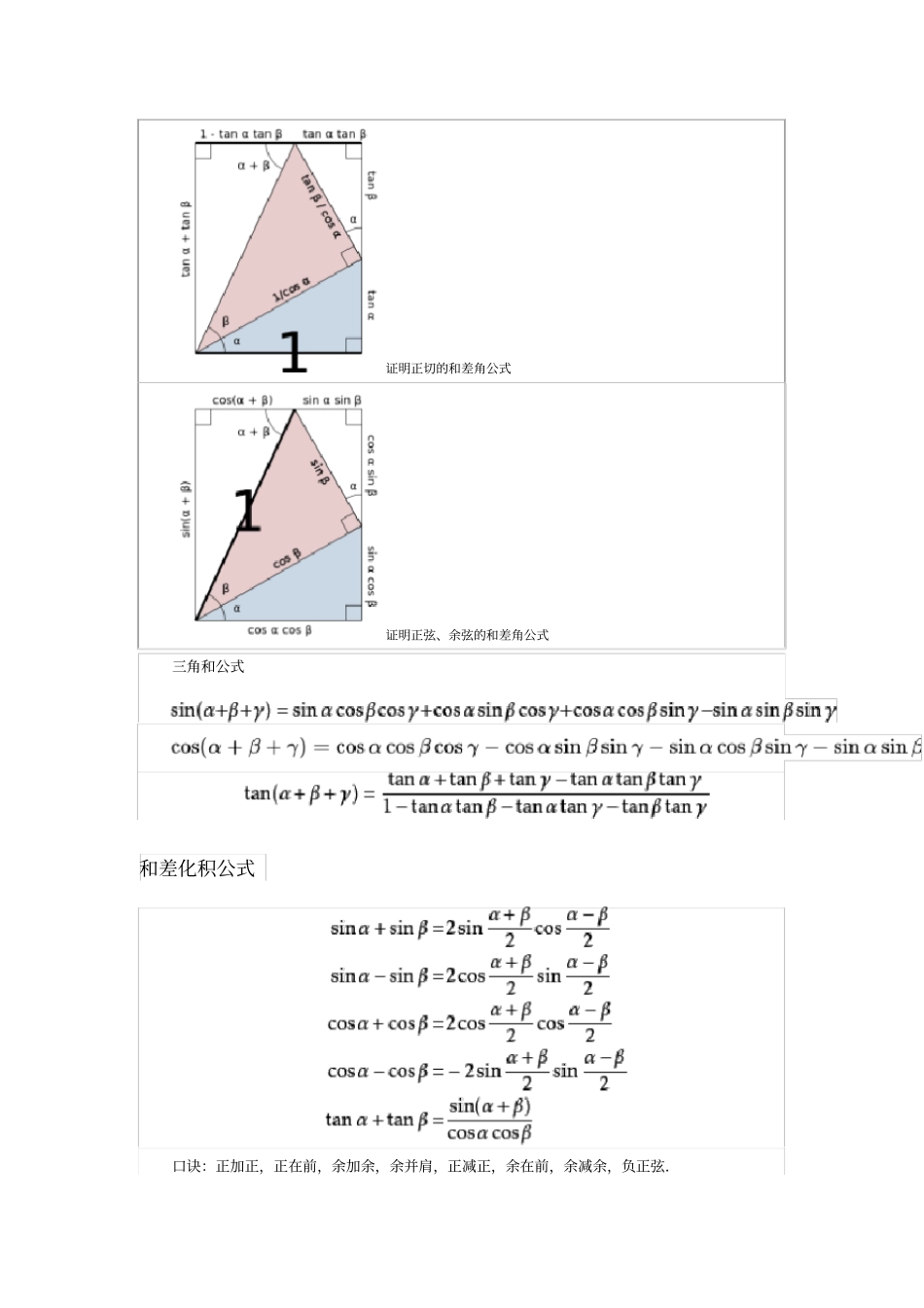
数学函数公式一、记忆技巧1、《集合与函数》内容子交并补集,还有幂指对函数。性质奇偶与增减,观察图象最明显。复合函数式出现,性质乘法法则辨,若要详细证明它,还须将那定义抓。指数与对数函数,两者互为反函数。底数非1的正数,1两边增减变故。函数定义域好求。分母不能等于0,偶次方根须非负,零和负数无对数;正切函数角不直,余切函数角不平;其余函数实数集,多种情况求交集。两个互为反函数,单调性质都相同;图象互为轴对称,Y=X是对称轴;求解非常有规律,反解换元定义域;反函数的定义域,原来函数的值域。幂函数性质易记,指数化既约分数;函数性质看指数,奇母奇子奇函数,奇母偶子偶函数,偶母非奇偶函数;图象第一象限内,函数增减看正负。2、《三角函数》三角函数是函数,象限符号坐标注。函数图象单位圆,周期奇偶增减现。同角关系很重要,化简证明都需要。正六边形顶点处,从上到下弦切割;中心记上数字1,连结顶点三角形;向下三角平方和,倒数关系是对角,顶点任意一函数,等于后面两根除。诱导公式就是好,负化正后大化小,变成税角好查表,化简证明少不了。二的一半整数倍,奇数化余偶不变,将其后者视锐角,符号原来函数判。两角和的余弦值,化为单角好求值,余弦积减正弦积,换角变形众公式。和差化积须同名,互余角度变名称。计算证明角先行,注意结构函数名,保持基本量不变,繁难向着简易变。逆反原则作指导,升幂降次和差积。条件等式的证明,方程思想指路明。万能公式不一般,化为有理式居先。公式顺用和逆用,变形运用加巧用;1加余弦想余弦,1减余弦想正弦,幂升一次角减半,升幂降次它为范;三角函数反函数,实质就是求角度,先求三角函数值,再判角取值范围;利用直角三角形,形象直观好换名,简单三角的方程,化为最简求解集。二、基本公式和差角公式二角和差公式证明如图:负号的情况只需要用-β代替β即可.cot(α+β)推导只需把角α对边设为1,过程与tan(α+β)相同.证明正切的和差角公式证明正弦、余弦的和差角公式三角和公式和差化积公式口诀:正加正,正在前,余加余,余并肩,正减正,余在前,余减余,负正弦.积化和差公式倍角公式二倍角公式三倍角公式证明:sin3a=sin(a+2a)=sin2a·cosa+cos2a·sina=2sina(1-sin2a)+(1-2sin2a)sina=3sina-4sin3acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos2a-1)cosa-2(1-cos2a)cosa=4cos3a-3cosasin3acos3a上述两式相比可得:tan3a四倍角公式sin4a=-4×[cosa·sina·(2×sin2a-1)]cos4a=8cos4a-8cos2a+1tan4a=(4tana-4tan3a)/(1-6tan2a+tan4a)[3]五倍角公式n倍角公式应用欧拉公式:.上式用于求n倍角的三角函数时,可变形为:所以其中,Re表示取实数部分,Im表示取虚数部分.而所以半角公式(正负由所在的象限决定)万能公式辅助角公式证明:由于,显然,且故有:其它公式编辑正弦定理余弦定理详见词条:正弦定理在任意△ABC中,角A、B、C所对的边长分别为a、b、c,三角形外接圆的半径为R.则有[4]:正弦定理变形可得:余弦定理详见词条:余弦定理余弦定理对于如图所示的边长为a、b、c而相应角为α、β、γ的△ABC,有:也可表示为:降幂公式sin2α=[1-cos(2α)]/2cos2α=[1+cos(2α)]/2tan2α=[1-cos(2α)]/[1+cos(2α)]幂级数c0+c1x+c2x2+...+cnxn+...=∑cnxn(n=0..∞)c0+c1(x-a)+c2(x-a)2+...+cn(x-a)n+...=∑cn(x-a)n(n=0..∞)它们的各项都是正整数幂的幂函数,其中c0,c1,c2,...cn...及a都是常数,这种级数称为幂级数。泰勒展开式泰勒展开式又叫幂级数展开法实用幂级数:,(!!表示双阶乘)在解初等三角函数时,只需记住公式便可轻松作答,在竞赛中,往往会用到与图像结合的方法求三角函数值、三角函数不等式、面积等等。万能公式傅里叶级数傅里叶级数又称三角级数