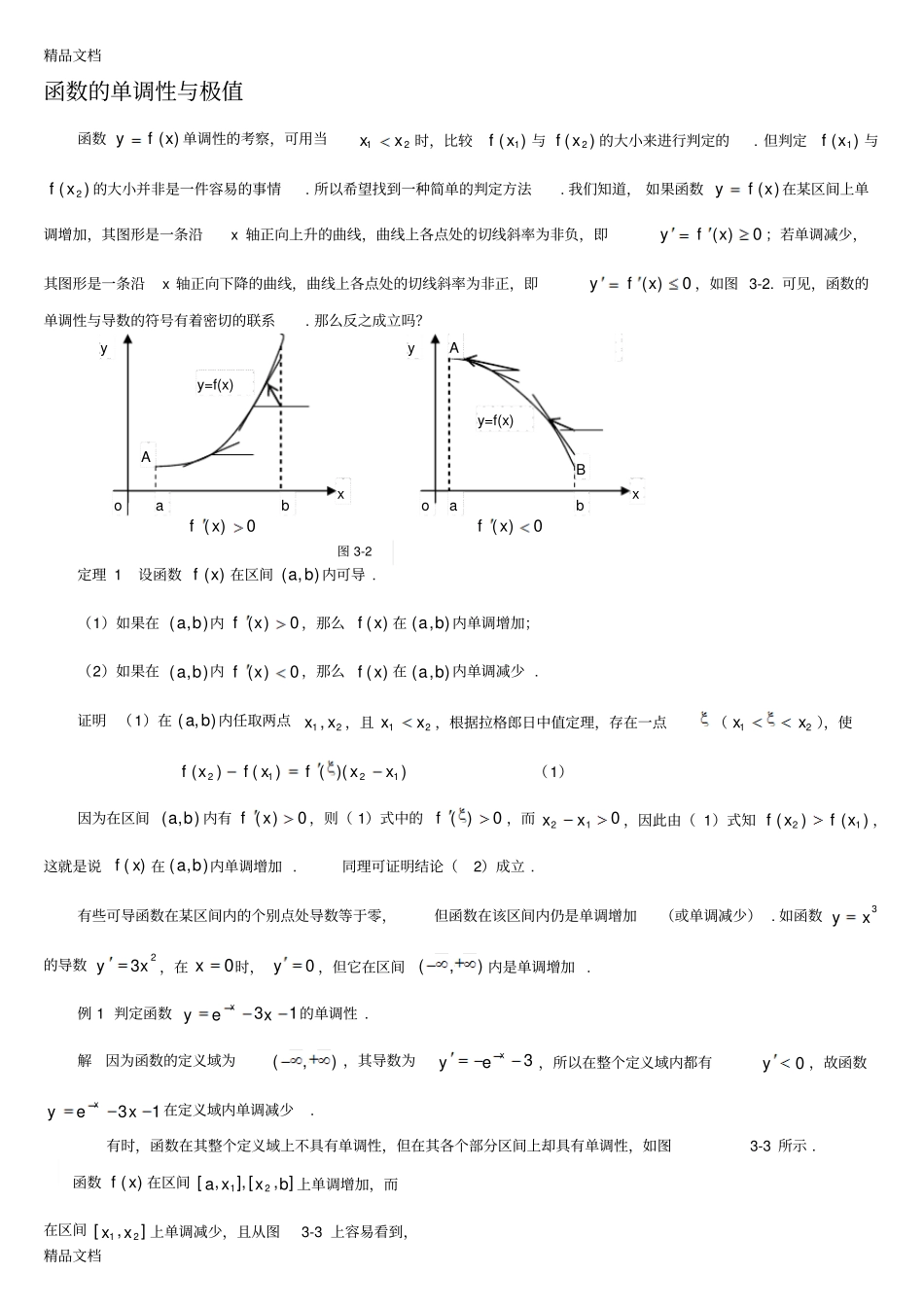
精品文档精品文档函数的单调性与极值函数)(xfy单调性的考察,可用当21xx时,比较)(1xf与)(2xf的大小来进行判定的.但判定)(1xf与)(2xf的大小并非是一件容易的事情.所以希望找到一种简单的判定方法.我们知道,如果函数)(xfy在某区间上单调增加,其图形是一条沿x轴正向上升的曲线,曲线上各点处的切线斜率为非负,即0)(xfy;若单调减少,其图形是一条沿x轴正向下降的曲线,曲线上各点处的切线斜率为非正,即0)(xfy,如图3-2.可见,函数的单调性与导数的符号有着密切的联系.那么反之成立吗?0)(xf0)(xf定理1设函数)(xf在区间),(ba内可导.(1)如果在),(ba内0)(xf,那么)(xf在),(ba内单调增加;(2)如果在),(ba内0)(xf,那么)(xf在),(ba内单调减少.证明(1)在),(ba内任取两点21,xx,且21xx,根据拉格郎日中值定理,存在一点(21xx),使))(()()(1212xxfxfxf(1)因为在区间),(ba内有0)(xf,则(1)式中的0)(f,而012xx,因此由(1)式知)()(12xfxf,这就是说)(xf在),(ba内单调增加.同理可证明结论(2)成立.有些可导函数在某区间内的个别点处导数等于零,但函数在该区间内仍是单调增加(或单调减少).如函数3xy的导数23xy,在0x时,0y,但它在区间),(内是单调增加.例1判定函数13xeyx的单调性.解因为函数的定义域为),(,其导数为3xey,所以在整个定义域内都有0y,故函数13xeyx在定义域内单调减少.有时,函数在其整个定义域上不具有单调性,但在其各个部分区间上却具有单调性,如图3-3所示.函数)(xf在区间],[],,[21bxxa上单调增加,而在区间],[21xx上单调减少,且从图3-3上容易看到,ABAyxoaby=f(x)yxoaby=f(x)图3-2精品文档精品文档可导函数)(xf在单调增加、减少的分界点处的导数为零,即0)()(21xfxf.使导数等于零的点(即方程0)(xf的实根),叫做函数)(xf的驻点.因此要确定可导函数)(xf的单调区间,首先要求出驻点,然后用这些驻点将其定义域分成若干个区间,再在每个区间上判定函数的单调性.例2讨论函数)(xfxxx2213123的单调性解因为)1)(2(2)(2xxxxxf,令0)(xf,得驻点1,221xx.这两点将)(xf的定义域),(分成三个部分:),1(),1,2(),2,(,下面用列表的形式来进行讨论,(表中“”表示单调增加,“”表示单调减少)x)2,(2()1,21),1()(xf+0--0+)(xf313651根据上面的讨论可得:函数)(xf在区间)2,(和),1(内单调增加,在区间()1,2内单调减少.另外,还需注意函数的不定义点,或是连续而不可导点也可能是单调区间的分界点.例3确定函数32xy的单调区间.解函数的定义域为),(,而332xy,显然当0x时,函数的导数不存在,又函数没有驻点.但当0x时,有0y,函数在区间),0(内单调增加;当0x时,有0y,函数在区间)0,(内单调减少.二、函数的极值定义3.1设函数)(xf在),(0xN有定义,且对此邻域内任一点x)(0xx均有)(xf)(0xf,则称)(0xf是函数)(xf的一个极大值;如果对此邻域内任一点x)(0xx均有)(xf)(0xf,则称)(0xf是函数)(xf的一个极小值.函数的极大值与极小值统称为函数的极值,使函数取得极值的点0x称为极值点.yxbaox1x2x3x图3-3xyo图3-4精品文档精品文档从图3-5可知,关于函数的极值,应注意以下几点:(1)函数的极大值和极小值是局部概念,即如果)(0xf是)(xf的极值,只是对极值点0x的左右近旁一个小范围来讲的.(2)函数在一个区间上可能会有几个极大值和几个极小值,且其中的极大值未必比极小值要大.如图3-5,极大值)(1xf就比极小值)(5xf还要小.(3)函数的极值只能在区间内部取到.求极值的关键是找出极值点,从图3-5中看到,对可导函数来讲,在取得极值处,曲线的切线是水平的,即在极值点处函数的导数为零.但反之不成立.如0)(3xf.定理2(极值存在的必要条件)设函数)(xf在点0x处导数存在,且在0x处取得极值,则函数)(xf在0x处的导数0)(0xf,即0x是函数)(xf的驻点.注意,定理3.5仅是极值存在的必要条件,而非充分条件.如函数3xy,在0x处有00xy,但00xy不是极值.该定理说明可导函数的极值点必是驻点,而驻点却未必是极值点.对于一个连续函数,它的极值点还可能是使导数不存在的点.如)(xf||x,显然,)0(f不存在.但0x且是它的一个极小值点,在||)(xxf图形上,)0,0(称为曲线的尖点.因此,连续函数有可能...