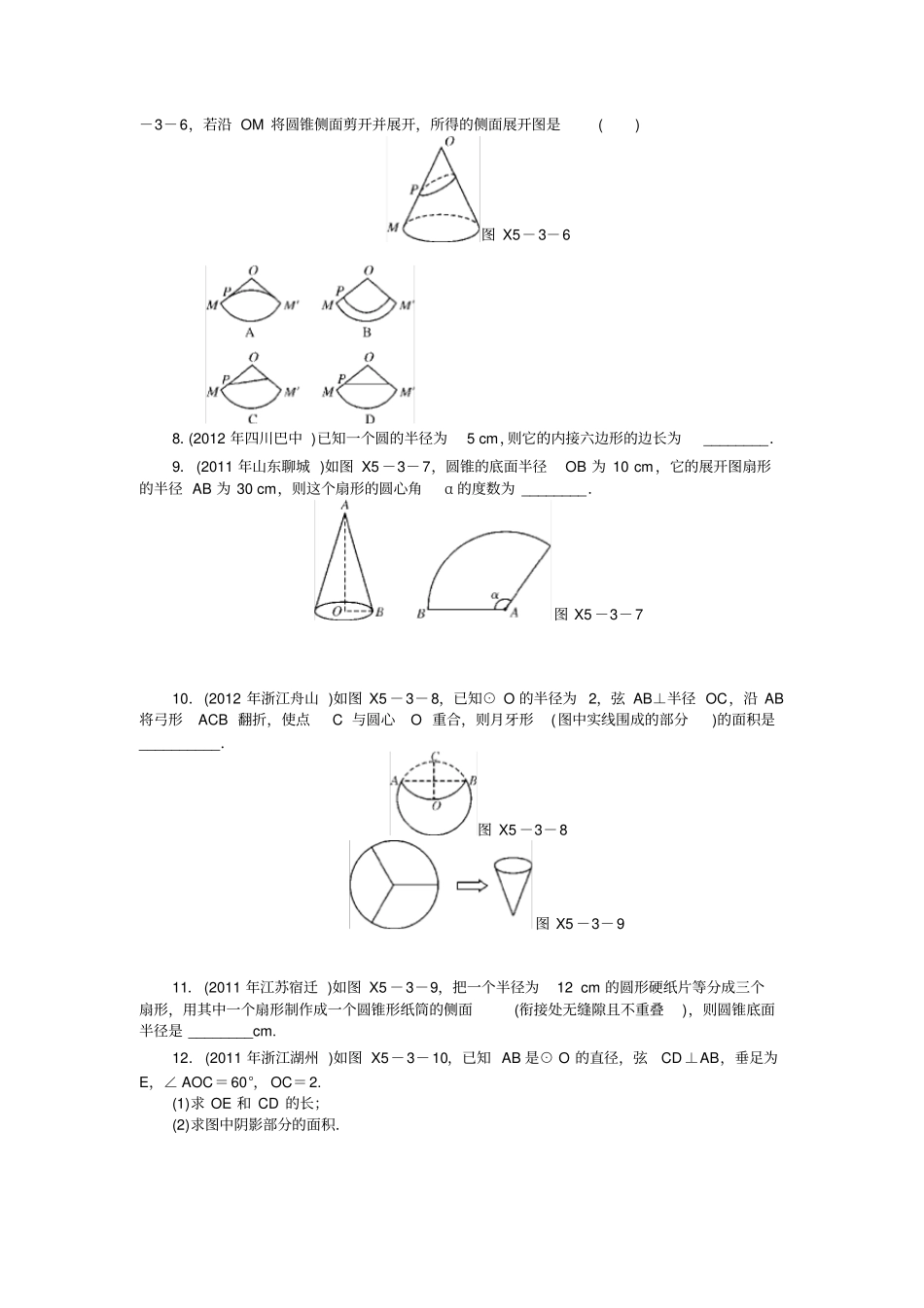
与圆有关的计算A级基础题1.(2012年湖南衡阳)一个圆锥的三视图如图X5-3-1,则此圆锥的底面积为()图X5-3-1A.30πcm2B.25πcm2C.50πcm2D.100πcm22.(2012年四川自贡)如图X5-3-2,圆锥形冰淇淋盒的母线长是13cm,高是12cm,则该圆锥形底面圆的面积是()图X5-3-2A.10πcm2B.25πcm2C.60πcm2D.65πcm23.如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”,则半径为2的“等边扇形”的面积为()A.πB.1C.2D.23π4.(2012年湖南娄底)如图X5-3-3,正方形MNEF的四个顶点在直径为4的大圆上,小圆与正方形各边都相切,AB与CD是大圆的直径,AB⊥CD,CD⊥MN,则图中阴影部分的面积是()A.4πB.3πC.2πD.π图X5-3-3图X5-3-45.(2012年福建漳州)如图X5-3-4,一枚直径为4cm的圆形古钱币沿着直线滚动一周,圆心移动的距离是()A.2πcmB.4πcmC.8πcmD.16πcm图X5-3-56.(2012年湖南衡阳)如图X5-3-5,⊙O的半径为6cm,直线AB是⊙O的切线,切点为B,弦BC∥AO.若∠A=30°,则劣弧的长为__________cm.7.(2011年内蒙古乌兰察布)已知O为圆锥的顶点,M为圆锥底面上一点,点P在OM上.一只蜗牛从点P出发,绕圆锥侧面爬行,回到点P时所爬过的最短路线的痕迹如图X5-3-6,若沿OM将圆锥侧面剪开并展开,所得的侧面展开图是()图X5-3-68.(2012年四川巴中)已知一个圆的半径为5cm,则它的内接六边形的边长为________.9.(2011年山东聊城)如图X5-3-7,圆锥的底面半径OB为10cm,它的展开图扇形的半径AB为30cm,则这个扇形的圆心角α的度数为________.图X5-3-710.(2012年浙江舟山)如图X5-3-8,已知⊙O的半径为2,弦AB⊥半径OC,沿AB将弓形ACB翻折,使点C与圆心O重合,则月牙形(图中实线围成的部分)的面积是__________.图X5-3-8图X5-3-911.(2011年江苏宿迁)如图X5-3-9,把一个半径为12cm的圆形硬纸片等分成三个扇形,用其中一个扇形制作成一个圆锥形纸筒的侧面(衔接处无缝隙且不重叠),则圆锥底面半径是________cm.12.(2011年浙江湖州)如图X5-3-10,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,OC=2.(1)求OE和CD的长;(2)求图中阴影部分的面积.图X5-3-10B级中等题13.某花园内有一块五边形的空地如图X5-3-11,为了美化环境,现计划在五边形各顶点为圆心,2m长为半径的扇形区域(阴影部分)种上花草,那么种上花草的扇形区域总面积是()A.6πm2B.5πm2C.4πm2D.3πm2图X5-3-11图X5-3-1214.(2012年四川凉山州)如图X5-1-12,在由小正方形构成的网格中,半径为1的⊙O在格点上,则图中阴影部分两个小扇形的面积之和为________________________________________________________________________(结果保留π).15.(2011年广东深圳)如图X5-3-13(1),已知在⊙O中,点C为劣弧AB上的中点,连接AC并延长至D,使CD=CA,连接DB并延长DB交⊙O于点E,连接AE.(1)求证:AE是⊙O的直径;(2)如图X5-3-13(2),连接EC,⊙O半径为5,AC的长为4,求阴影部分的面积之和(结果保留π与根号).(1)(2)图X5-3-13C级拔尖题16.(2011年四川广安)如图X5-3-14,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点,且PC=23BC.一只蚂蚁从点A出发,沿着圆柱体的表面爬行到点P的最短距离是()图X5-3-14A.cmB.5cmC.35cmD.7cm选做题17.(2012年湖南岳阳)如图X5-3-15,在⊙O中,,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.(1)求证:AC2=AB·AF;(2)若⊙O的半径长为2cm,∠B=60°,求图中阴影部分的面积.图X5-3-1564π与圆有关的计算1.B2.B3.C解析: 半径为2,弧长为2,则S扇形=12×2×2=2.4.D5.B6.2π7.D8.5cm9.120°10.4π3+2311.412.解:(1)在△OCE中, ∠CEO=90°,∠EOC=60°,OC=2,∴OE=12OC=1.∴CE=32OC=3. OA⊥CD,∴CE=DE.∴CD=23.(2) S△ABC=12AB·EC=12×4×3=23,∴S阴影=12π×22-23=2π-23.13.A14.π415.(1)证明:连接CE. 点C为劣弧AB上的中点,∴CE平分∠AED. CD=CA,∴△ADE为等腰三角形.∴CE⊥AD.∴AE是⊙O的直径.(2)解:由(1)可知,AE是⊙O的直径,∴...