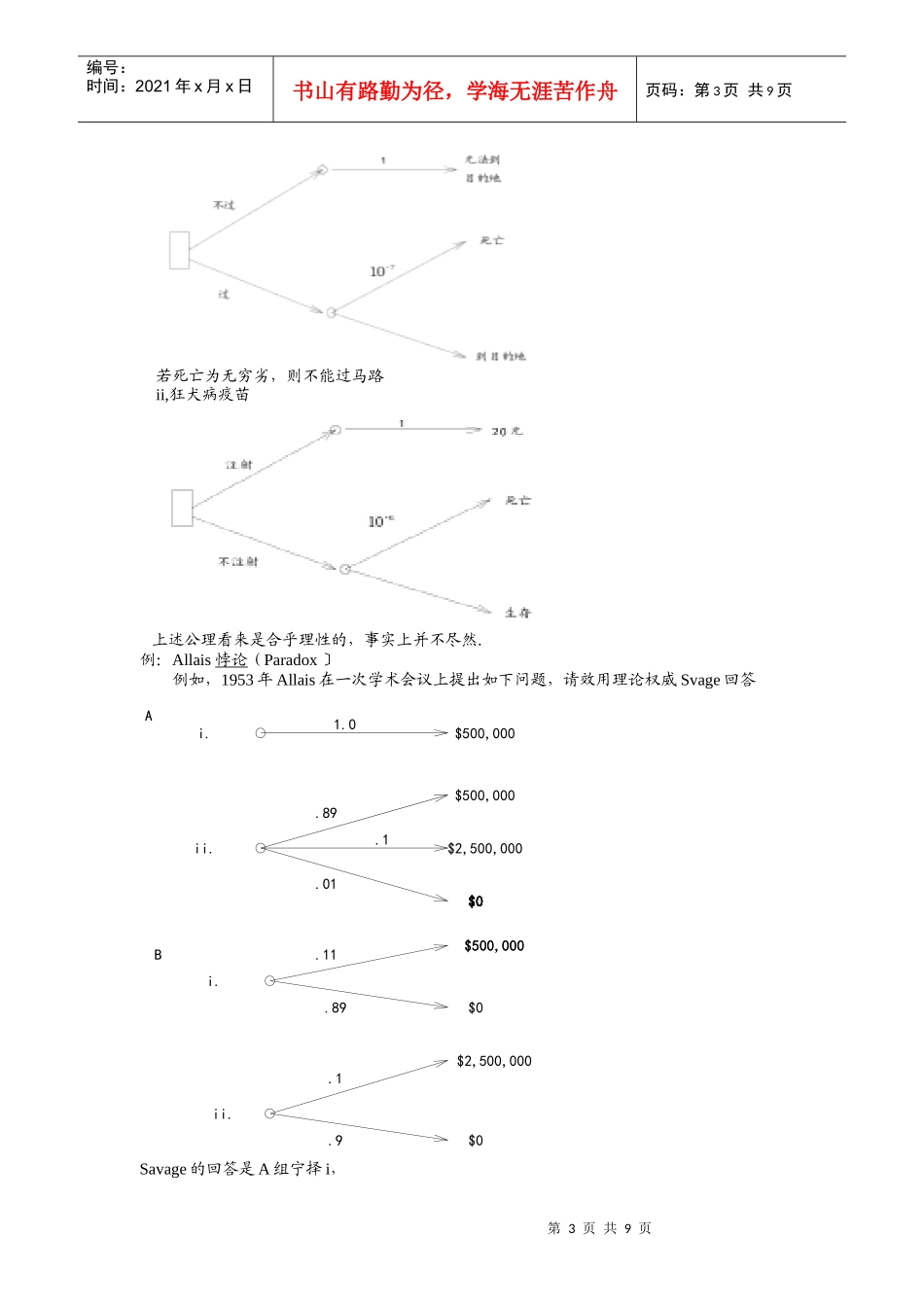
第1页共9页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第1页共9页第三章效用、损失和风险(Utility,LossandRisk)本章主要参考文献:60,56,86,87,92,129,156,169,183,184§3—1效用的定义和公理系统一、引言·为什么要引入效用决策问题的特点:自然状态不确定——以概率表示;后果价值待定:以效用度量。1.无形后果,非数字量(如信誉、威信、出门带伞问题的后果)需以数值度量;2.即使是数值量(例如货币)表示的后果,其价值仍有待确定,后果的价值因人而异。例一:同是100元钱,对穷人和百万富翁的价值绝然不同;对同一个人,身无分文时的100元,与已有10000元再增加100元的作用不同,这是钱的边缘价值问题。例二:上图作为商业、经营中实际问题的数学模型有普遍意义有人认为打赌不如礼品,即*由上面两个例子可知:在进行决策分析时,存在如何描述(表达)后果的实际价值,以便反映决策的人偏好次序(preferenceorder)的问题*偏好次序是决策人的个性与价值观的反映,与决策人所处的社会、经济地位,文化素养,心理和生理(身体)状态有关。*除风险偏好之外,还时间偏好。i,折扣率ii,其他而效用(Utility)就是偏好的量化,是数(实值函数).DanielBernoulli在1738年指出:若一个人面临从给定行动集(风险性展望集)中作选择的决策问题,如果他知道与给定行动有关的将来的自然状态,且这些状态出现的概率已知或可以估计,则他应选择对各种可能后果的偏好的期望值最高的行动。二、效用的定义1.符号i,AB(即APB)读作A优于B:(Prefer(ed)AtoB)AB(即ARB)A不劣于B礼品抽奖10.50.51000元02500元1000元优于02500元0.50.5第2页共9页第1页共9页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第2页共9页A~B(即AIB)A无差别于B(Indifference)ii,展望(prospect):可能的前景即各种后果及后果出现概率的组合P=(……)既考虑各种后果(consequence)又考虑了各种后果的概率(probabilityorlikelihood)分布所有P的集合记作piii,抽奖(lottery)与确定当量若(;)则称确定性后果为抽奖(;)的确定当量2.效用的定义(A)在集合p上的实值函数u,若它和p上的优先关系一致,即:若p,iffu()≥u()则称u为效用函数三、效用存在性公理理性行为公理VonNeumann-Morenstern,1994[169]·公理1连通性(Connectivity)又称可比性p,则oror·公理2传递性(Transitivity)p,若,则·公理3替代性公理(加等量时优先关系不变)若p,且01则对任何∈p,必有+(1-)+(1-)或者表达成:,则+(1-)+(1-)即二种后果中,决策人所偏好的后果出现机会较大的情况是决策人所喜爱的。·公理4连续性公理----偏好的有界性若则存在01,01,使+(1-)+(1-)由+(1-)可知不是无穷劣,即u()由+(1-)可知不是无穷优,即u()即使是死亡,亦不至于无穷劣例:i,过马路第3页共9页第2页共9页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第3页共9页若死亡为无穷劣,则不能过马路ii,狂犬病疫苗上述公理看来是合乎理性的,事实上并不尽然.例:Allais悖论(Paradox〕例如,1953年Allais在一次学术会议上提出如下问题,请效用理论权威Svage回答Savage的回答是A组宁择i,i.ABi.ii.ii.$2,500,000$500,000$500,000$0$0$0$0$0$0$0$0$500,000$500,000$2,500,0001.0.89.1.01.11.89.1.9第4页共9页第3页共9页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第4页共9页B组宁择ii,Allais指出:B组的i,ii,均以0.89的$500,000取代0.89的$0,即与A组的i,ii,相对应,照公理3、A、B两组中i,ii,的优先关系应当不变。Savage当时语塞。·效用的公理化定义在上述公理系统中,若p上存在实值函数u,使i,当且仅当u()>u()ii.u(α,;1-α,)=αu()+(1-α)u()iii,对满足上述条件的,必有()=b()+c,其中b,c∈,b>0则u(P)称为(基数)效用函数*关于线性:将ii.u(α,;1-α,)=αu()+(1-α)u()推广到一般,若∈p;≥0,i=1,2,…m;=1;则u()=u()四、基数效用与序数效用(Cardinal&OrdinalUtility)基数:实数:1,2,3,π序数:第一,二,…,4,...