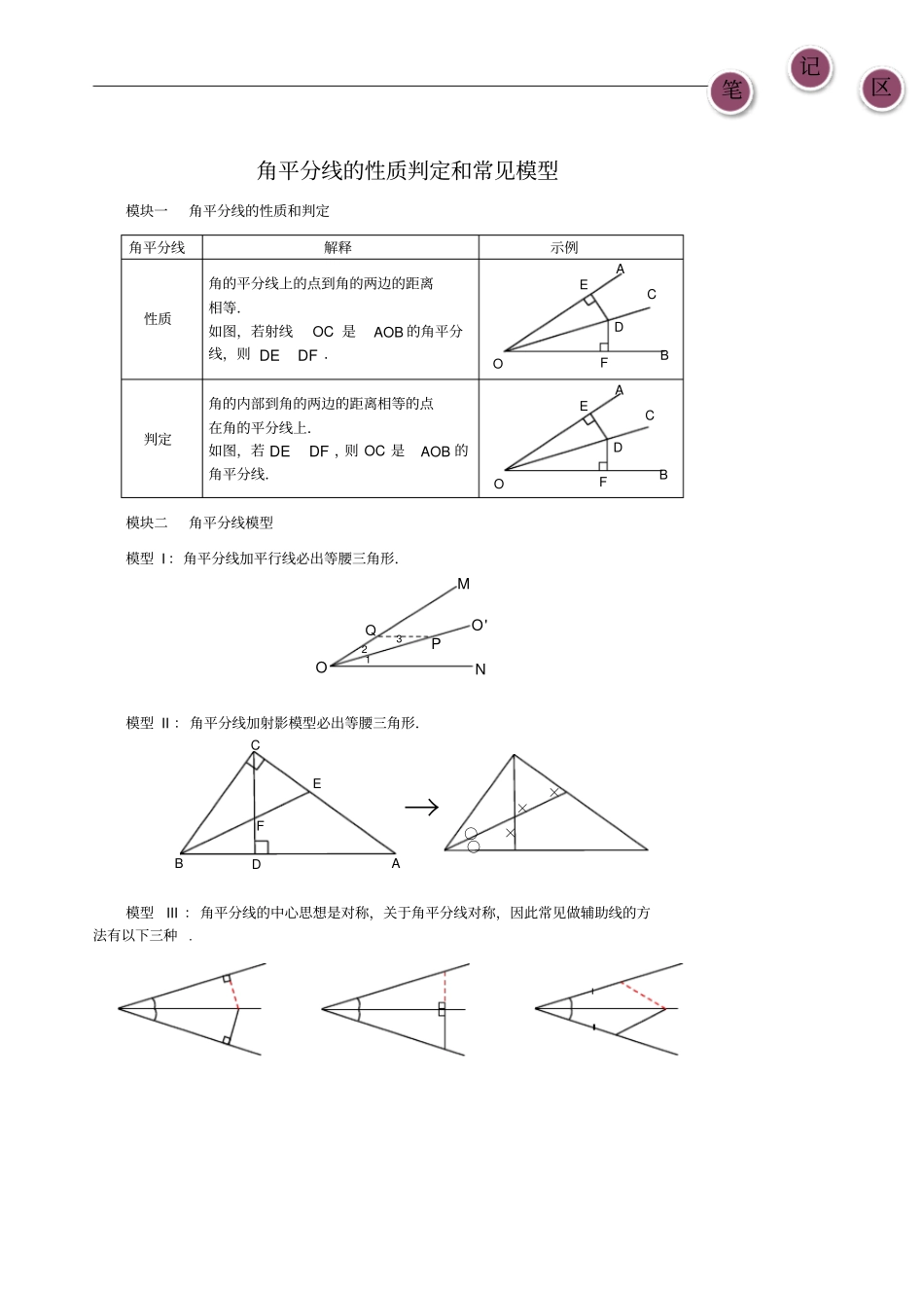
笔记区角平分线的性质判定和常见模型模块一角平分线的性质和判定角平分线解释示例性质角的平分线上的点到角的两边的距离相等.如图,若射线OC是AOB的角平分线,则DEDF.判定角的内部到角的两边的距离相等的点在角的平分线上.如图,若DEDF,则OC是AOB的角平分线.模块二角平分线模型模型I:角平分线加平行线必出等腰三角形.模型II:角平分线加射影模型必出等腰三角形.→模型III:角平分线的中心思想是对称,关于角平分线对称,因此常见做辅助线的方法有以下三种.DFEOCBADFEOCBAFABCDE××○○×MQ'OONP123笔记区(1)如图,在ABC△中,90C,AD是角平分线,DEAB,3cmDE,5cmBD,则BC__________.(2)(14—15年嘉祥期末)在ABC△中,90BAC,3AB,4AC,5BC,若点P是ABC△的三条角平分线的交点,则点P到边BC的距离是_____________.【解析】(1)8cm;(2)1(提示:过点P作三边的垂线,利用面积进行求解).【教师备课提示】这道题主要讲解角平分线的性质.(1)证明:三角形三个角的角平分线交于一点.(2)(14年—15年金牛区期末)如图,ABC△的外角一平分线CP和内角平分线BP相交于点P,若=80BAC,则=CAP____________.【解析】(1)如图,在ABC△中,设BAC、ABC的平分线的交点为I,过I点作IDAB于D,IEAC于E,IFBC于F,连接IC. AI、BI都是角平分线,∴IDIE,IDIF,∴IEIF,∴CI是ACB的平分线,∴三角形三个角的平分线交于一点.(2)50°(提示:过点P向三边作垂线,证明AP是BAC的外交角平分线)【教师备课提示】这道题主要讲解角平分线的判定,结合角平分线的性质.模块一角平分线的性质和判定例题1例题2IFEDCBA第19题CAEDBBABPCD笔记区(1)如图3-1,在ABC△中,BD、CD分别平分ABC和ACB,//EDAB,//FDAC.如果6BC,则DEF△的周长为__________.(2)(14—15年武侯区期末)如图3-2,ABC的平分线与ACB的外角平分线相交于点D,过点D作EF//BC,交AB于E,交AC于F,若8cmBE,5cmCF,则EF________.(3)(15—16年武侯期末)如图3-3,ABC△的内角ABC∠和外角ACD∠的平分线相交于点E,BE交AC于点F,过点E作EG//BD交AB于点G,交AC于点H,连接AE,有以下结论:①12BECBAC∠∠;②HEFCBF△≌△;③BGCHGH;④AEBACE∠∠90,其中正确的结论有_____________(只填序号)图3-1图3-2图3-3【解析】(1)6;(2)3cm;(3)①③④.【教师备课提示】这道题主要讲解角平分线加平行线必出等腰三角形的模型.(1)(14—15年青羊区期末)如图4-1,在ABC△中,90BAC,ADBC于点D,ABC的平分线BE交AD于F,交AC于E,若3AE,2DF,则AD_____________.(2)如图4-2,已知:在ABC△中,90BAC,ADBC于D,BCA的角平分线交AD与F,交AB于E,//FGBC交AB于G.4cmAE,12cmAB,则BG__________,GE__________.图4-1图4-2模块二角平分线模型例题3例题4HFGABCDEBAEFCDABCGDFEABFEDCABDCFEG笔记区【解析】(1)5;(2)4cm;4cm.过E作EH垂直BC交BC于H点,易证AECEHC△≌△;由角度分析易知AEFAFE,即AEAF,则有EHEAAF;又可证AGFBHE△≌△,则1248AGEB,则844BG,4GE.【教师备课提示】这道题主要讲解角平分线加射影模型必出等腰三角形的模型.如图,在ABC△中,12,2ABAC,ADBD.求证:DCAC.【解析】过D作DEAB于MON, ADBD,DEAB,∴ADEBDE△≌△,∴12AEBEABAC, 12,∴ADEADC△≌△,∴90ACDAED,∴DCAC.【教师备课提示】这道题主要讲解角平分线第一种辅助线.如图所示,在ABC△中,90BAC,ABAC,BE平分ABC,CEBE.求证:12CEBD.例题5例题6ABDCFEGHABDC12ABDC12EBACEDBACEDF123笔记区【解析】延长CE、BA相交于F,在BEC△和BEF△中,12BEBEBEFBEC∴BECBEF△≌△∴12CEEFCF BECE,∴190F同理390F,∴13在ABD△和ACF△中,13ABACBADCAF∴ABDACF△≌△∴BDCF,∴12CEBD.【教师备课提示】这道题主要讲解角平分线的第二种辅助线.(14—15年嘉祥月考)如图,在ABC△中,60ABC,AD、CE分别平分BAC、ACB,AD、CE交于O.(1)求AOC的度数;(2)求证:ACAECD.【解析】(1)=120AOC;(2)在AC上截取AT,使ATAE,连接OT,在AOE△和AOT△中,ATAEOATOAEAOAO∴(SAS)AOEAOT△≌△,∴60AOTAOE,∴60COTCOD在COT...