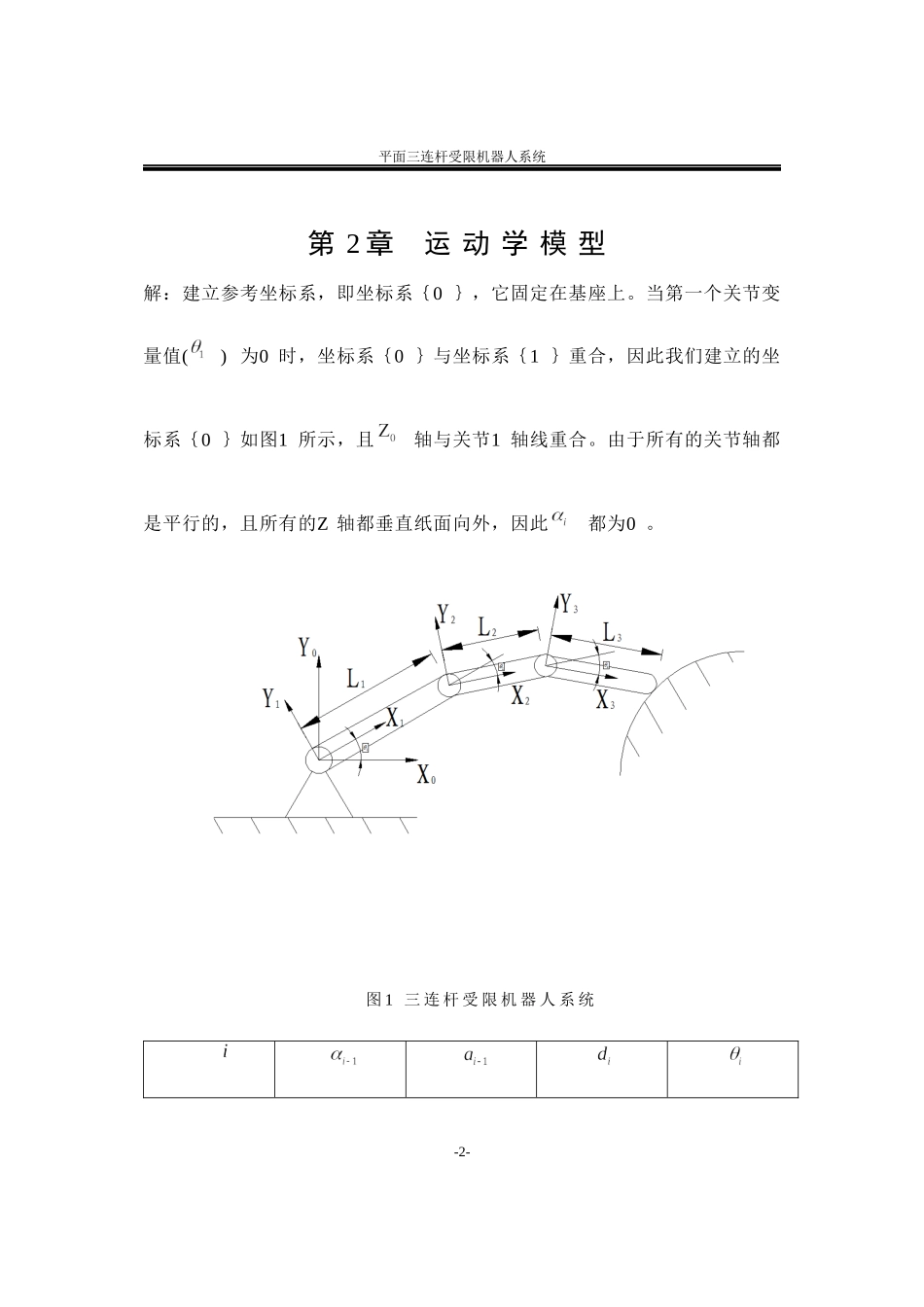
平面三连杆受限机器人系统第1章概述如图1所示为一个平面三连杆受限机器人系统。因为三个关节均为转动关节,因此有时称该操作臂为RRR机构。在此机构上建立连杆坐标系,并求:(1)运动学模型(2)动力学模型1平面三连杆受限机器人系统第2章运动学模型解:建立参考坐标系,即坐标系{0},它固定在基座上。当第一个关节变量值()为0时,坐标系{0}与坐标系{1}重合,因此我们建立的坐标系{0}如图1所示,且轴与关节1轴线重合。由于所有的关节轴都是平行的,且所有的Z轴都垂直纸面向外,因此都为0。图1三连杆受限机器人系统--21000200300图2三连杆平面操作臂的连杆参数表(1)(2)(3)3平面三连杆受限机器人系统(4)式中(5)(6)当{G}={T}时,有(7)因此(8)--4第3章动力学模型本文同时假设连杆1、2、3的单位长度的均匀质量密度分别为、和,且始终在约束面上移动。建立如图3所示的平面惯性笛卡尔坐标系,(X,Y)表示该坐标系的坐标变量.本文忽略连杆3末端与约束面之间的摩擦并假设该平面三连杆受限机器人的系统约束为一完整约束,即只与位置变量有关而与速度变量无关,利用连杆3末端的位置向量=可将约束面表示为=0(9)本文假设连杆1、2和3均为刚性杆,故不会产生任何变形。连杆3末端的位置向量=的各分量可表示为(10)(11)将其代入式(1)可得(12)5平面三连杆受限机器人系统图3平面三连杆受限机器人对于连杆1、2和3,由图3所示的坐标系可知其上任意一点的坐标向量分别为(13)(14)(15)式中,、、分别表示连杆1、2和3任意一点的坐标向量。--11111cossinxrx112222122coscossinsinLxrLx1122333112233coscoscossinsinsinLLxrLLx63.1总动能T由图3所示的坐标系可得该机器人系统的总动能T的表达式为(16)将式(1)(7)代入(8),有(17)式中,(18)于是有:7平面三连杆受限机器人系统(19)3.2轴向压力令是与约束面的约束方程即式(9)或(12)相对应的Lagrange算子,由于机器人在工作过程中要求终端执行机构在约束面上运动,必然会在约束面和执行机构之间产生一个在约束面的法向方向矢量n上的反作用力Fn,容易得到(20)因为轴向压力是在轴的单位向量上的正交映射,故可表示为(21)式中,=,是轴上的单位向量。--83.3总势能V对于本文所研究的机器人系统,其总势能为(22)式中:为连杆重力所引起的重力势能。连杆3引起的可以分别表示为(23)9