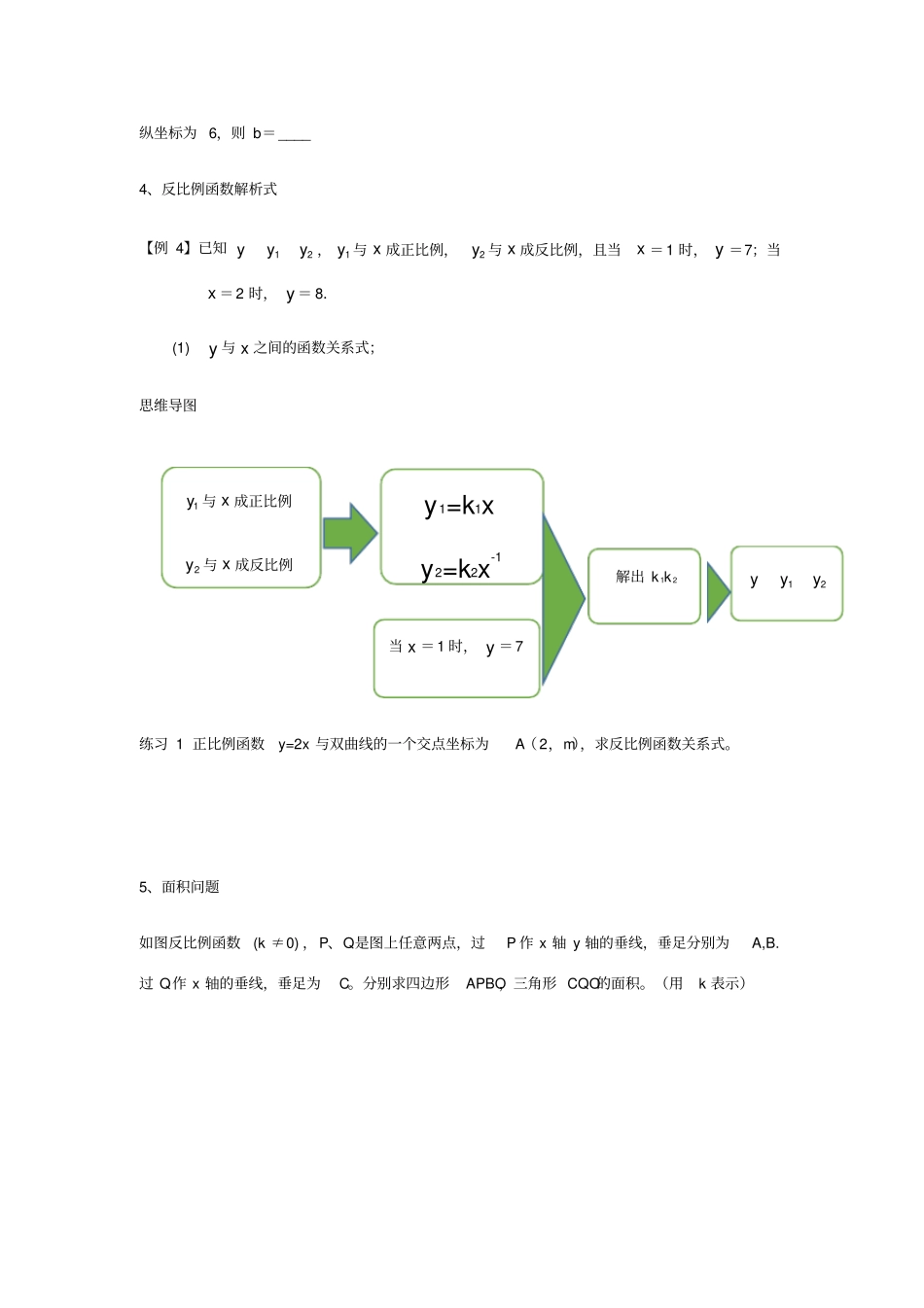
【例1】如果函数222kkkxy的图像是双曲线,且在第二,四象限内,那么K的值是多少?函数的解析式?思维导图练习1当k为何值时22(1)kykx是反比例函数?练习2.已知y=(a﹣1)是反比例函数,则a=.练习3.如果函数y=(k+1)是反比例函数,那么k=.练习4.如果函数y=x2m﹣1为反比例函数,则m的值是2.增减性问题【例2】在反比例函数xy1的图像上有三点1x,1y,2x,2y,3x,3y。若3210xxx则下列各式正确的是()A.213yyyB.123yyyC.321yyyD.231yyy思维导图双曲线K≠02K2+K-2=-1二,四象限K<0K=-1练习1.若A(-3,y1),B(-2,y2),C(-1,y3)三点都在函数y=-x1的图象上,则y1,y2,y3的大小关系是().A.y1>y2>y3<y2<y3=y2=y3<y3<y2练习2.已知反比例函数y=xm21的图象上有A(x1,y1)、B(x2,y2)两点,当x1<x2<0时,y1<y2,则m的取值范围是().A.m<0>0<21>3、交点问题【例3】如果一次函数的图像与反比例函数xmnymnmxy30相交于点(221,),那么该直线与双曲线的另一个交点为()思维导图练习1,若反比例函数y=xb3和一次函数y=3x+b的图象有两个交点,且有一个交点的交点(21,2)在联立两个函数即可求解分别代入两个函数得到方程组解出m,nK=-1<0Y1>y2<0函数在二四X1>X2>0213yyy纵坐标为6,则b=____4、反比例函数解析式【例4】已知12yyy,1y与x成正比例,2y与x成反比例,且当x=1时,y=7;当x=2时,y=8.(1)y与x之间的函数关系式;思维导图练习1正比例函数y=2x与双曲线的一个交点坐标为A(2,m),求反比例函数关系式。5、面积问题如图反比例函数(k≠0),P、Q是图上任意两点,过P作x轴y轴的垂线,垂足分别为A,B.过Q作x轴的垂线,垂足为C。分别求四边形APBO,三角形CQO的面积。(用k表示)1y与x成正比例2y与x成反比例y1=k1xy2=k2x-1解出k1k212yyy当x=1时,y=7思维导图三角形CQO的面积的求法同上。练习1如图,在AOBRt中,点A是直线mxy与双曲线在第一象限的交点,且,则的值是_____.练习2已知点A(0,2)和点B(0,-2),点P在函数1yx的图象上,如果△PAB的面积是6,求P点的坐标.SAPBO=AP×BO设P点坐标(x,y)SAPBO=lxl×lyl图形过二四象限SAPBO=-k1.点A(-2,y1)与点B(-1,y2)都在反比例函数y=-的图像上,则y1与y2的大小关系为()<y2>y2=y2D.无法确定2.若点(3,4)是反比例函数y=221mmx图象上一点,则此函数图象必经过点()A.(2,6)B.(2,-6)C.(4,-3)D.(3,-4)3.在函数y=,y=x+5,y=-5x的图像中,是中心对称图形,且对称中心是原点的图像的个数有()4.已知函数y=kx(k<0),又x1,x2对应的函数值分别是y1,y2,若x2>x1>0对,则有()>y2>0>y1>0<y2<0<y1<05.如图1,函数y=a(x-3)与y=ax,在同一坐标系中的大致图象是()图1oyxyxoyxoyxoABCD6.若y与x成反比例,x与z成正比例,则y是z的()A、正比例函数B、反比例函数C、一次函数D、不能确定7.如果矩形的面积为6cm2,那么它的长ycm与宽xcm之间的函数图象大致为()8.(2014山东青岛一模)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应()A、不小于54m3B、小于54m3C、不小于45m3D、小于45m39.如图,A、C是函数的图象上的任意两点,过A作轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记RtΔAOB的面积为S1,RtΔCOD的面积为S2则()>S2B.S1