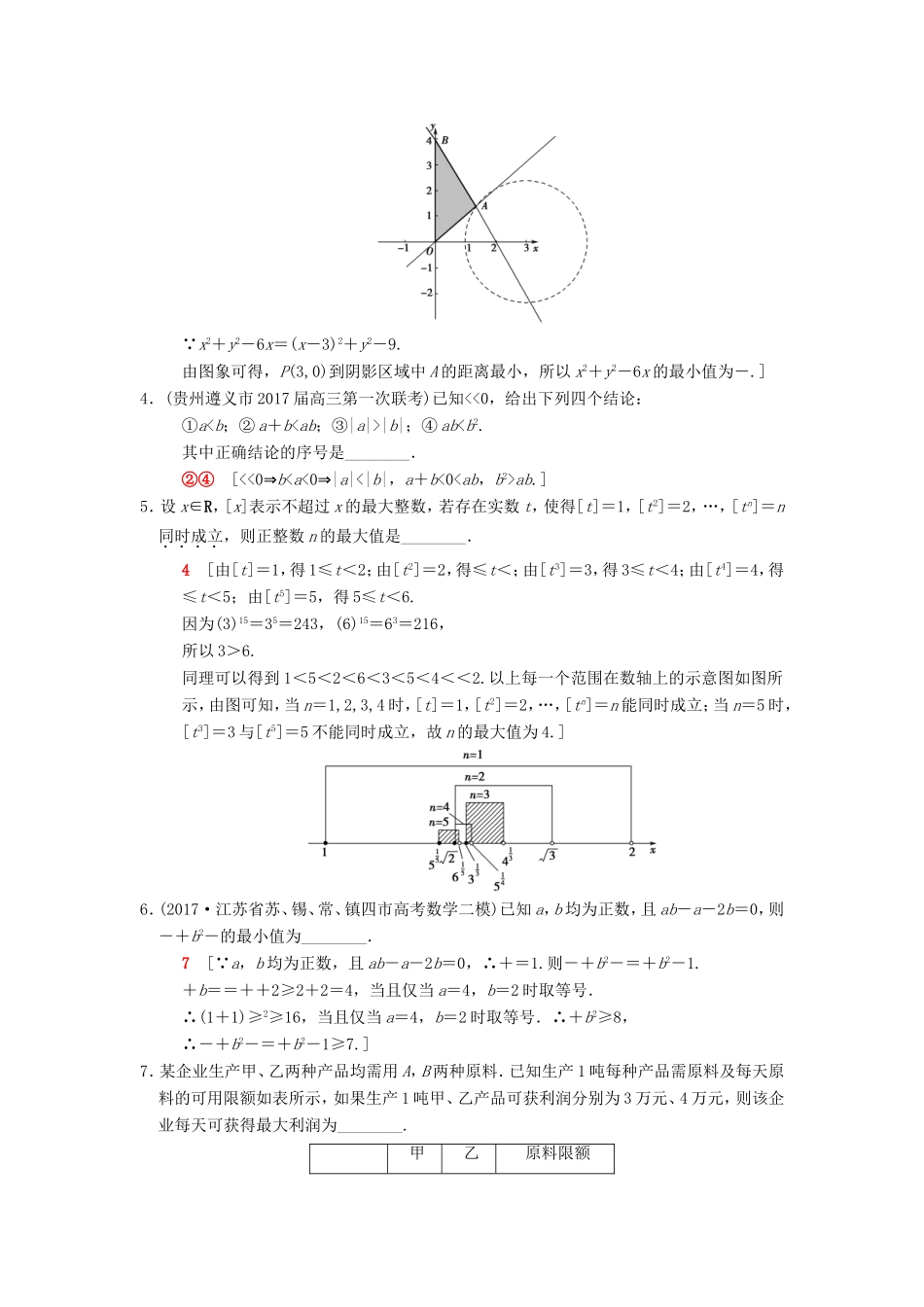
专题限时集训(七)不等式(对应学生用书第95页)(限时:120分钟)一、填空题(本大题共14小题,每小题5分,共70分,请把答案填写在题中横线上.)1.(江苏省泰州中学2017届高三上学期第二次月考)设实数x,y满足约束条件则z=2x+3y的最大值为________.【导学号:56394049】26[作出不等式对应的平面区域(阴影部分),由z=2x+3y,得y=-x+,平移直线y=-x+,由图象可知当直线y=-x+经过点A时,直线y=-x+的截距最大,此时z最大.由解得即A(4,6).此时z的最大值为z=2×4+3×6=26.]2.(无锡市普通高中2017届高三上学期期中基础性检测)已知正实数x,y满足+2y-2=lnx+lny,则xy=________.[由题设可得lnxy=+2y-2≥2-2(当且仅当x=4y时取等号),即lnxy≥2-2,也即⇒所以xy=.]3.(江苏省镇江市丹阳高中2017届高三下学期期中)已知动点P(x,y)满足:则x2+y2-6x的最小值为________.-[由(-x)(+y)≥1, y+>y+|y|≥0,∴-x≥=-y, 函数f(x)=-x=是减函数,∴x≤y,∴原不等式组化为该不等式组表示的平面区域如下图阴影部分所示: x2+y2-6x=(x-3)2+y2-9.由图象可得,P(3,0)到阴影区域中A的距离最小,所以x2+y2-6x的最小值为-.]4.(贵州遵义市2017届高三第一次联考)已知<<0,给出下列四个结论:①a
|b|;④abab.]5.设x∈R,[x]表示不超过x的最大整数,若存在实数t,使得[t]=1,[t2]=2,…,[tn]=n同时成立,则正整数n的最大值是________.4[由[t]=1,得1≤t<2;由[t2]=2,得≤t<;由[t3]=3,得3≤t<4;由[t4]=4,得≤t<5;由[t5]=5,得5≤t<6.因为(3)15=35=243,(6)15=63=216,所以3>6.同理可以得到1<5<2<6<3<5<4<<2.以上每一个范围在数轴上的示意图如图所示,由图可知,当n=1,2,3,4时,[t]=1,[t2]=2,…,[tn]=n能同时成立;当n=5时,[t3]=3与[t5]=5不能同时成立,故n的最大值为4.]6.(2017·江苏省苏、锡、常、镇四市高考数学二模)已知a,b均为正数,且ab-a-2b=0,则-+b2-的最小值为________.7[ a,b均为正数,且ab-a-2b=0,∴+=1.则-+b2-=+b2-1.+b==++2≥2+2=4,当且仅当a=4,b=2时取等号.∴(1+1)≥2≥16,当且仅当a=4,b=2时取等号.∴+b2≥8,∴-+b2-=+b2-1≥7.]7.某企业生产甲、乙两种产品均需用A,B两种原料.已知生产1吨每种产品需原料及每天原料的可用限额如表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为________.甲乙原料限额Α(吨)3212Β(吨)12818万元[设该企业每天生产甲、乙两种产品分别为x、y吨,则利润z=3x+4y.由题意可列其表示如图阴影部分区域:当直线3x+4y-z=0过点A(2,3)时,z取得最大值,所以zmax=3×2+4×3=18.]8.不等式|x-1|-|x-5|<2的解集是________.{x|x<4}[原不等式同解于如下三个不等式解集的并集;(Ⅰ)(Ⅱ)(Ⅲ)解(Ⅰ)得:x<1,解(Ⅱ)得:1≤x<4,解(Ⅲ)得:x∈∅,所以,原不等式的解集为{x|x<4}.]9.(江苏省南京市、盐城市2017届高三第一次模拟)在△ABC中,A,B,C所对的边分别为a,b,c,若a2+b2+2c2=8,则△ABC面积的最大值为________.[S△ABC=absinC=ab==,而2ab≤a2+b2=8-2c2⇒ab≤4-c2,所以S△ABC≤=≤×=,当且仅当a=b,c2=时取等号.]10.(河南省豫北名校联盟2017届高三年级精英对抗赛)已知当-1≤a≤1时,x2+(a-4)x+4-2a>0恒成立,则实数x的取值范围是________.(-∞,1)∪(3,+∞)[设f(a)=(x-2)a+(x2-4x+4),则f(a)>0对∀a∈[-1,1]成立等价于即解之得x<1或x>3,即实数x的取值范围是(-∞,1)∪(3,+∞).]11.(江苏省南京市2017届高考三模)已知a,b,c为正实数,且a+2b≤8c,+≤,则的取值范围为________.【导学号:56394050】[27,30][ a+2b≤8c,+≤,∴设x=,y=,则有∴作出平面区域如图所示:令z==3x+8y,则y=-x+,由图象可知当直线y=-x+经过点A时,截距最大,则z最大;当直线y=-x+与曲线y=相切时,截距最小,即z最小...