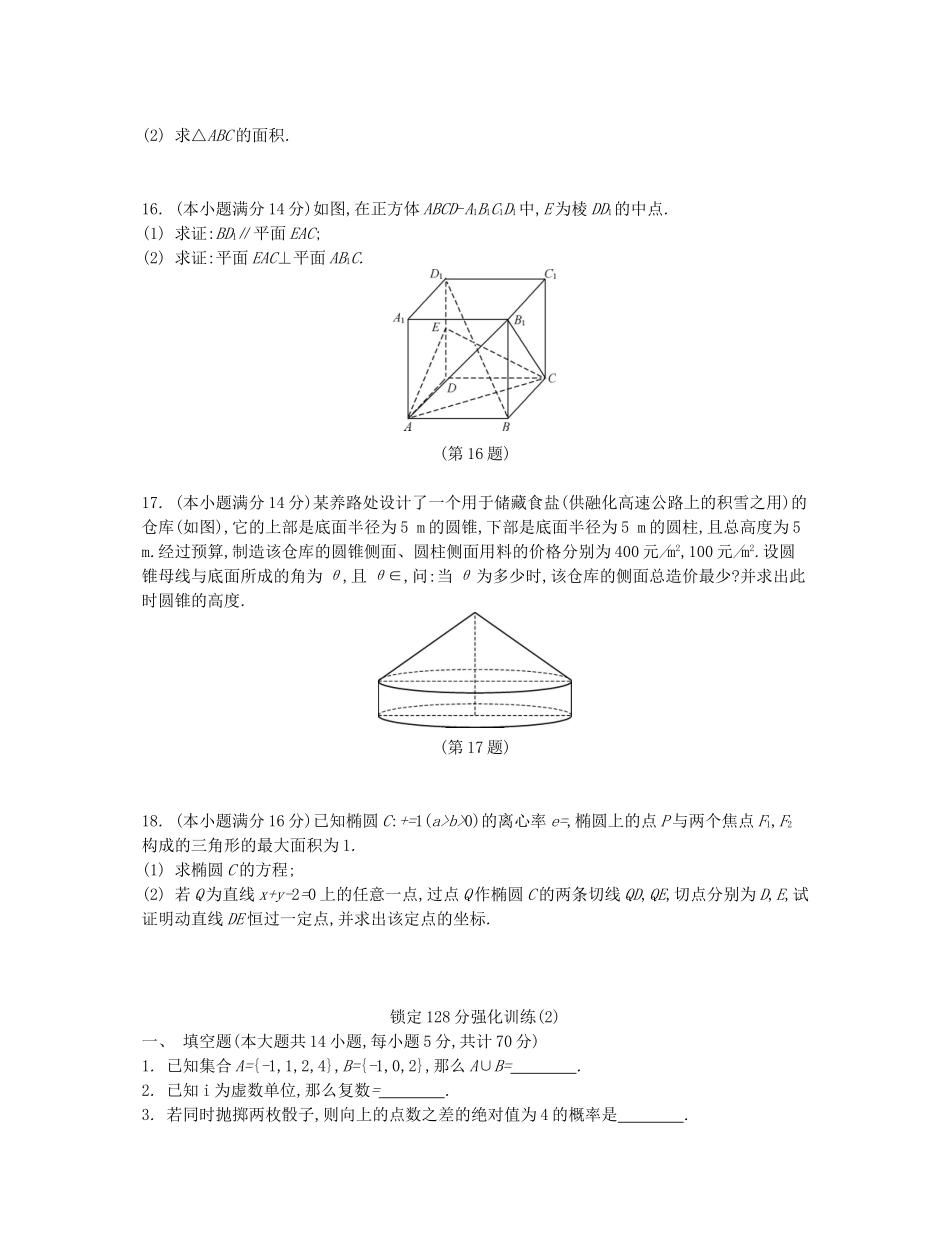
锁定128分强化训练(1)一、填空题(本大题共14小题,每小题5分,共计70分)1.已知全集U={1,2,3,4,5,6},集合A={2,3,5},B={1,3,4},那么A∩(∁UB)=.2.某校高一、高二、高三年级的学生人数分别是400,320,280.现采用分层抽样的方法抽取50人,参加学校举行的社会主义核心价值观知识竞赛,则样本中高三年级的人数是.3.若a+bi=(i是虚数单位,a,b∈R),则ab=.4.若在区间[20,80]内任取一个实数m,则实数m落在区间[50,75]内的概率为.5.函数f(x)=lg(-x2+x+2)的定义域为.6.已知实数x,y满足约束条件则z=3x-2y的最小值是.7.执行如图所示的流程图,如果输入的N的值为6,那么输出的p的值是.(第7题)8.若函数f(x)=Asin(A>0,ω>0)的图象如图所示,则函数f(x)在(0,π)内的零点为.(第8题)9.若高为4,底面边长为2的正四棱锥的顶点都在同一个球面上,则该球的体积为.10.如果将直线l:x+2y+c=0先向左平移1个单位长度,再向下平移2个单位长度后,所得的直线l'与圆C:x2+y2+2x-4y=0相切,则实数c的值构成的集合为.11.已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),若f(-1)>-2,f(-7)=,则实数a的取值范围为.12.已知M为双曲线C:-=1(a>0,b>0)右支上的一点,A,F分别为双曲线C的左顶点和右焦点,且△MAF为等边三角形,则双曲线C的离心率为.13.已知正数x,y满足2xy=,那么y的最大值为.14.已知两个等比数列{an},{bn}满足a1=a(a>0),b1-a1=1,b2-a2=2,b3-a3=3.若数列{an}唯一,则实数a的值为.题号1234567答案题号891011121314答案二、解答题(本大题共4小题,共58分,解答时应写出必要的文字说明、证明过程或演算步骤)15.(本小题满分14分)在△ABC中,角A,B,C所对的边分别为a,b,c.已知a=3,cosA=,B=A+.(1)求b的值;(2)求△ABC的面积.16.(本小题满分14分)如图,在正方体ABCD-A1B1C1D1中,E为棱DD1的中点.(1)求证:BD1∥平面EAC;(2)求证:平面EAC⊥平面AB1C.(第16题)17.(本小题满分14分)某养路处设计了一个用于储藏食盐(供融化高速公路上的积雪之用)的仓库(如图),它的上部是底面半径为5m的圆锥,下部是底面半径为5m的圆柱,且总高度为5m.经过预算,制造该仓库的圆锥侧面、圆柱侧面用料的价格分别为400元/m2,100元/m2.设圆锥母线与底面所成的角为θ,且θ∈,问:当θ为多少时,该仓库的侧面总造价最少?并求出此时圆锥的高度.(第17题)18.(本小题满分16分)已知椭圆C:+=1(a>b>0)的离心率e=,椭圆上的点P与两个焦点F1,F2构成的三角形的最大面积为1.(1)求椭圆C的方程;(2)若Q为直线x+y-2=0上的任意一点,过点Q作椭圆C的两条切线QD,QE,切点分别为D,E,试证明动直线DE恒过一定点,并求出该定点的坐标.锁定128分强化训练(2)一、填空题(本大题共14小题,每小题5分,共计70分)1.已知集合A={-1,1,2,4},B={-1,0,2},那么A∪B=.2.已知i为虚数单位,那么复数=.3.若同时抛掷两枚骰子,则向上的点数之差的绝对值为4的概率是.4.若函数f(x)=sin(ω>0)的最小正周期为,则f=.5.某地政府调查了工薪阶层1000人的月工资收入,并根据调查结果绘制了如图所示的频率分布直方图.为了了解工薪阶层对月工资收入的满意程度,要采用分层抽样的方法从调查的1000人中抽出100人做电话询访,则(3000,3500]月工资收入段应抽出人.(第5题)6.执行如图所示的流程图,那么输出的M的值为.(第6题)7.已知曲线y=lnx的一条切线过原点,那么此切线的斜率为.8.在△ABC中,=2,若=m+n,则的值为.9.已知实数x,y满足约束条件且z=x+ay的最小值为7,则实数a=.10.已知数列{an}的首项为1,数列{bn}为等比数列,且bn=.若b10·b11=2,则a21=.11.在平面直角坐标系中,已知动圆C:(x-a)2+(y+2a-1)2=2(-1≤a≤1),直线l:y=x+b(b∈R).若动圆C总在直线l的下方,且它们至多有1个交点,则实数b的最小值是.12.若log4(3a+4b)=log2,则a+b的最小值是.13.已知函数f(x)=若f(f(a))≤2,则实数a的取值范围是.14.已知椭圆C:+=1(a>b>0)的离心率为e,直线l:y=ex+a与x轴、y轴分别交于点A,B,M是直线l与椭圆C的一个公共点.若AM=e·AB,则该椭圆的离心率e=.题号1234567答案题号891011121314答案二、解答题(本大题共4小题,共58分,解答时应写出必要的文字说明、证明过程或演算步骤)15.(本小题满分14分)在△ABC中,角A,B,C的对边分别是a,b,c,向量m=(5a-4c,4b)与n=(cosB,-cosC)垂直.(1)求cosB的值;...