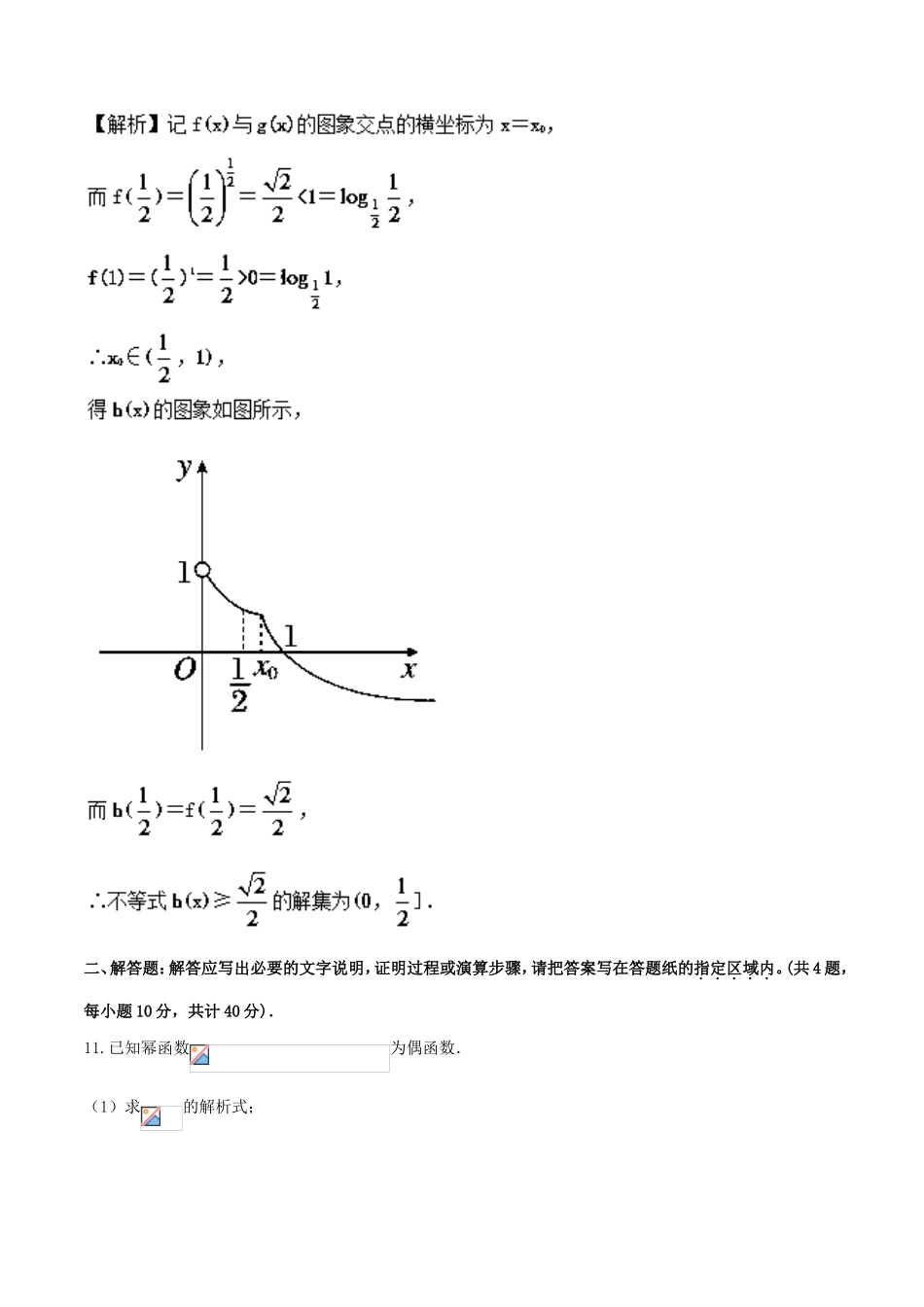
专题2.7对数与对数函数班级__________姓名_____________学号___________得分__________(满分100分,测试时间50分钟)一、填空题:请把答案直接填写在答题卡相应的位置上(共10题,每小题6分,共计60分).1.函数f(x)=log(x2-4)的单调递增区间为________.【答案】(-∞,-2)【解析】因为y=logt在定义域上是减函数,所以求原函数的单调递增区间,即求函数t=x2-4的单调递减区间,结合函数的定义域,可知所求区间为(-∞,-2).2.已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=3x+m(m为常数),则f(-log35)=________.【答案】-4【解析】因为函数f(x)是定义在R上的奇函数,所以f(0)=0,即30+m=0,解得m=-1,所以f(log35)=3log35-1=4,所以f(-log35)=-f(log35)=-4.3.计算log23log34+()log34=______.【答案】4【解析】log23log34+()log34=·+3log34=2+3log32=2+2=4.4.已知函数f(x)=lg,若f(a)=,则f(-a)=________.【答案】-5.函数f(x)=+lg的定义域为__________.【答案】(2,3)∪(3,4]【解析】由得故函数定义域为(2,3)∪(3,4].6.计算:lg0.001+ln+2-1+log23=________.【答案】-1【解析】原式=lg10-3+lne+2log2=-3++=-1.7.已知函数f(x)=关于x的方程f(x)+x-a=0有且只有一个实根,则实数a的取值范围是______.【答案】(1,+∞)【解析】问题等价于函数y=f(x)与y=-x+a的图象有且只有一个交点,结合函数图象可知a>1.8.函数f(x)=log2·log(2x)的最小值为______.【答案】-9.已知函数f(x)=alog2x-blog3x+2,若f=4,则f(2014)的值为________.【答案】0【解析】令g(x)=f(x)-2=alog2x-blog3x,可得g(x)满足g=-g(x).所以由g=f-2=2,得g(2014)=-2,所以f(2014)=0.10.已知函数,,记函数h(x)=,则不等式h(x)≥的解集为________.【答案】(0,]二、解答题:解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内。(共4题,每小题10分,共计40分).11.已知幂函数为偶函数.(1)求的解析式;(2)若函数在区间(2,3)上为单调函数,求实数的取值范围.【答案】(1);(2)或.【解析】(1)由为幂函数知,得或当时,,符合题意;当时,,不合题意,舍去.∴.(2)由(1)得,即函数的对称轴为,由题意知在(2,3)上为单调函数,所以或,即或.12.已知不等式的解集是}.(1)求a,b的值;(2)解不等式(c为常数).【答案】(1)(2)当时,当时,当时,13.已知函数f(x)是定义在R上的偶函数,f(0)=0,当x>0时,f(x)=logx.(1)求函数f(x)的解析式;(2)解不等式f(x2-1)>-2.解:(1)当x<0时,-x>0,则f(-x)=log(-x).因为函数f(x)是偶函数,所以f(-x)=f(x).所以函数f(x)的解析式为f(x)=14.设f(x)=loga(1+x)+loga(3-x)(a>0,a≠1),且f(1)=2.(1)求a的值及f(x)的定义域;(2)求f(x)在区间上的最大值.解:(1)因为f(1)=2,所以loga4=2(a>0,a≠1),所以a=2.由得x∈(-1,3),所以函数f(x)的定义域为(-1,3).(2)f(x)=log2(1+x)+log2(3-x)=log2(1+x)(3-x)=log2[-(x-1)2+4],所以当x∈(-1,1]时,f(x)是增函数;当x∈(1,3)时,f(x)是减函数,故函数f(x)在上的最大值是