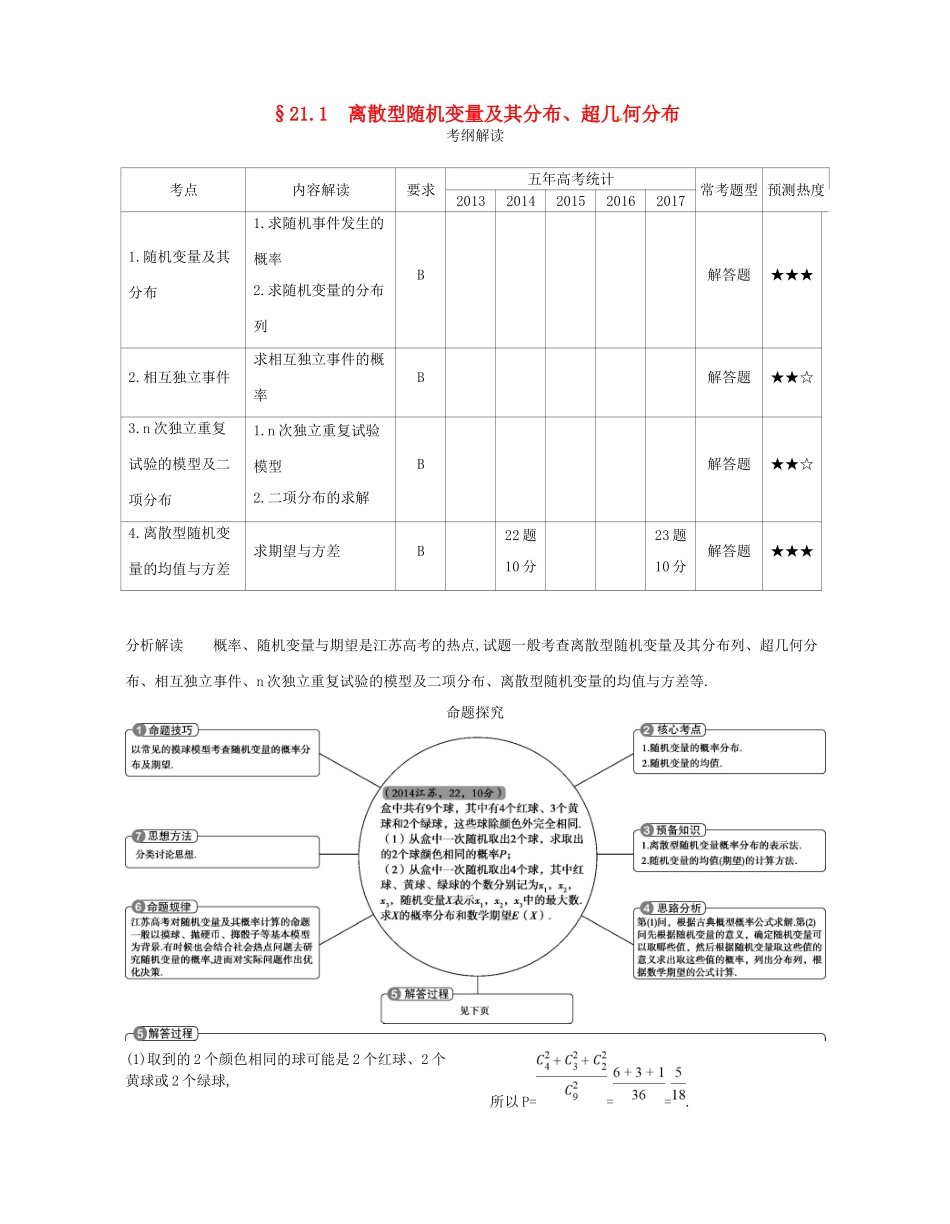
§21.1离散型随机变量及其分布、超几何分布考纲解读考点内容解读要求五年高考统计常考题型预测热度201320142015201620171.随机变量及其分布1.求随机事件发生的概率2.求随机变量的分布列B解答题★★★2.相互独立事件求相互独立事件的概率B解答题★★☆3.n次独立重复试验的模型及二项分布1.n次独立重复试验模型2.二项分布的求解B解答题★★☆4.离散型随机变量的均值与方差求期望与方差B22题10分23题10分解答题★★★分析解读概率、随机变量与期望是江苏高考的热点,试题一般考查离散型随机变量及其分布列、超几何分布、相互独立事件、n次独立重复试验的模型及二项分布、离散型随机变量的均值与方差等.命题探究(1)取到的2个颜色相同的球可能是2个红球、2个黄球或2个绿球,所以P===.(2)随机变量X所有可能的取值为2,3,4.{X=4}表示的随机事件是“取到的4个球是4个红球”,故P(X=4)==;{X=3}表示的随机事件是“取到的4个球是3个红球和1个其他颜色的球或3个黄球和1个其他颜色的球”,故P(X=3)===;于是P(X=2)=1-P(X=3)-P(X=4)=1--=.所以随机变量X的概率分布如下表:X234P因此随机变量X的数学期望E(X)=2×+3×+4×=.五年高考考点随机变量及其分布1.(2013广东理改编,4,5分)已知离散型随机变量X的分布列为X123P则X的数学期望E(X)=.答案2.(2017课标全国Ⅲ理,18,12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:最高气温[10,15)[15,20)[20,25)[25,30)[30,35)[35,40)天数216362574以最高气温位于各区间的频率代替最高气温位于该区间的概率.(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?解析本题考查随机变量的分布列,数学期望.(1)由题意知,X所有可能取值为200,300,500,由表格数据知P(X=200)==0.2,P(X=300)==0.4,P(X=500)==0.4.因此X的分布列为X200300500P0.20.40.4(2)由题意知,这种酸奶一天的需求量至多为500瓶,至少为200瓶,因此只需考虑200≤n≤500.当300≤n≤500时,若最高气温不低于25,则Y=6n-4n=2n;若最高气温位于区间[20,25),则Y=6×300+2(n-300)-4n=1200-2n;若最高气温低于20,则Y=6×200+2(n-200)-4n=800-2n.因此EY=2n×0.4+(1200-2n)×0.4+(800-2n)×0.2=640-0.4n.当200≤n<300时,若最高气温不低于20,则Y=6n-4n=2n;若最高气温低于20,则Y=6×200+2(n-200)-4n=800-2n.因此EY=2n×(0.4+0.4)+(800-2n)×0.2=160+1.2n.所以n=300时,Y的数学期望达到最大值,最大值为520元.3.(2017山东理,18,12分)在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用.现有6名男志愿者A1,A2,A3,A4,A5,A6和4名女志愿者B1,B2,B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.(1)求接受甲种心理暗示的志愿者中包含A1但不包含B1的概率;(2)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX.解析本题考查离散型随机变量的分布列,期望.(1)记接受甲种心理暗示的志愿者中包含A1但不包含B1的事件为M,则P(M)==.(2)由题意知X可取的值为0,1,2,3,4,则P(X=0)==,P(X=1)==,P(X=2)==,P(X=3)==,P(X=4)==.因此X的分布列为X01234PX的数学期望是EX=0×P(X=0)+1×P(X=1)+2×P(X=2)+3×P(X=3)+4×P(X=4)=0+1×+2×+3×+4×=2.4.(2016山东理,19,12分)甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语.在一轮活动中,如果两人都猜对,则“星队”得3分;如果只有一人猜对,则“星队”得1分;如果两人都没猜对,则“星队”得0分.已知甲每轮猜对的概率...