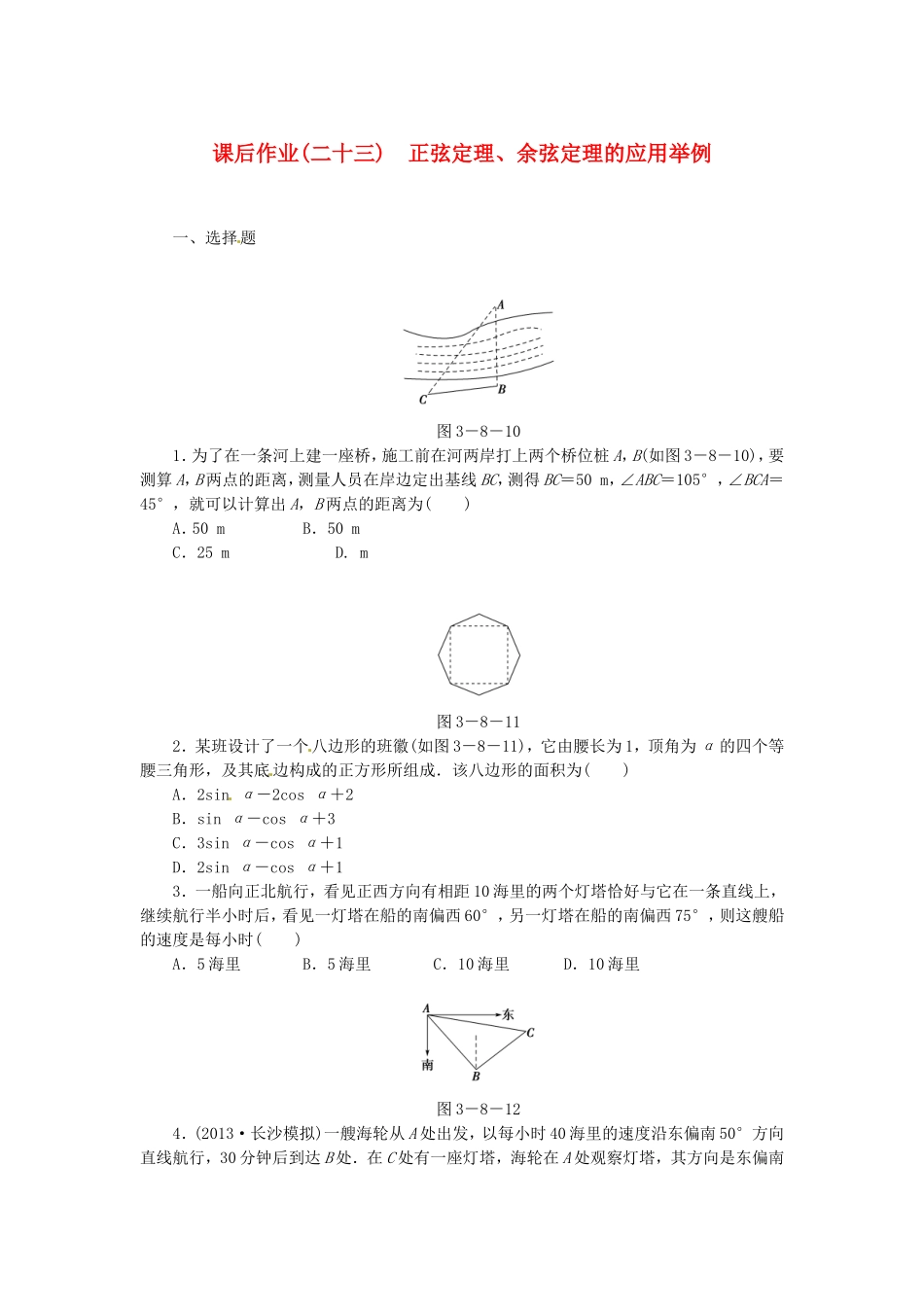
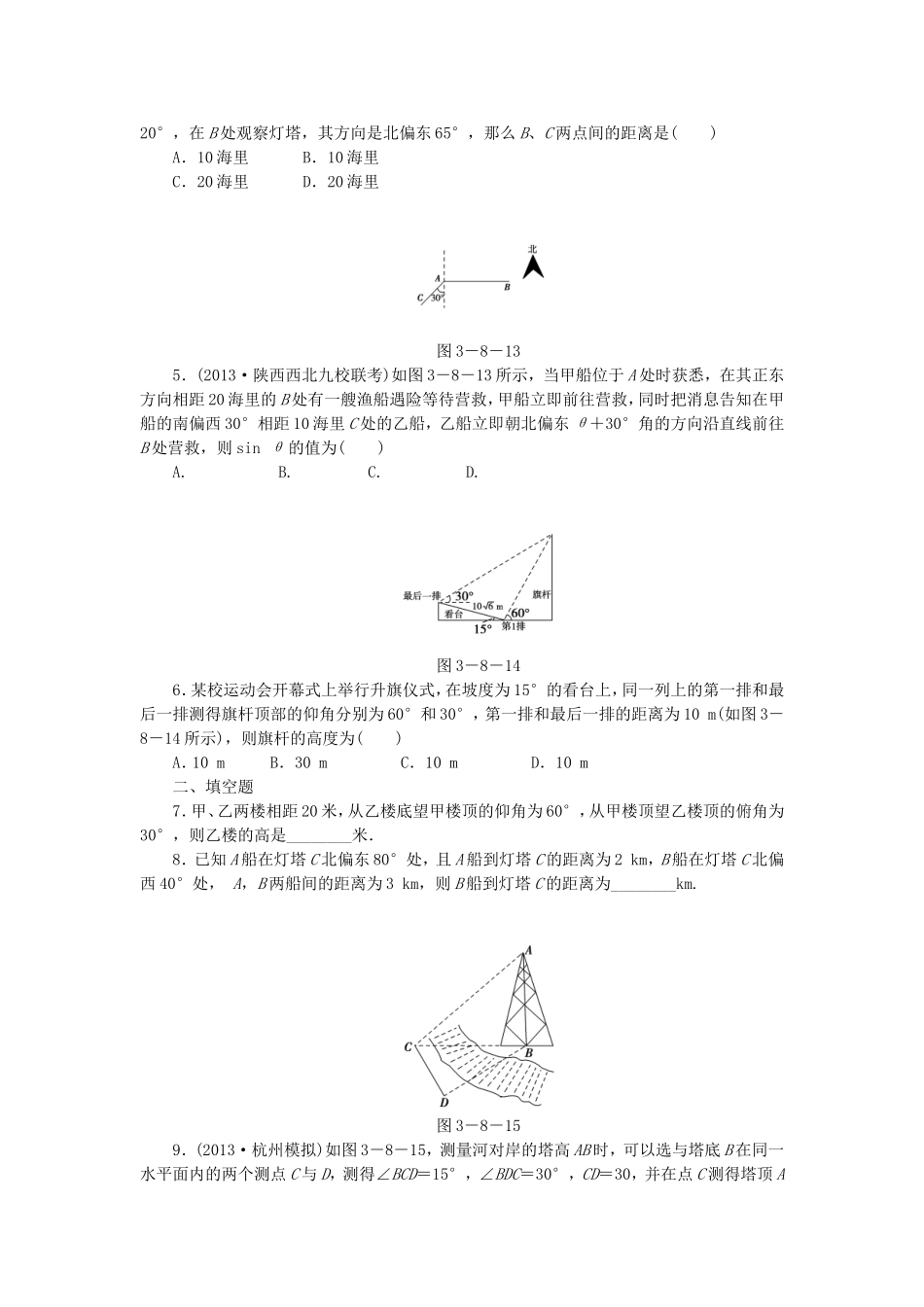
课后作业(二十三)正弦定理、余弦定理的应用举例一、选择题图3-8-101.为了在一条河上建一座桥,施工前在河两岸打上两个桥位桩A,B(如图3-8-10),要测算A,B两点的距离,测量人员在岸边定出基线BC,测得BC=50m,∠ABC=105°,∠BCA=45°,就可以计算出A,B两点的距离为()A.50mB.50mC.25mD.m图3-8-112.某班设计了一个八边形的班徽(如图3-8-11),它由腰长为1,顶角为α的四个等腰三角形,及其底边构成的正方形所组成.该八边形的面积为()A.2sinα-2cosα+2B.sinα-cosα+3C.3sinα-cosα+1D.2sinα-cosα+13.一船向正北航行,看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°,另一灯塔在船的南偏西75°,则这艘船的速度是每小时()A.5海里B.5海里C.10海里D.10海里图3-8-124.(2013·长沙模拟)一艘海轮从A处出发,以每小时40海里的速度沿东偏南50°方向直线航行,30分钟后到达B处.在C处有一座灯塔,海轮在A处观察灯塔,其方向是东偏南20°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是()A.10海里B.10海里C.20海里D.20海里图3-8-135.(2013·陕西西北九校联考)如图3-8-13所示,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救,甲船立即前往营救,同时把消息告知在甲船的南偏西30°相距10海里C处的乙船,乙船立即朝北偏东θ+30°角的方向沿直线前往B处营救,则sinθ的值为()A.B.C.D.图3-8-146.某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为10m(如图3-8-14所示),则旗杆的高度为()A.10mB.30mC.10mD.10m二、填空题7.甲、乙两楼相距20米,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则乙楼的高是________米.8.已知A船在灯塔C北偏东80°处,且A船到灯塔C的距离为2km,B船在灯塔C北偏西40°处,A,B两船间的距离为3km,则B船到灯塔C的距离为________km.图3-8-159.(2013·杭州模拟)如图3-8-15,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30,并在点C测得塔顶A的仰角为60°,则塔高AB=________.三、解答题图3-8-1610.(2013·济南模拟)如图3-8-16,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,这时此车距离A城多少千米?图3-8-1711.如图3-8-17,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=0.1km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D间的距离(计算结果精确到0.01km,≈1.414,≈2.449).图3-8-1812.(2013·石家庄模拟)某城市有一块不规则的绿地如图3-8-18所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为△ABC、△ABD,经测量AD=BD=14,BC=10,AC=16,∠C=∠D.(1)求AB的长度;(2)若建造环境标志的费用与用地面积成正比,不考虑其他因素,小李、小王谁的设计使建设费用最低,请说明理由.解析及答案一、选择题1.【解析】在△ABC中,由正弦定理=,AB=50.【答案】A2.【解析】三角形的底边长为x==,∴S=4S△+S正方形=4××1×1×sinα+x2=2sinα+2-2cosα=2sinα-2cosα+2.【答案】A3.【解析】如图,依题意有∠BAC=60°,∠BAD=75°,所以∠CAD=∠CDA=15°,从而CD=CA=10,在直角三角形ABC中,得AB=5,于是这艘船的速度是=10(海里/小时).【答案】C4.【解析】由已知可得,∠BAC=30°,∠ABC=105°,AB=20,从而∠ACB=45°.在△ABC中,由正弦定理,得BC=×sin30°=10.【答案】A5.【解析】连接BC.在△ABC中,AC=10,AB=20,∠BAC=120°...