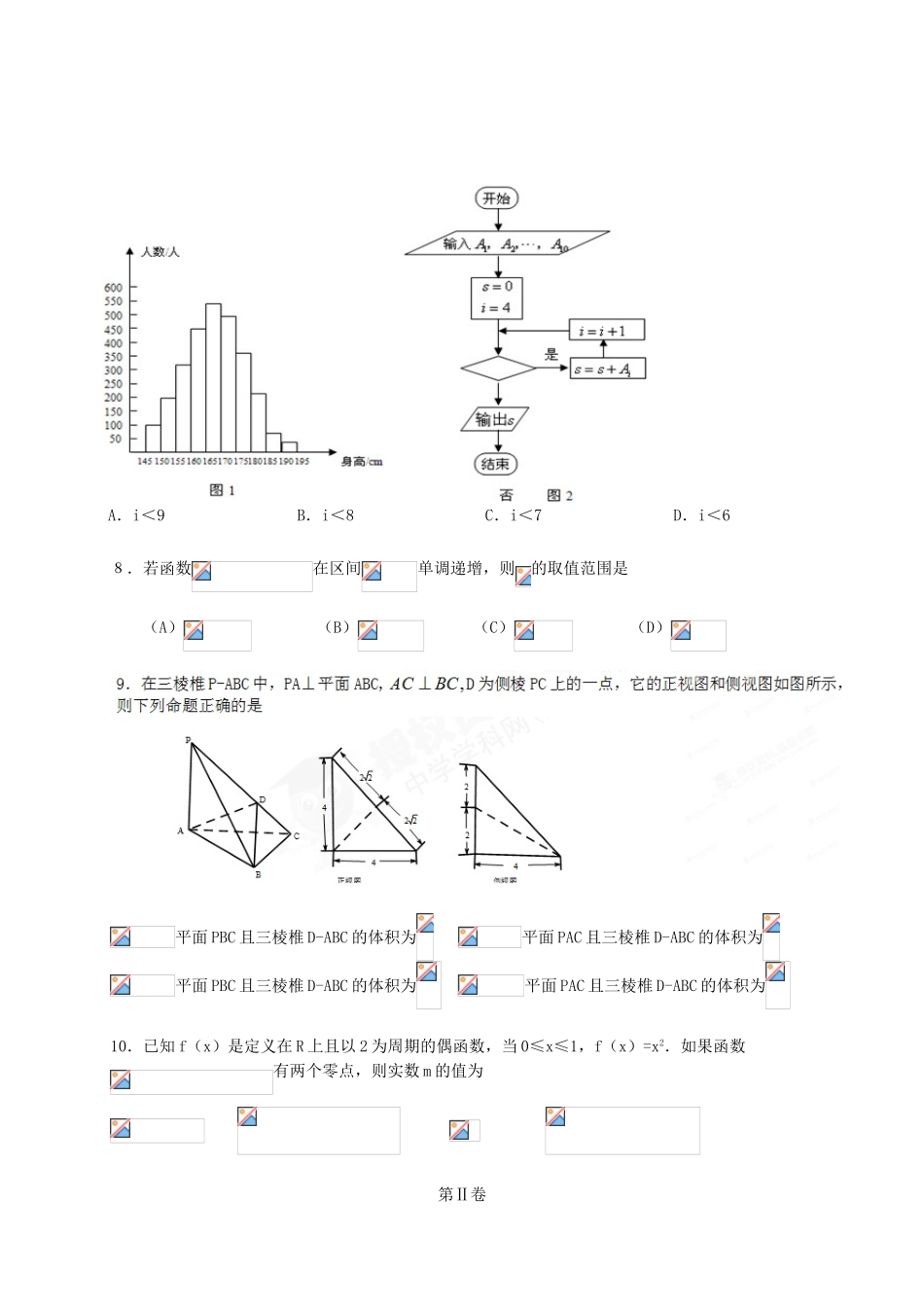
第二次月考数学理试题【四川版】本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷一、选择题:本大题共10小题,每小题5分,共50分.1.若复数(为虚数单位)为实数,则实数A.0B.-1C.-1或1D.12.已知全集U=R,集合则3.将函数的图像沿轴向左平移个单位后,得到一个偶函数的图像,则的最小值为4.设是非零向量,已知命题P:若,,则;命题q:若,则,则下列命题中真命题是()A.B.C.D.5.将包含甲、乙两队的8支队伍平均分成2个小组参加某项比赛,则甲、乙两队被分在不同小组的分组方案有A.种B.种C.种D.种6.函数的图像大致是A.B.C.D.7.如图1是某县参加年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为A1,A2,…,A10(如A2表示身高(单位:cm)在[150,155)内的学生人数).图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~185cm(含160cm,不含185cm)的学生人数,那么在流程图中的判断框内应填写的条件是()A.i<9B.i<8C.i<7D.i<68.若函数在区间单调递增,则的取值范围是(A)(B)(C)(D)平面PBC且三棱椎D-ABC的体积为平面PAC且三棱椎D-ABC的体积为平面PBC且三棱椎D-ABC的体积为平面PAC且三棱椎D-ABC的体积为10.已知f(x)是定义在R上且以2为周期的偶函数,当0≤x≤1,f(x)=x2.如果函数有两个零点,则实数m的值为第Ⅱ卷二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中横线上.11.(x-2)的展开式中的系数为.(用数字作答)12.已知函数,则的值为13.已知函数f(x)=3x+cos2x+sin2x,a=,则过曲线y=x3上一个点P(a,b)的切线方程为。14.设函数,若,则.15.定义“正对数”:现有四个命题:①若②若③若④若其中真命题有____________.(写出所有真命题的编号)三、解答题:本大题共6小题,满分75分.其中16-19每题12分,20题13分,21题14分.16.已知在锐角三角形中,分别为角A,B,C的对边,(1)求角C的值;(2)设函数,且两个相邻最高点之间的距离为,求f(A)的值域.17.已知等差数列的公差它的前项和为,若且成等比数列.(1)求数列的通项公式;(2)设数列的前项和为,求证:18.将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落,小球在整个下落过程中它将3次遇到黑色障碍物,最后落入A袋或B袋中。已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是。(1)求小球落入B袋中的概率P(B)(2)在容器入口处依次放入2个小球,记落入A袋中的小球个数为,试求的分布列和的数学期E。19.如图,在三棱柱中,是边长为2的等边三角形,平面,D,E,I分别是,的中点.(1)求证:平面;(2)若H为上的动点,与平面所成的最大角的正切值为,求侧棱的长.(3)在(2)的条件下,求二面角I-BD-A的余弦值.20.圆的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图).(Ⅰ)求点P的坐标;(Ⅱ)焦点在x轴上的椭圆C过点P,且与直线交于A,B两点,若的面积为2,求C的标准方程.xyOP21.设函数,,其中为实数.(1)若在上是单调减函数,且在上有最小值,求的取值范围;(2)若在上是单调增函数,试求的零点个数,并证明你的结论.参考答案9.解:又由三视图可得又故10.11.-16012.13.3x-y-2=0或3x-4y+1=014.15.①③④16.解:(1)(2),值域为[-,]解:(1)由题意得IGF解得(2)递增19.解:(1)法1:取中点证法二:延长交AC延长线于F证法三:证(2)又等边,E是中点所以,连接EH,则所以EH最短时最大此时,由平几相似关系得(3)20.(Ⅰ)设切点坐标为.则切线斜率为.切线方程为.即.此时,两个坐标轴的正半轴于切线围成的三角形面积.由知当且仅当时,有最大值.即有最小值.因此点的坐标为.(Ⅱ)设的标准方程为.点.由点在上知.并由得.又是方程的根,因此,由,,得.由点到直线的距离为及得.解得或.因此,(舍)或,.从而所求的方程为.21.解:(1)≤0在上恒成立,则≥,.故:≥1.,若1≤≤e,则≥0在上恒成立,此时,在上是单调增函数,无最小值,不合;若>e,则在上是...