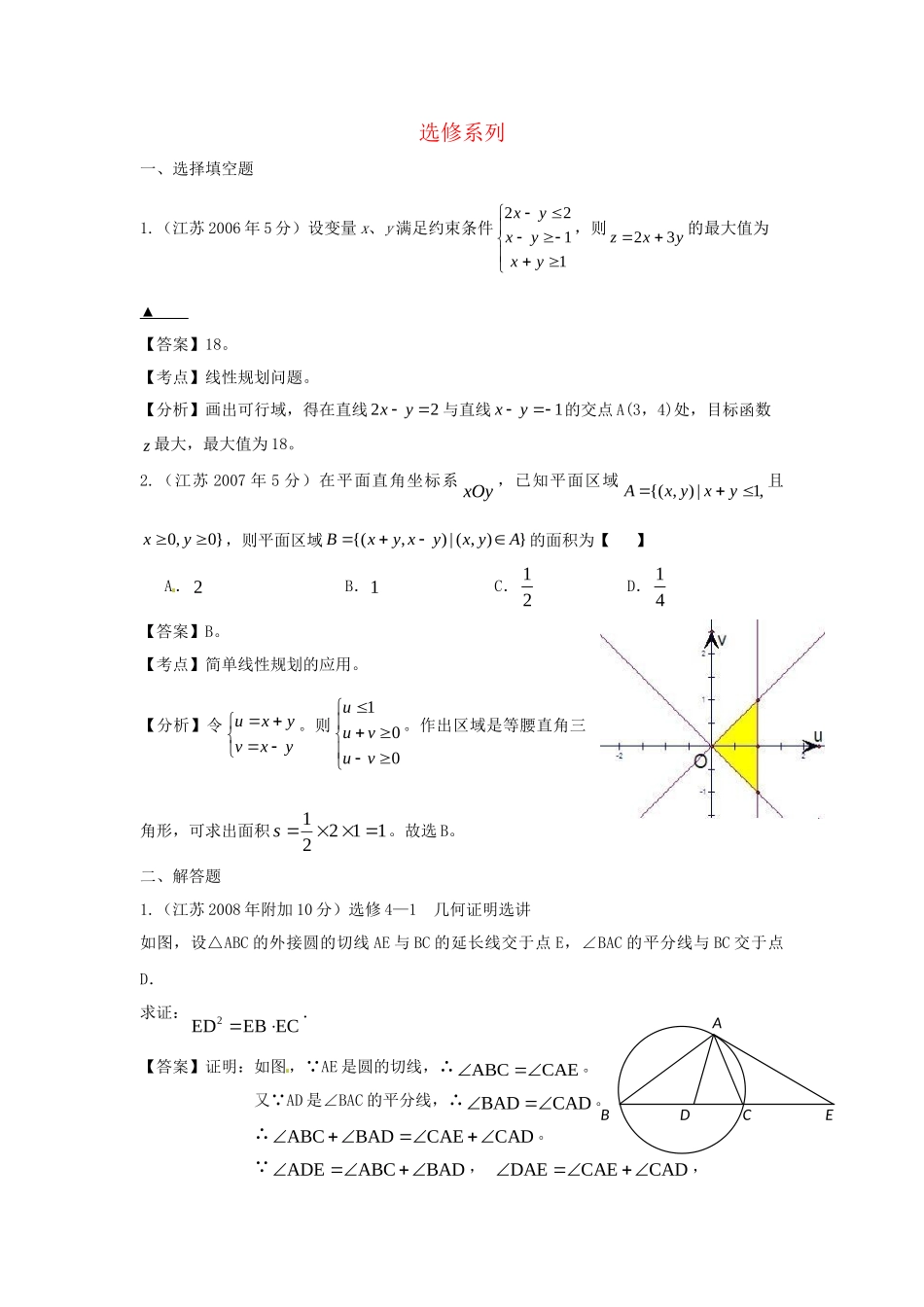
选修系列一、选择填空题1.(江苏2006年5分)设变量x、y满足约束条件1122yxyxyx,则yxz32的最大值为▲【答案】18。【考点】线性规划问题。【分析】画出可行域,得在直线22xy与直线1xy的交点A(3,4)处,目标函数z最大,最大值为18。2.(江苏2007年5分)在平面直角坐标系xOy,已知平面区域{(,)|1,Axyxy且0,0}xy,则平面区域{(,)|(,)}BxyxyxyA的面积为【】A.2B.1C.12D.14【答案】B。【考点】简单线性规划的应用。【分析】令uxyvxy。则100uuvuv。作出区域是等腰直角三角形,可求出面积11221s。故选B。二、解答题1.(江苏2008年附加10分)选修4—1几何证明选讲如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D.求证:2EDEBEC.【答案】证明:如图, AE是圆的切线,∴ABCCAE。又 AD是∠BAC的平分线,∴BADCAD。∴ABCBADCAECAD。 ADEABCBAD,DAECAECAD,BCEDA∴ADEDAE。∴EA=ED。 EA是圆的切线,∴由切割线定理知,2EAECEB。而EA=ED,∴2EDEBEC。【考点】与圆有关的比例线段。【分析】根据已知EA是圆的切线,AC为过切点A的弦得两个角相等,再结合角平分线条件,从而得到△EAD是等腰三角形,再根据切割线定理即可证得。2.(江苏2008年附加10分)选修4—2矩阵与变换在平面直角坐标系xOy中,设椭圆2241xy在矩阵对应的变换作用下得到曲线F,求F的方程.【考点】圆的标准方程,矩阵变换的性质。【分析】由题意先设椭圆上任意一点00(,)Pxy,根据矩阵与变换的公式求出对应的点'''00(,)Pxy,得到两点的关系式,再由点P在椭圆上代入化简。3.(江苏2008年附加10分)选修4—4参数方程与极坐标在平面直角坐标系xOy中,点()Pxy,是椭圆2213xy上的一个动点,求Sxy的最大值.【答案】解: 椭圆2213xy的参数方程为3cos(sinxy为参数)∴可设动点P的坐标为(3cos,sin),其中02.∴313cossin2(cossin)2sin()223Sxy∴当6时,S取最大值2。【考点】椭圆的参数方程【分析】先根据椭圆的标准方程进行三角代换表示椭圆上任意一点,然后利用三角函数的辅助角公式进行化简,即可求出所求。4.(江苏2008年附加10分)选修4—5不等式证明选讲设a,b,c为正实数,求证:33311123abc+abc≥.【答案】证明: ,,abc为正实数,∴由平均不等式可得33333331111113abcabc,即3331113abcabc。∴3331113abcabcabcabc。又 33223abcabcabcabc,∴33311123abc+abc≥。【考点】平均值不等式,不等式的证明。【分析】先根据平均值不等式证明3331113abcabcabcabc,再证323abcabc。5.(江苏2009年附加10分)选修4-1:几何证明选讲如图,在四边形ABCD中,△ABC≌△BAD.求证:AB∥CD.【答案】证明: △ABC≌△BAD,∴∠ACB=∠BDA。∴A、B、C、D四点共圆,∴∠CBA=∠CDB。又 △ABC≌△BAD,∴∠CAB=∠DBA。∴∠DBA=∠CDB。∴AB∥CD。【考点】全等三角形的性质,四点共圆的判定,圆周角定理,平行的判定。【分析】由△ABC≌△BAD得∠ACB=∠BDA,故A、B、C、D四点共圆,从而∠CBA=∠CDB。再由△ABC≌△BAD得∠CAB=∠DBA。因此∠DBA=∠CDB,所以AB∥CD。6.(江苏2009年附加10分)选修4-2:矩阵与变换求矩阵3221A的逆矩阵.【答案】解:设矩阵A的逆矩阵为,xyzw则3210,2101xyzw即323210,2201xzywxzyw∴3212032021xzxzywyw。解得:1,2,2,3xzyw。∴A的逆矩阵为112A23。【考点】逆矩阵的求法。【分析】设出逆矩阵,根据逆矩阵的定义计算即可。7.(江苏2009年附加10分)选修4-4:坐标系与参数方程已知曲线C的参数方程为113()xttytt(t为参数,0t).求曲线C的普通方程。【答案】解: 212,xtt...