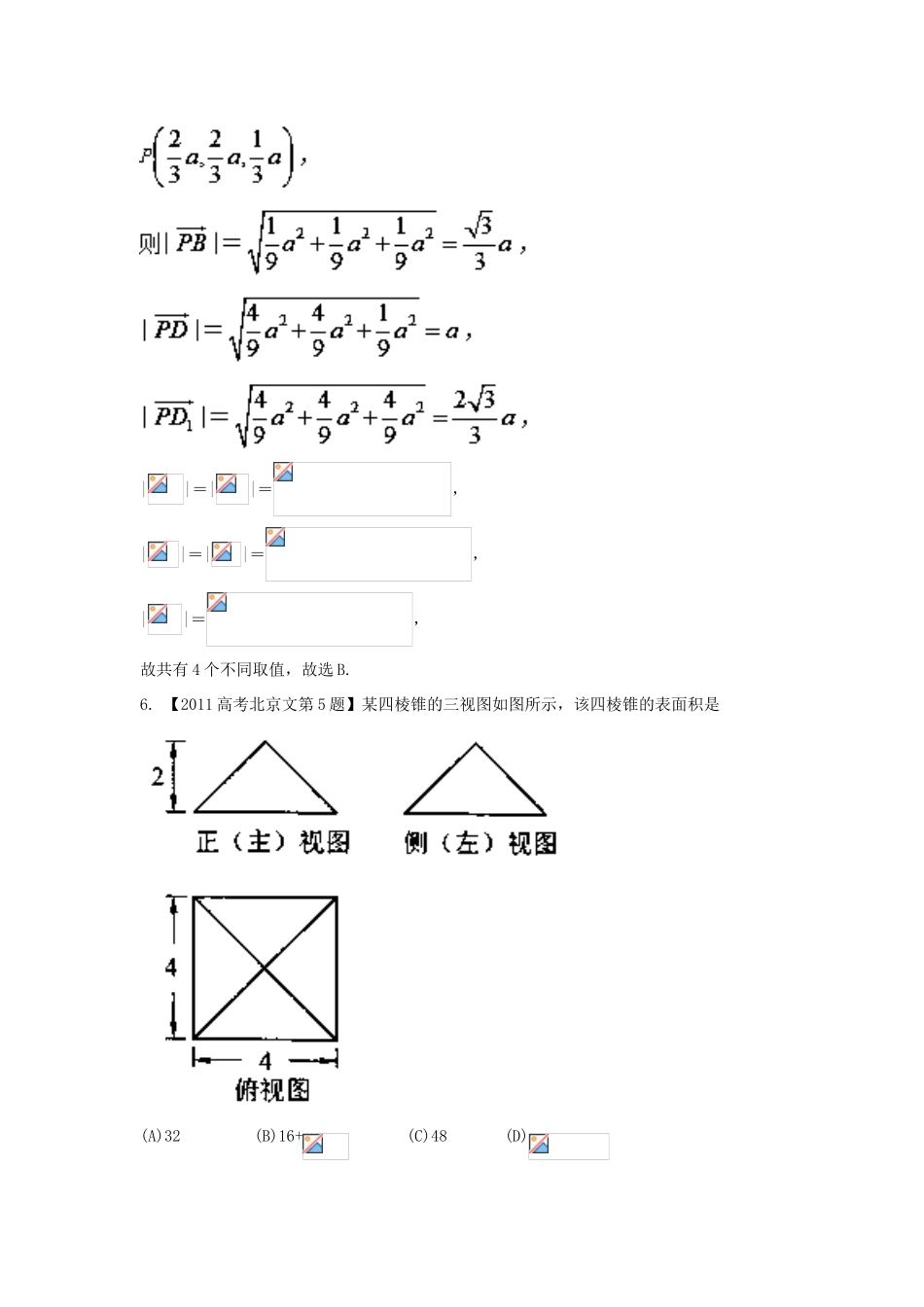
专题10立体几何1.【2009高考北京文第7题】若正四棱柱的底面边长为1,与底面ABCD成60°角,则到底面ABCD的距离为()A.B.1C.D.【答案】D2.【2010高考北京文第5题】一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如图所示,则该几何体的俯视图为()【答案】C【解析】试题分析:由几何体的正视图、侧视图,并结合题意可知,选C项.3.【2010高考北京文第8题】如图,正方体ABCD—A1B1C1D1的棱长为2,动点E,F在棱A1B1上,点Q是棱CD的中点,动点P在棱AD上.若EF=1,DP=x,A1E=y(x,y大于零),则三棱锥P—EFQ的体积()A.与x,y都有关B.与x,y都无关C.与x有关,与y无关D.与y有关,与x无关【答案】C4.【2012高考北京文第7题】某三棱锥的三视图如图所示,该三棱锥的表面积是()A.B.C.D.【答案】B【解析】试题分析:根据三棱锥的三视图可还原此几何体的直观图为此几何体为一个底面为直角三角形,高为4的三棱锥,因此表面积为S=×(2+3)×4+×4×5+×4×(2+3)+.5.【2013高考北京文第8题】如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,P到各顶点的距离的不同取值有().A.3个B.4个C.5个D.6个【答案】B【解析】试题分析:设正方体的棱长为a.建立空间直角坐标系,如图所示.则D(0,0,0),D1(0,0,a),C1(0,a,a),C(0,a,0),B(a,a,0),B1(a,a,a),A(a,0,0),A1(a,0,a),||=||=,||=||=,||=,故共有4个不同取值,故选B.6.【2011高考北京文第5题】某四棱锥的三视图如图所示,该四棱锥的表面积是(A)32(B)16+(C)48(D)【答案】B【解析】由三视图可知,几何体为底面边长为4,高为2的正四棱锥,则四棱锥的斜高为,表面积,故选B.7.【2006高考北京文第7题】设A、B、C、D是空间四个不同的点.在下列命题中,不正确的是()A.若AC与BD共面,则AD与BC共面B.若AC与BD是异面直线,则AD与BC是异面直线C.若AB=AC,DB=DC,则AD=BCD.若AB=AC,DB=DC,则AD⊥BC【答案】C故AD与BC是异面直线.选项D,如图所示,取BC中点M,由AB=AC,DB=DC,得AM⊥BC,DM⊥BC.又AM∩DM=M,∴BC⊥面AMD.∴BC⊥AD.选项C,无法推断.8.【2007高考北京文第7题】平面平面的一个充分条件是()A.存在一条直线B.存在一条直线C.存在两条平行直线D.存在两条异面直线【答案】D【考点】线线平行于线面平行的判定定理和性质,异面直线的概念,充分条件的判断9.【2005高考北京文第7题】在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的是()(A)BC//平面PDF(B)DF⊥平面PAE(C)平面PDF⊥平面ABC(D)平面PAE⊥平面ABC【答案】C【解析】由DF∥BC可得BC∥平面PDF,故A正确.若PO⊥平面ABC,垂足为O,则O在AE上,则DF⊥PO,又DF⊥AE,故DF⊥平面PAE,故B正确.由DF⊥平面PAE可得,平面PAE⊥平面ABC,故D正确.故选C.10.【2017高考北京文数第6题】某三棱锥的三视图如图所示,则该三棱锥的体积为(A)60(B)30(C)20(D)10【答案】D【考点】三视图,几何体的体积【名师点睛】本题考查了空间想象能力,由三视图还原几何体的方法:如果我们死记硬背,不会具体问题具体分析,就会选错,实际上,这个题的俯视图不是几何体的底面,因为顶点在底面的射影落在了底面三角形的外面,否则中间的那条线就不会是虚线.11.【2015高考北京,文7】某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为()A.B.C.D.【答案】C【解析】四棱锥的直观图如图所示:【考点定位】三视图.12.【2013高考北京文第10题】某四棱锥的三视图如图所示,该四棱锥的体积为__________.【答案】3【解析】13.【2016高考北京文数】某四棱柱的三视图如图所示,则该四棱柱的体积为___________.【答案】【解析】试题分析:四棱柱高为1,底面为等腰梯形,面积为,因此体积为考点:三视图【名师点睛】解决此类问题的关键是根据几何体的三视图判断几何体的结构特征.常见的有以下几类:①三视图为三个三角形,对应的几何体为三棱锥;②三视图为两个三角形,一个四边形,对应的几何体为四棱锥;③三视图为两个三角形,一个圆,对应的几何体为圆锥;④三视图为一个三角形,两个四边形...