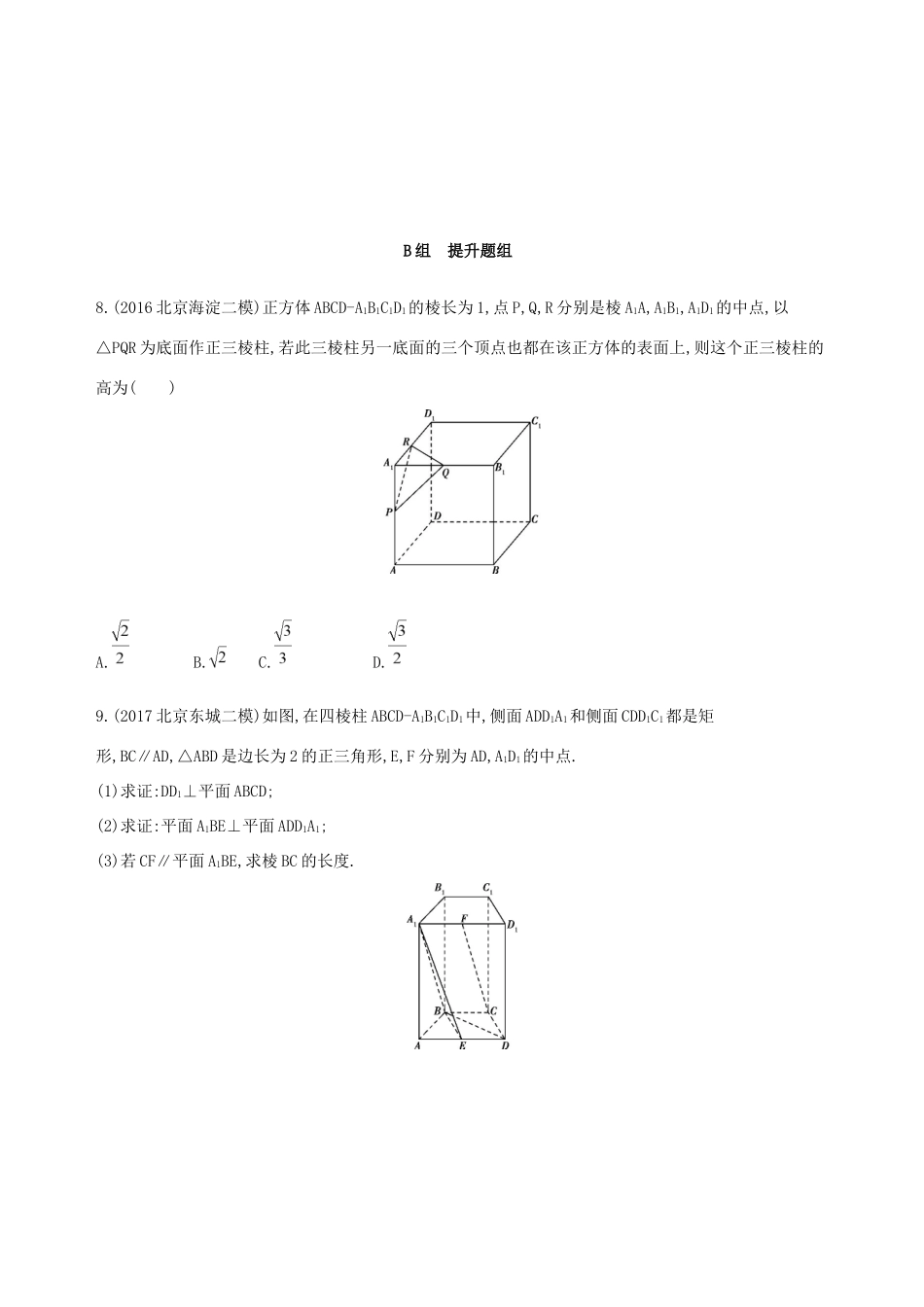
第五节直线、平面垂直的判定与性质A组基础题组1.已知在空间四边形ABCD中,AD⊥BC,AD⊥BD,且△BCD是锐角三角形,则必有()A.平面ABD⊥平面ADCB.平面ABD⊥平面ABCC.平面ADC⊥平面BDCD.平面ABC⊥平面BDC2.如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.将△ADB沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列结论正确的是()A.平面ABD⊥平面ABCB.平面ADC⊥平面BDCC.平面ABC⊥平面BDCD.平面ADC⊥平面ABC3.(2017北京朝阳期中)设m,n是两条不同的直线,α,β是两个不同的平面.下列命题正确的是()A.若m⊂α,n⊂β,m⊥n,则α⊥βB.若α∥β,m⊥α,n∥β,则m⊥nC.若α⊥β,m⊥α,n∥β,则m∥nD.若α⊥β,α∩β=m,n⊥m,则n⊥β4.(2015北京西城二模)在长方体ABCD-A1B1C1D1中,AB=,BC=AA1=1,点P为对角线AC1上的动点,点Q为底面ABCD上的动点(点P、Q可以重合),则B1P+PQ的最小值为()A.B.C.D.25.(2017北京,18,14分)如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.(1)求证:PA⊥BD;(2)求证:平面BDE⊥平面PAC;(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.6.(2017北京朝阳期中)如图,四边形ABCD为矩形,PA⊥平面ABCD,DE∥PA.(1)求证:BC⊥CE;(2)若直线m⊂平面PAB,试判断直线m与平面CDE的位置关系,并说明理由;(3)若AB=PA=2DE=2,AD=3,求三棱锥E-PCD的体积.7.(2018北京朝阳期中)如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥平面ABCD,E是棱PA上的一个动点.(1)若E为PA的中点,求证:PC∥平面BDE;(2)求证:平面PAC⊥平面BDE;(3)若三棱锥P-BDE的体积是四棱锥P-ABCD的体积的,求的值.B组提升题组8.(2016北京海淀二模)正方体ABCD-A1B1C1D1的棱长为1,点P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作正三棱柱,若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个正三棱柱的高为()A.B.C.D.9.(2017北京东城二模)如图,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1和侧面CDD1C1都是矩形,BC∥AD,△ABD是边长为2的正三角形,E,F分别为AD,A1D1的中点.(1)求证:DD1⊥平面ABCD;(2)求证:平面A1BE⊥平面ADD1A1;(3)若CF∥平面A1BE,求棱BC的长度.10.(2018北京海淀期末)如图,三棱柱ABC-A1B1C1中,侧面ABB1A1⊥底面ABC,AC⊥AB,AC=AB=AA1=2,∠AA1B1=60°,E,F分别为棱A1B1,BC的中点.(1)求证:AC⊥AE;(2)求三棱柱ABC-A1B1C1的体积;(3)在直线AA1上是否存在一点P,使得CP∥平面AEF.若存在,求出AP的长;若不存在,请说明理由.11.(2016北京西城二模)如图,在周长为8的矩形ABCD中,E,F分别为BC,DA的中点.将矩形ABCD沿着线段EF折起,使得∠DFA=60°.设G为AF上一点,且满足CF∥平面BDG.(1)求证:EF⊥DG;(2)求证:G为线段AF的中点;(3)求线段CG长度的最小值.答案精解精析A组基础题组1.C AD⊥BC,AD⊥BD,BC∩BD=B,∴AD⊥平面BDC,又AD⊂平面ADC,∴平面ADC⊥平面BDC.2.D易证BD⊥CD.因为平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,CD⊂平面BCD,故CD⊥平面ABD,则CD⊥AB.又AD⊥AB,AD∩CD=D,AD⊂平面ADC,CD⊂平面ADC,故AB⊥平面ADC.又AB⊂平面ABC,∴平面ADC⊥平面ABC.3.B由m,n是两条不同的直线,α,β是两个不同的平面知:在A中,若m⊂α,n⊂β,m⊥n,则α与β相交或平行,故A错误;在B中,若α∥β,m⊥α,n∥β,则m⊥β,m⊥n,故B正确;在C中,若α⊥β,m⊥α,n∥β,则m与n相交、平行或异面,故C错误;在D中,若α⊥β,α∩β=m,n⊥m,则n与β相交、平行或n⊂β,故D错误.故选B.4.C5.解析本题考查线面垂直的判定和性质,面面垂直的判定及线面平行的性质,三棱锥的体积.考查空间想象能力.(1)因为PA⊥AB,PA⊥BC,所以PA⊥平面ABC.又因为BD⊂平面ABC,所以PA⊥BD.(2)因为AB=BC,D为AC中点,所以BD⊥AC.由(1)知,PA⊥BD,所以BD⊥平面PAC.因为BD⊂平面BDE,所以平面BDE⊥平面PAC.(3)因为PA∥平面BDE,平面PAC∩平面BDE=DE,所以PA∥DE.因为D为AC的中点,所以DE=PA=1,BD=DC=.由(1)知,PA⊥平面ABC,所以DE⊥平面ABC.所以三棱锥E-BCD的体积V=BD·DC·DE=.6.解析(1)证明:因为PA⊥底面ABCD,PA∥DE,所以DE⊥底面ABCD.所以DE⊥BC.因为四边形ABCD为矩形,所以BC⊥CD.又因为CD∩DE=D,所以BC⊥平面CDE,所以BC⊥CE.(2)直线m∥平面CDE.证明如下:因为...