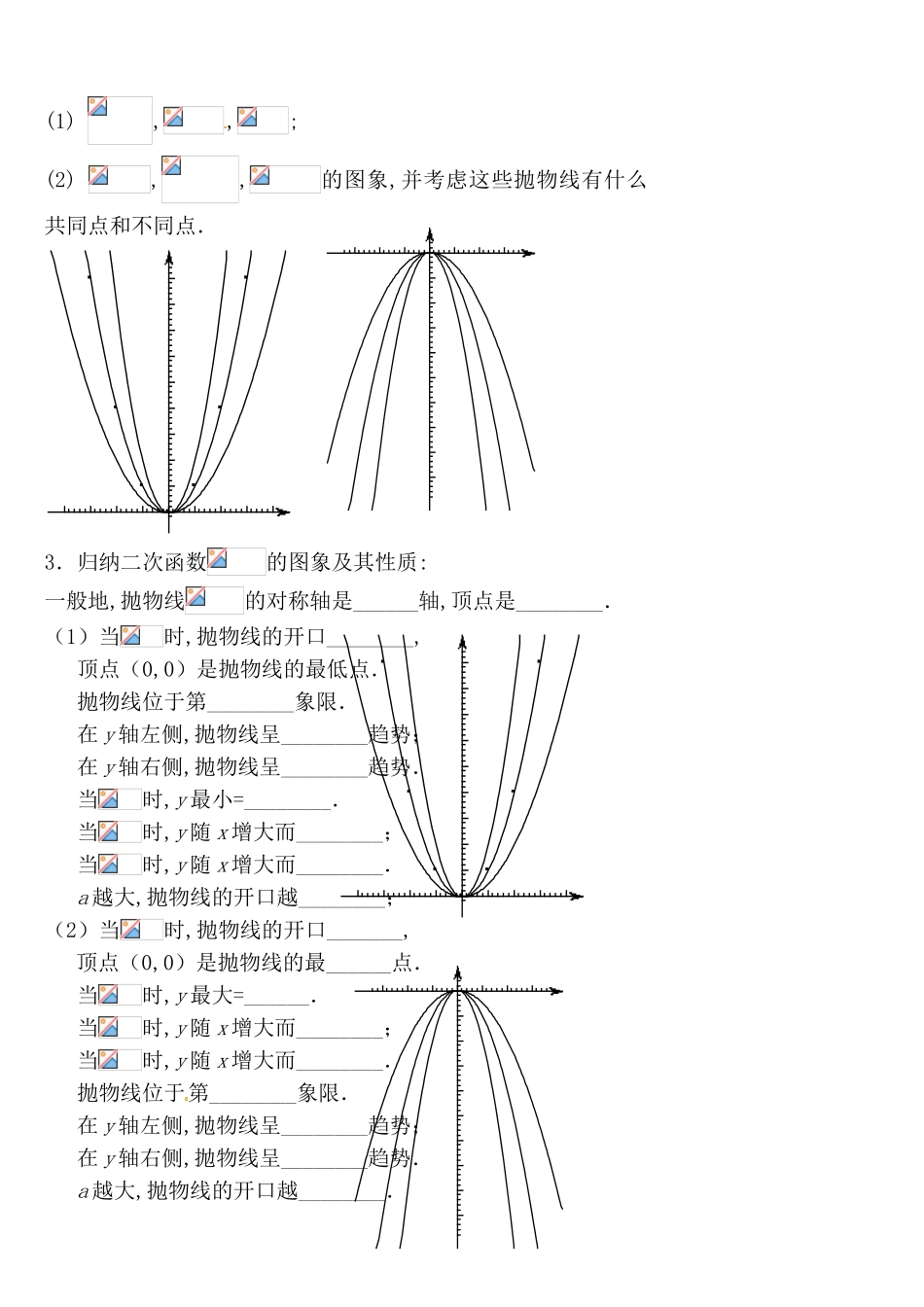
二次函数y=ax(a≠0)与y=ax+c(a≠0)的图象与性质一、最简单的二次函数1.画出二次函数的图象——画图步骤?如何列表?解:在中,自变量x为任意实数.列表如下:描点,用平滑曲线顺次连接各点.1.画出二次函数的图象:2.归纳二次函数的图象性质:形状、大小和位置.(1)这条曲线叫做抛物线.一般地,二次函数的图象叫做抛物线.(2)开口方向:_________.(3)对称轴:____________________;对称轴方程:.思考如何进行证明?(,y)和(-x,y)都在同一条抛物线上.(4)顶点:抛物线与其对称轴的交点(0,0),即原点.顶点是抛物线的最_____点;即当时,y取________值.(5)图象位于第________象限.形:在y轴左侧,抛物线呈________趋势;在y轴右侧,抛物线呈________趋势.数:当时,y随x的增大而________;当时,y随x的增大而________.探究:分别在同一平面直角坐标系中,画出下列两组函数:(1),,;(2),,的图象,并考虑这些抛物线有什么共同点和不同点.3.归纳二次函数的图象及其性质:一般地,抛物线的对称轴是______轴,顶点是________.(1)当时,抛物线的开口________,顶点(0,0)是抛物线的最低点.抛物线位于第________象限.在y轴左侧,抛物线呈________趋势;在y轴右侧,抛物线呈________趋势.当时,y最小=________.当时,y随x增大而________;当时,y随x增大而________.a越大,抛物线的开口越________;(2)当时,抛物线的开口_______,顶点(0,0)是抛物线的最______点.当时,y最大=______.当时,y随x增大而________;当时,y随x增大而________.抛物线位于第________象限.在y轴左侧,抛物线呈________趋势;在y轴右侧,抛物线呈________趋势.a越大,抛物线的开口越________.(3)大,抛物线的开口越________;越小,抛物线的开口越________.二、二次函数的图象和性质在同一平面直角坐标系中,画出,的图象.解:列表利用平移变换,描点画图,得到和的图象.把抛物线向上平移1个单位,就得到抛物线;把抛物线向下平移1个单位,就得到抛物线.1.二次函数的图象是抛物线,其性质是:(1)当时,开口方向、对称轴、增减性与相同,不同的是顶点坐标为(____,____),当时,y最小=________.(2)当时,开口方向、对称轴、增减性与相同,不同的是顶点坐标为(____,____),当时,y最大=________.2.抛物线与有何联系?(1)抛物线与的形状完全_______,只是在坐标系中的_______不同.(2)抛物线向_______平移_______个单位长度得到抛物线;抛物线向_______平移______个单位长度得到抛物线;练习:1.(1)二次函数与的形状相同,开口大小一样,开口方向相反,则.(2)不计算比较大小:函数的图象左侧上有两点A(a,15),B(b,0.5),则ab.2.(1)抛物线的开口方向,对称轴是,顶点坐标是.(2)抛物线与的形状相同,其顶点坐标为(0,1),则其解析式为.(3)抛物线向平移个单位后,得到抛物线3.在同一平面直角坐标系中,一次函数与二次函数的图象大致为().A.B.C.D.