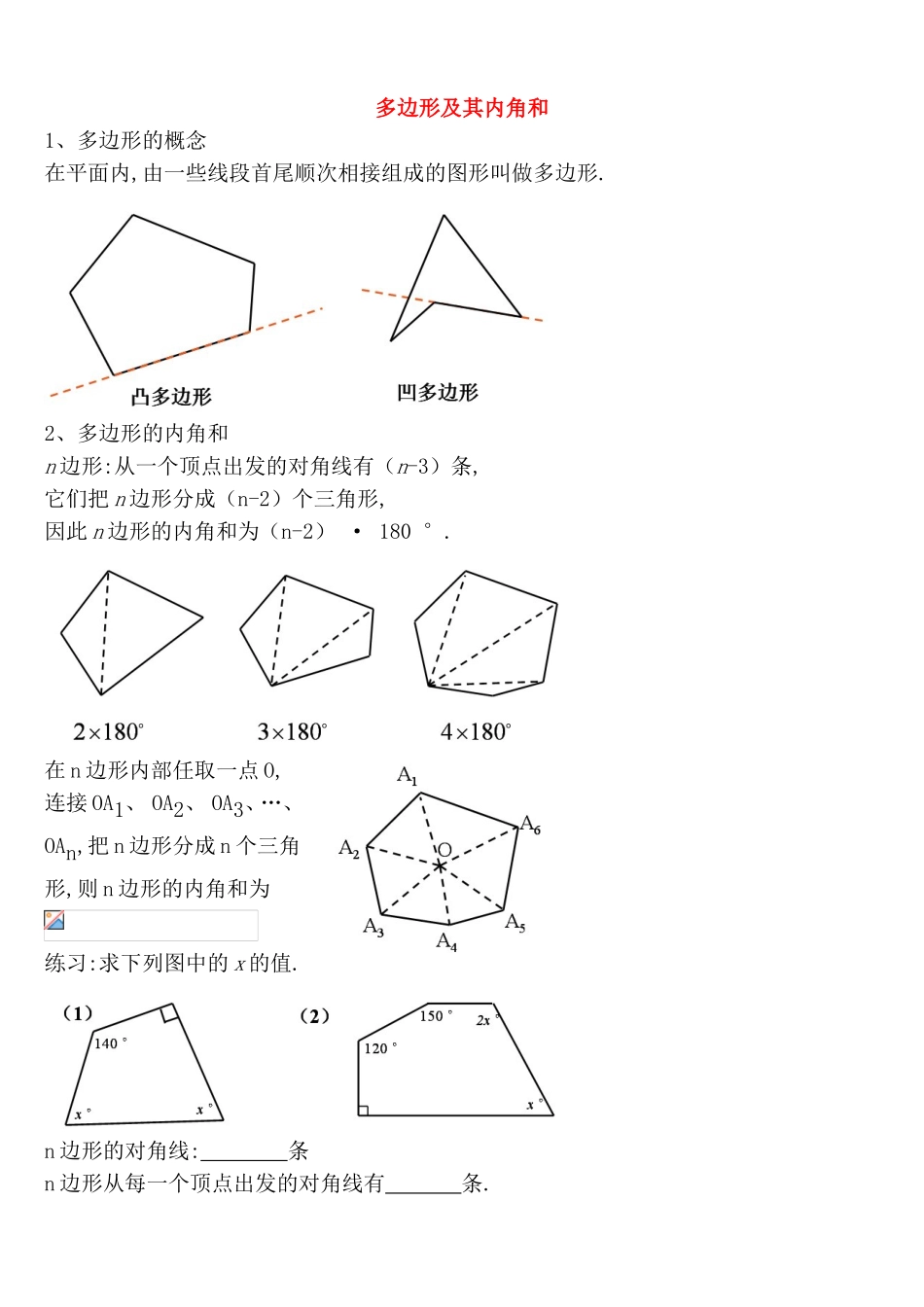
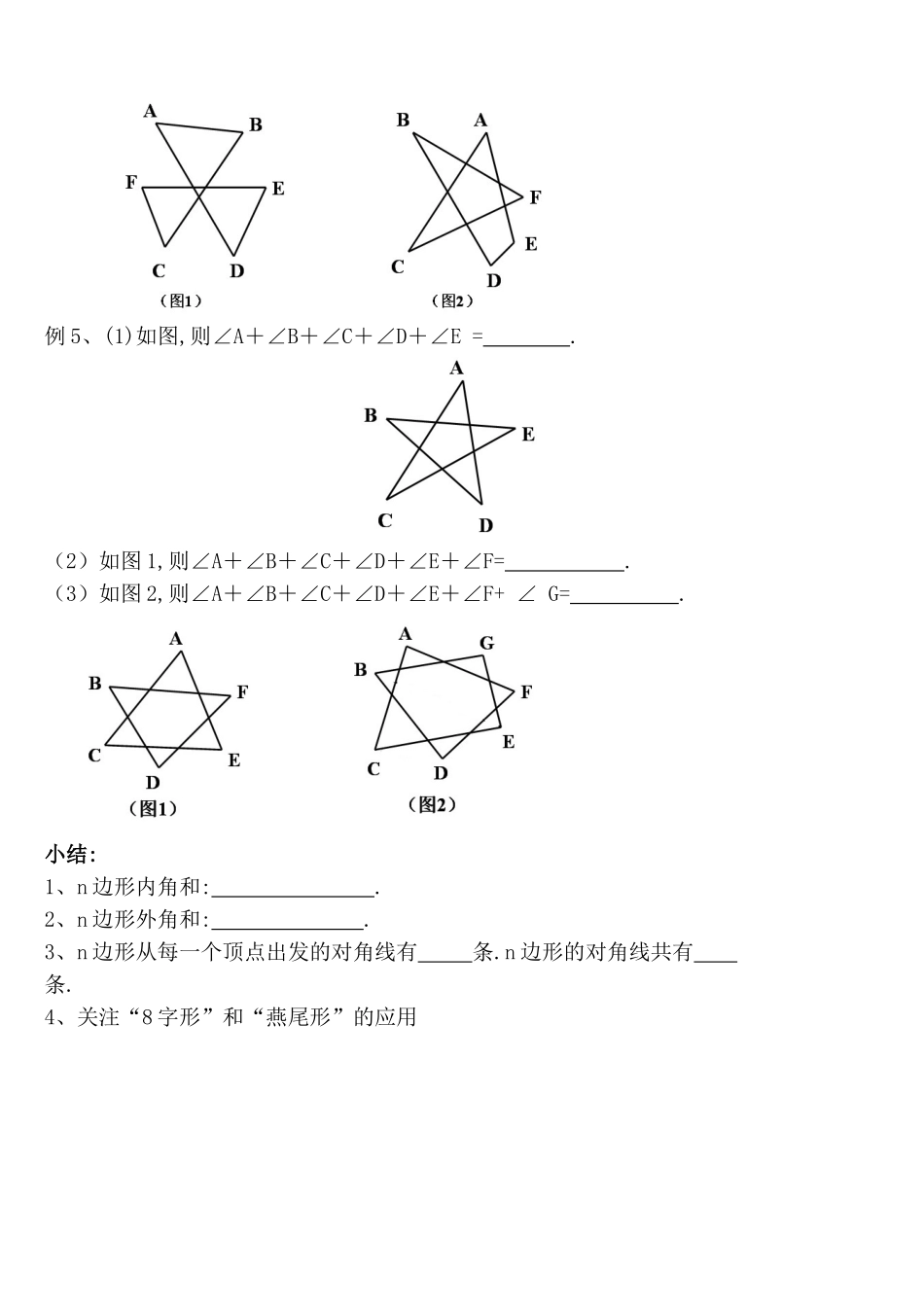
多边形及其内角和1、多边形的概念在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.2、多边形的内角和n边形:从一个顶点出发的对角线有(n-3)条,它们把n边形分成(n-2)个三角形,因此n边形的内角和为(n-2)·180°.在n边形内部任取一点O,连接OA1、OA2、OA3、…、OAn,把n边形分成n个三角形,则n边形的内角和为练习:求下列图中的x的值.n边形的对角线:条n边形从每一个顶点出发的对角线有条.3、多边形的外角和分析:(1)任何一个外角与它相邻的内角有什么关系?(2)五边形的5个外角加上与它们相邻的内角,所得总和是多少?(3)上述总和与五边形的内角和、外角和有什么关系?结论:五边形的外角和为n边形的内角和、外角和有什么关系?结论:n边形的外角和为如何理解:从多边形的一个顶点A出发,沿多边形的各边走过各顶点,再回到点A,然后转向出发时的方向.在行程中所转的各个角的和,就是多边形的外角和,由于走了一周,因此所转的各个角的和等于一个周角.例1、(1)一个多边形的内角和是540º,那么这个多边形的对角线的条数是.(2)已知一个多边形的内角和与外角和共2160º,则这个多边形的边数是.例2、(1)一个凸多边形的内角和与它的一个外角的和为2005º,求多边形的边数。(2)如果一个凸多边形,除了一个内角以外,其它内角的和为2570°,求这个没有计算在内的内角的度数.例3、若多边形最多有四个钝角,那么此多边形的边数最多是______.例4、(1)如图1,则∠A+∠B+∠C+∠D+∠E+∠F=.(2)如图2,则∠A+∠B+∠C+∠D+∠E+∠F=.例5、(1)如图,则∠A+∠B+∠C+∠D+∠E=.(2)如图1,则∠A+∠B+∠C+∠D+∠E+∠F=.(3)如图2,则∠A+∠B+∠C+∠D+∠E+∠F+∠G=.小结:1、n边形内角和:.2、n边形外角和:.3、n边形从每一个顶点出发的对角线有条.n边形的对角线共有条.4、关注“8字形”和“燕尾形”的应用