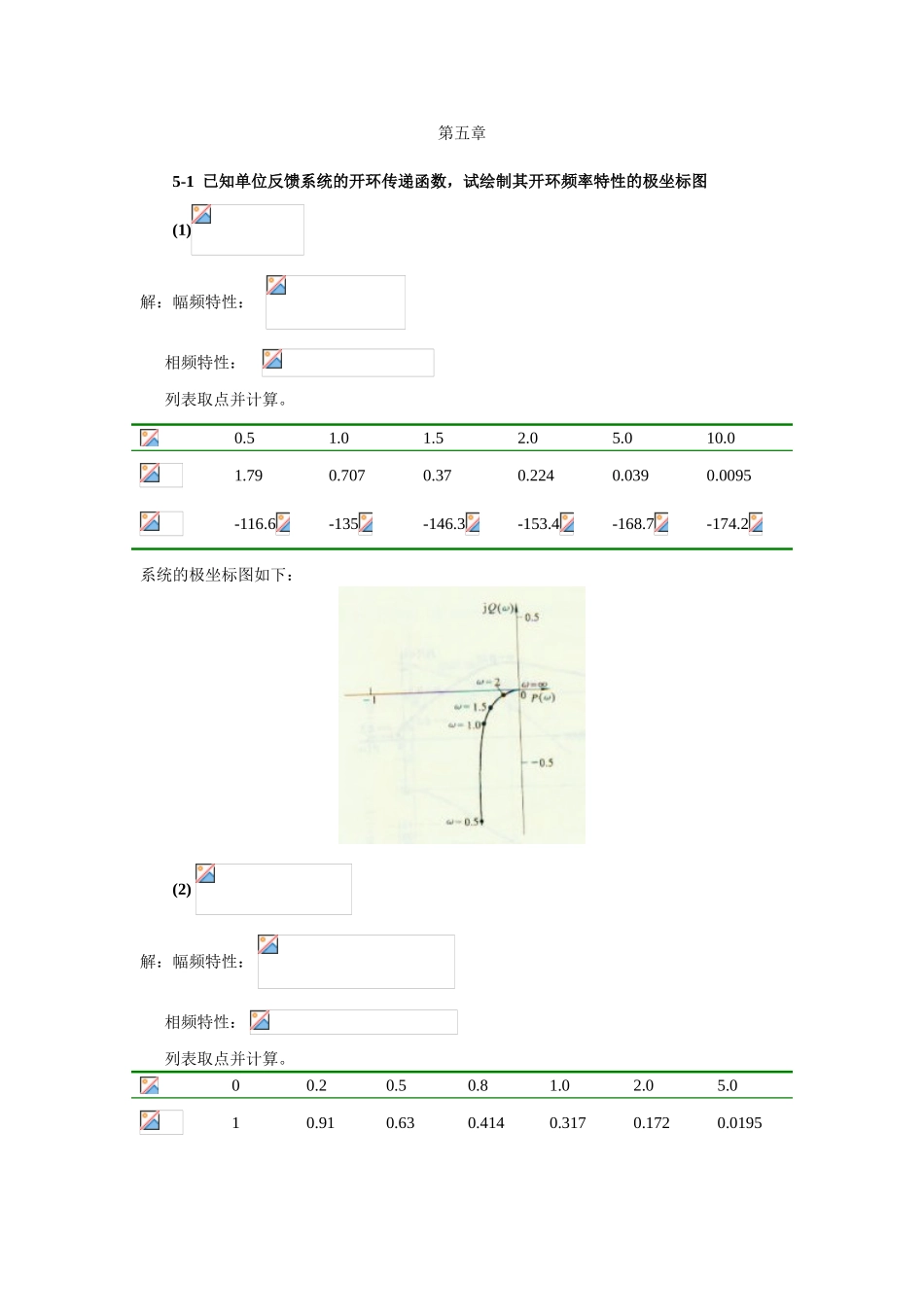
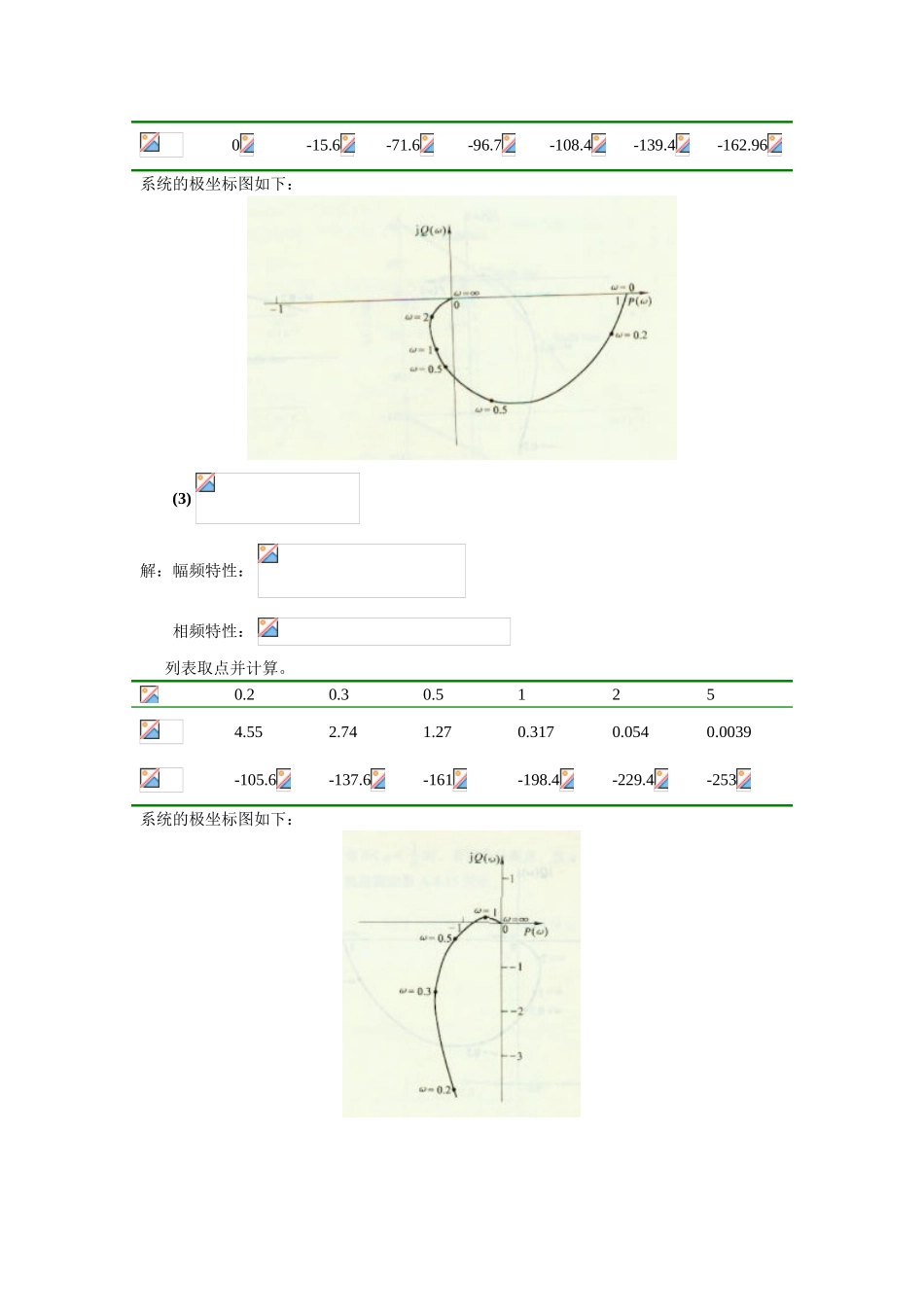
第五章5-1已知单位反馈系统的开环传递函数,试绘制其开环频率特性的极坐标图(1)解:幅频特性:相频特性:列表取点并计算。0.51.01.52.05.010.01.790.7070.370.2240.0390.0095-116.6-135-146.3-153.4-168.7-174.2系统的极坐标图如下:(2)解:幅频特性:相频特性:列表取点并计算。00.20.50.81.02.05.010.910.630.4140.3170.1720.01950-15.6-71.6-96.7-108.4-139.4-162.96系统的极坐标图如下:(3)解:幅频特性:相频特性:列表取点并计算。0.20.30.51254.552.741.270.3170.0540.0039-105.6-137.6-161-198.4-229.4-253系统的极坐标图如下:(4)解:幅频特性:相频特性:列表取点并计算。0.20.250.30.50.60.8122.7513.87.862.520.530.650.317-195.6-220.6-227.6-251.6-261.6-276.7-288.4系统的极坐标图如下:5-2试绘制上题中各系统的开环对数频率特性(伯德图)。(1)解:系统为Ⅰ型,伯德图起始斜率为-20dB/dec,在处与=20=0相交。环节的交接频率,斜率下降20dB/dec,变为-40dB/dec。系统的伯德图如图所示:(2)解:伯德图起始为0dB线,的交接频率,斜率下降20dB/dec,变为-20dB/dec。的交接频率,斜率下降20dB/dec,变为-40dB/dec。系统的伯德图如图所示。(3)解:系统为Ⅰ型,伯德图起始斜率为-20dB/dec,其延长线在=1处与=20=0相交。的交接频率,斜率下降20dB/dec,变为-40dB/dec。的交接频率,斜率下降20dB/dec,变为-60dB/dec。系统的伯德图如图所示。(4)解:系统为错误!未找到引用源。型,伯德图起始斜率为-40dB/dec,其延长线在=1处与=20=0相交;的交接频率,斜率下降20dB/dec,变为-60dB/dec。的交接频率,斜率下降20dB/dec,变为-80dB/dec。系统的伯德图如图所示。5-3设单位反馈系统的开环传递函数为试绘制系统的内奎斯特图和伯德图,并求相角裕度和增益裕度。解:幅频特性:相频特性0.51.01.52.03.05.010.017.38.95.33.51.770.670.24-106.89-122.3-135.4-146.3-163-184.76-213.7错误!未找到引用源。系统的极坐标图如图所示。令,解得。,增益裕度:GM=dB。错误!未找到引用源。伯德图起始斜率为-20dB/dec,经过点。处斜率下降为-40dB/dec,处斜率下将为-60dB/dec。系统的伯德图如下图所示。令=1得剪切频率,相角裕度PM=3.94deg。5-5已知单位反馈系统的开环传递函数为用MATLAB绘制系统的伯德图,确定的频率,和对应的相角。解:命令如下:>>s=tf('s');>>G=1/((s*(1+s)^2));>>margin(G2);程序执行结果如上,可从图中直接读出所求值。5-6根据下列开环频率特性,用MATLAB绘制系统的伯德图,并用奈氏稳定判据判断系统的稳定性。(1)解:命令如下:>>s=tf('s');>>G=10/(s*(0.1*s+1)*(0.2*s+1));>>margin(G);如图,相角裕度和增益裕度都为正,系统稳定。(2)解:命令如下:>>s=tf('s');>>G=2/((s^2)*(0.1*s+1)*(10*s+1));>>margin(G);如图,增益裕度无穷大,相角裕度-83,系统不稳定。5-7已知最小相位系统的开环对数幅频特性的渐近线如图所示,试写出系统的开环传递函数,并汇出对应的对数相频曲线的大致图形。(a)解:低频段由得,=2处,斜率下降20dB/dec,对应惯性环节。由上可得,传递函数。相频特性。汇出系统的相频特性曲线如下图所示。(b)解:低频段斜率为-20dB/dec,对应积分环节。=2处,斜率下降20dB/dec,对应惯性环节。在剪切频率处,,解得传递函数为:(c)低频段斜率为-40dB/dec,为两个积分环节的叠加;处,斜率上升20dB/dec,对应一阶微分环节;处,斜率下降20dB/dec,对应一阶惯性环节传递函数形式为:图中所示Bode图的低频段可用传递函数为来描述,则其幅频特性为。取对数,得。同理,Bode图中斜率为-20dB/dec的中频段可用来描述,则其对数幅频特性为。由图有,dB,则有。再看图,由可解得综上,系统开环传递函数为(参考李友善做法)系统相频特性:曲线如下:5-8设系统开环频率特性的极坐标图如图5-T-2所示,试判断闭环系统的稳定性。(a)解:系统开环稳定,奈氏图包围(-1,0j)点一次,P≠0,所以闭环系统不稳定。(b)解:正负穿越各一次,P=2(N+-N-)=0,闭环系统稳定。(c)闭环系统稳定。(d)闭环系统稳定。5-9根据系统的开环传递函数绘制系统的伯德图,并...