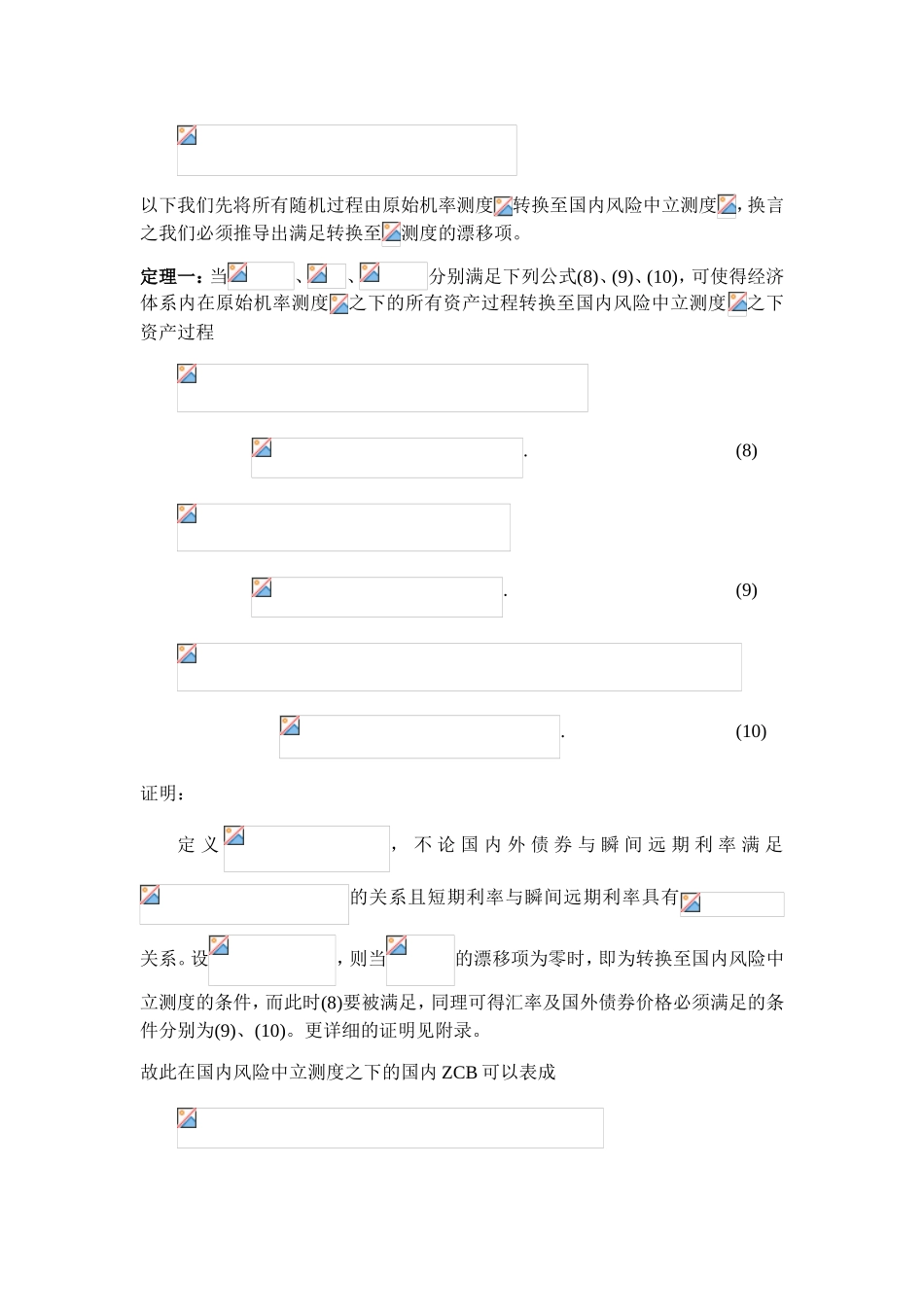
利率外汇价格服从扩散跳跃过程的零息债券数学模型假设存在一个于时段可连续交易的经济体,且经济体系中不确定性可以用机率空间来描述,其中为样本空间,为-algebra,为原始机率测度,令为所产生的filtration。相对应维度的Levy过程,描述如下:.(1)其中为空间下的测度函数,使得当时且当时为可积分,、为中向量,为一个对称且凖正定矩阵,使得且,代表Euclideanvectornorm而可为任一矩阵的norm。公式(1)是Levy过程所对应的特征函数,我们利用特征函数来表述Levy过程是因为特征函数与Levy过程是一对一关系,换言之定义的特征函数,相当于定义。而满足公式(1)的也可以用积分表之:(2)其中是维度的布朗运动,测度跳跃幅度,是受补偿函数,是的长度开根号。定义特征函数,而可表为特征函数的指数函数形式,如下:.(3)也就是透过公式(2)可得(4)根据Huang和Hung的论文得知,如果可以用适当的函数表示为,则可以改写为.(5)接着利用(2)所定义的Levy过程建构一个跨国经济体,右上标为d表示国内,右上标为f表示国外,符号定义如下:表现在时间为,时间瞬间借/贷的国内远期利率,到期日为时支付1元的国内零息债券(ZCB)时间时国内瞬间无风险利率,同理,国外的瞬间远期利率、瞬间短期利率、国外ZCB,分别为、、,假设在机率测度之下,国内外瞬间远期利率的动态行为遵循下列随机过程:,(6).(7)其中与皆为有界且在为一给定的数值;同时、及、前者为空间中被给定之函数,后者为空间中被给定之函数,而定义域为。根据国内外债券与瞬间远期利率满足的关系,在机率测度之下ZCB过程可表为,其中and,至于汇率过程假设为以下形式:以下我们先将所有随机过程由原始机率测度转换至国内风险中立测度,换言之我们必须推导出满足转换至测度的漂移项。定理一:当、、分别满足下列公式(8)、(9)、(10),可使得经济体系内在原始机率测度之下的所有资产过程转换至国内风险中立测度之下资产过程.(8).(9).(10)证明:定义,不论国内外债券与瞬间远期利率满足的关系且短期利率与瞬间远期利率具有关系。设,则当的漂移项为零时,即为转换至国内风险中立测度的条件,而此时(8)要被满足,同理可得汇率及国外债券价格必须满足的条件分别为(9)、(10)。更详细的证明见附录。故此在国内风险中立测度之下的国内ZCB可以表成在测度之下的汇率过程可表为在测度之下的国外ZCB表为(11)引理一:假设则相对应的短期利率过程为,其中表示对函数的第二个变量偏微分,也就是。证明:因为远期利率与债券价格具有关系,将(11)先取ln然后再取,又因为短期利率与远期利率满足,将T设为t代入即可得之证明。定理二:假设国内外远期利率过程皆符合HJM模型,并且假设,其中是严格递增函数,则时国外ZCB价格可以表为,其中(12)(13)证明:根据(11)可推论并且可将(11)写为(14)又令,并且计算,可得带回(14),可得设故可得证。附录A:假设及在国内风险中立测度之下,与的漂移项要为零且的漂移项要为。首先我们证明将从测度转换为测度,所必需满足的条件,根据本文的假设Levy过程可以表为(A1).(A1)将(A1)带入,可改写为.(A2)将(A2)及带入,可得.(A3)设,将(A3)以微分的方式表示如下.测度之下,当满足下式,则的漂移项为零.(A4)接着,求出将从转移至,其漂移项所必需满足的条件,假设且.(A5)将(A5)带入,可重新写成.(A6)设.则(A6)的微分形式可以表为下式.测度之下,当满足下式,则的漂移项为.(A7)最后求出将从转移至,其漂移项所必需满足的条件,假设.(A8)将(A8)带入,可得..测度之下,当满足下式,则的漂移项为零.(A9)将(A7)带入(A9),可得.(A10)