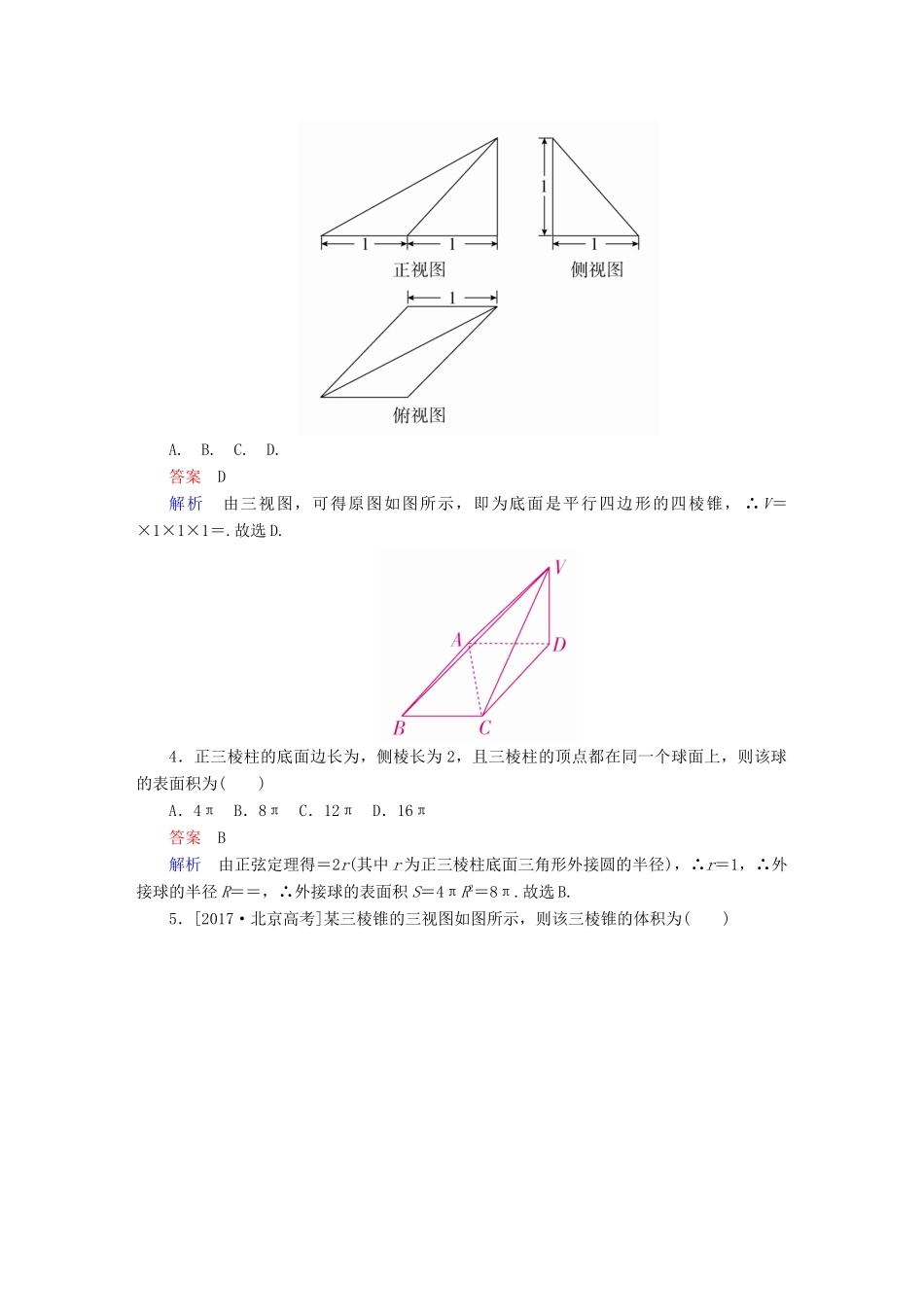
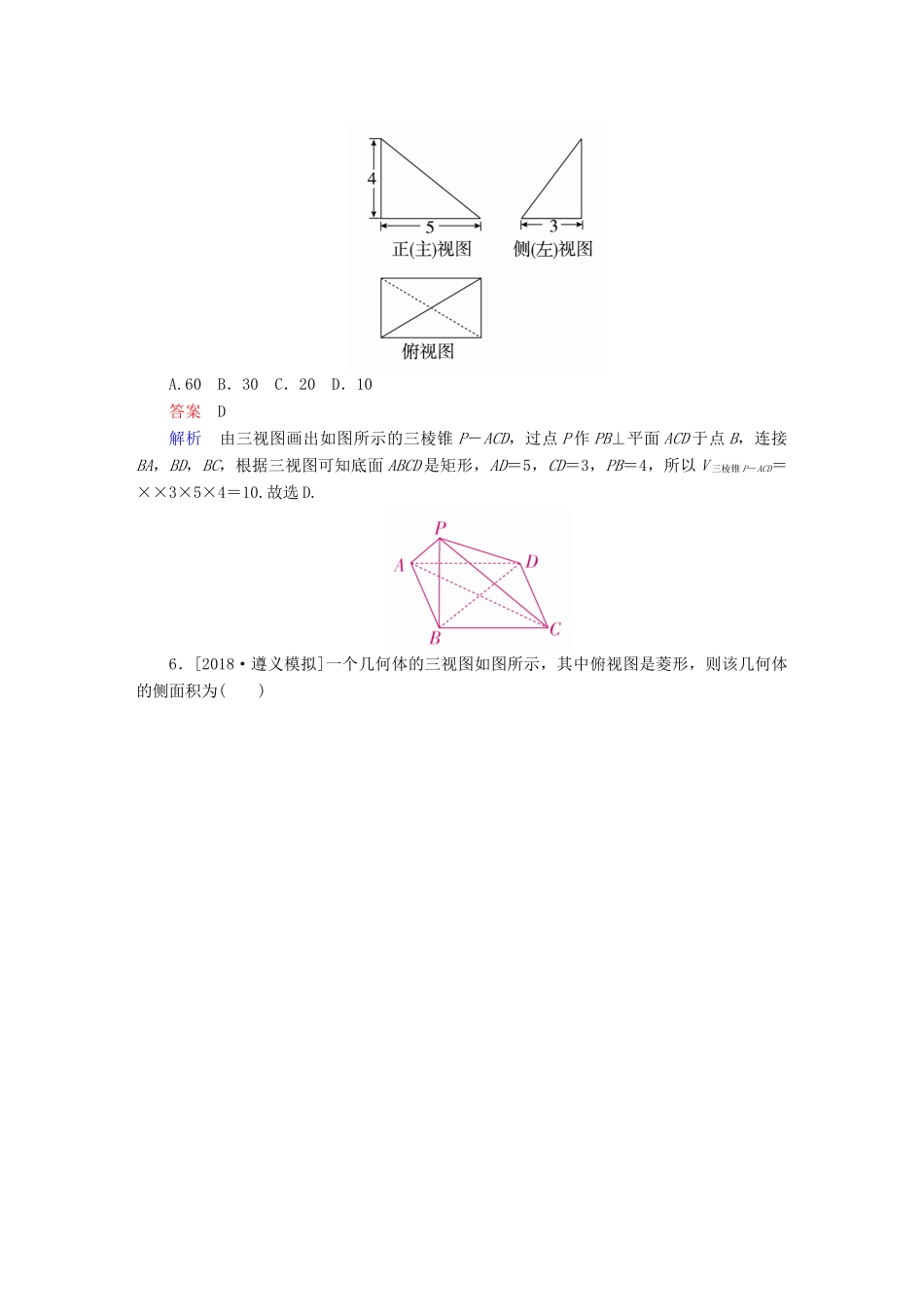
第2讲空间几何体的表面积和体积板块四模拟演练·提能增分[A级基础达标]1.[2018·南昌模拟]如图,在正四棱柱ABCD-A1B1C1D1中,点P是平面A1B1C1D1内一点,则三棱锥P-BCD的正视图与侧视图的面积之比为()A.1∶1B.2∶1C.2∶3D.3∶2答案A解析根据题意,三棱锥P-BCD的正视图是三角形,且底边为正四棱柱的底面边长、高为正四棱柱的高;侧视图是三角形,且底边为正四棱柱的底面边长、高为正四棱柱的高.故三棱锥P-BCD的正视图与侧视图的面积之比为1∶1.故选A.2.《九章算术》商功章有题:一圆柱形谷仓,高1丈3尺3寸,容纳米2000斛(1丈=10尺,1尺=10寸,斛为容积单位,1斛≈1.62立方尺,π≈3),则圆柱底面圆周长约为()A.1丈3尺B.5丈4尺C.9丈2尺D.48丈6尺答案B解析设圆柱底面圆半径为r尺,高为h尺,依题意,圆柱体积为V=πr2h=2000×1.62≈3×r2×13.33,所以r2≈81,即r≈9,所以圆柱底面圆周长为2πr≈54,54尺=5丈4尺,则圆柱底面圆周长约为5丈4尺.故选B.3.某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.答案D解析由三视图,可得原图如图所示,即为底面是平行四边形的四棱锥,∴V=×1×1×1=.故选D.4.正三棱柱的底面边长为,侧棱长为2,且三棱柱的顶点都在同一个球面上,则该球的表面积为()A.4πB.8πC.12πD.16π答案B解析由正弦定理得=2r(其中r为正三棱柱底面三角形外接圆的半径),∴r=1,∴外接球的半径R==,∴外接球的表面积S=4πR2=8π.故选B.5.[2017·北京高考]某三棱锥的三视图如图所示,则该三棱锥的体积为()A.60B.30C.20D.10答案D解析由三视图画出如图所示的三棱锥P-ACD,过点P作PB⊥平面ACD于点B,连接BA,BD,BC,根据三视图可知底面ABCD是矩形,AD=5,CD=3,PB=4,所以V三棱锥P-ACD=××3×5×4=10.故选D.6.[2018·遵义模拟]一个几何体的三视图如图所示,其中俯视图是菱形,则该几何体的侧面积为()A.+B.+C.+D.+答案C解析由三视图还原为空间几何体,如图所示,则有OA=OB=1,AB=.又PB⊥平面ABCD,∴PB⊥BD,PB⊥AB,∴PD==,PA==,从而有PA2+DA2=PD2,∴PA⊥DA,∴该几何体的侧面积S=2×××1+2×××=+.故选C.7.某几何体的三视图如图所示,则其体积为()A.207B.216-C.216-36πD.216-18π答案B解析由已知三视图知该几何体为一个棱长为6的正方体,切去一个底面半径为3,高为6的圆锥.其体积V=63-××π×32×6=216-.故选B.8.[2017·江苏高考]如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的体积为V1,球O的体积为V2,则的值是________.答案解析设球O的半径为R, 球O与圆柱O1O2的上、下底面及母线均相切,∴圆柱O1O2的高为2R,圆柱O1O2的底面半径为R.∴==.9.某几何体的三视图如图所示,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是________.答案2(π+)解析由三视图可知此几何体的表面积分为两部分:底面积即俯视图的面积为2;侧面积为一个完整的圆锥的侧面积,且圆锥的母线长为2,底面半径为1,所以侧面积为2π.两部分加起来即为几何体的表面积,为2(π+).10.[2018·云南昆明联考]已知某几何体的三视图如图所示,则该几何体的体积等于________.答案解析由三视图可知该几何体是一个直三棱柱切去一个三棱锥,如图所示,故该几何体的体积为×4×4×8-××4×4×4=64-=.[B级知能提升]1.[2018·上海模拟]如图是某几何体的三视图,则此几何体的体积是()A.B.C.D.答案D解析根据三视图知此几何体是边长为2的正方体截去一个三棱锥P-ABC剩下的部分(如图所示),所以此几何体的体积为2×2×2-××1×2×2=.故选D.2.[2018·北京模拟]某三棱锥的三视图如图所示,则该三棱锥的表面积是()A.2+B.4+C.2+2D.5答案C解析由三视图分析知,该几何体是底面为等腰三角形,其中一条侧棱与底面垂直的三棱锥(SA⊥平面ABC),如图,由三视图中的数据可计算得S△ABC=×2×2=2,S△SAC=××1=,S△SAB=××1=,S△SBC=×2×=,所以S表面积=2+2.故选C.3.[2017·全国卷Ⅰ]已知三棱锥S-ABC的所有顶点都在球O的球面上,SC...