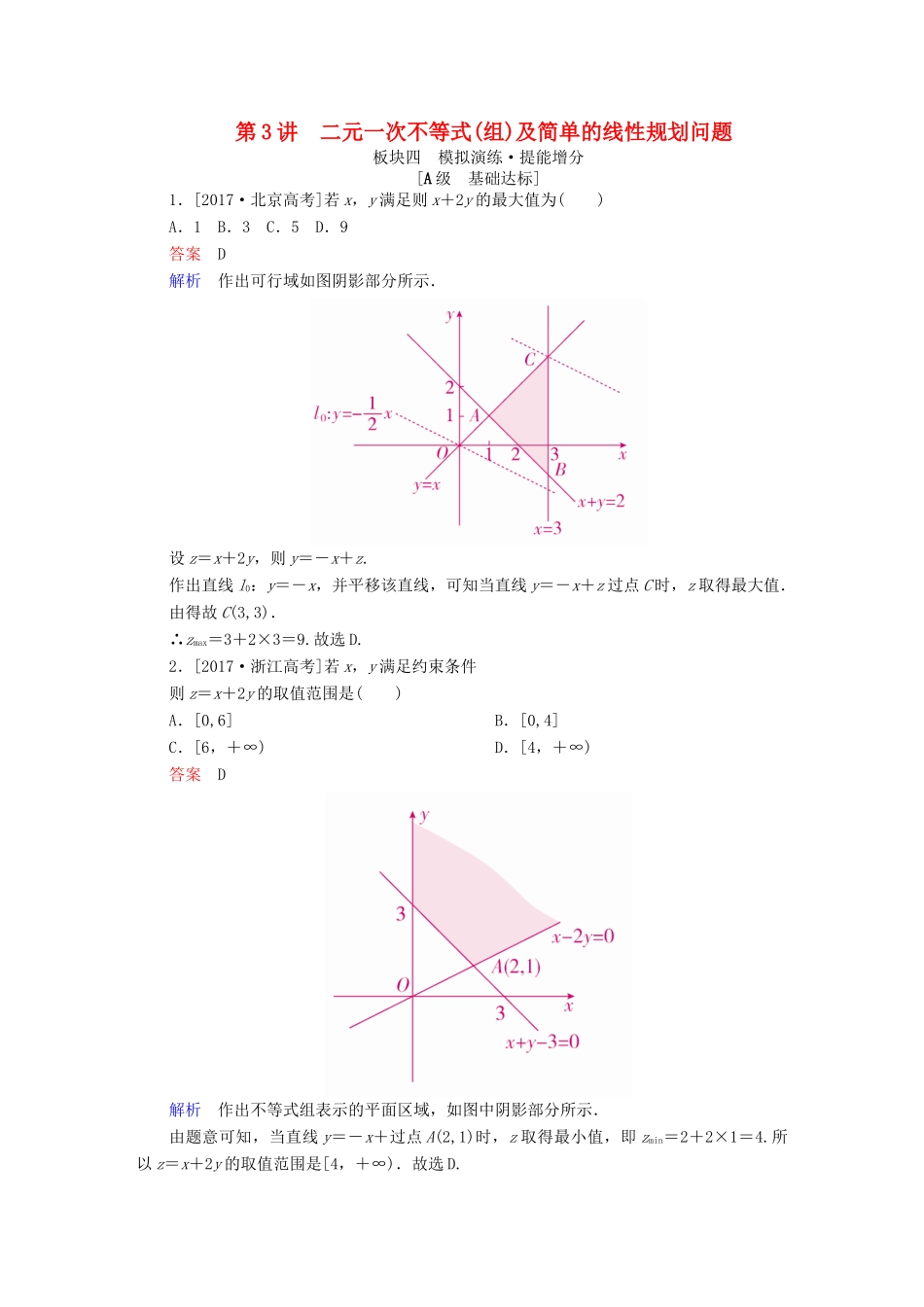
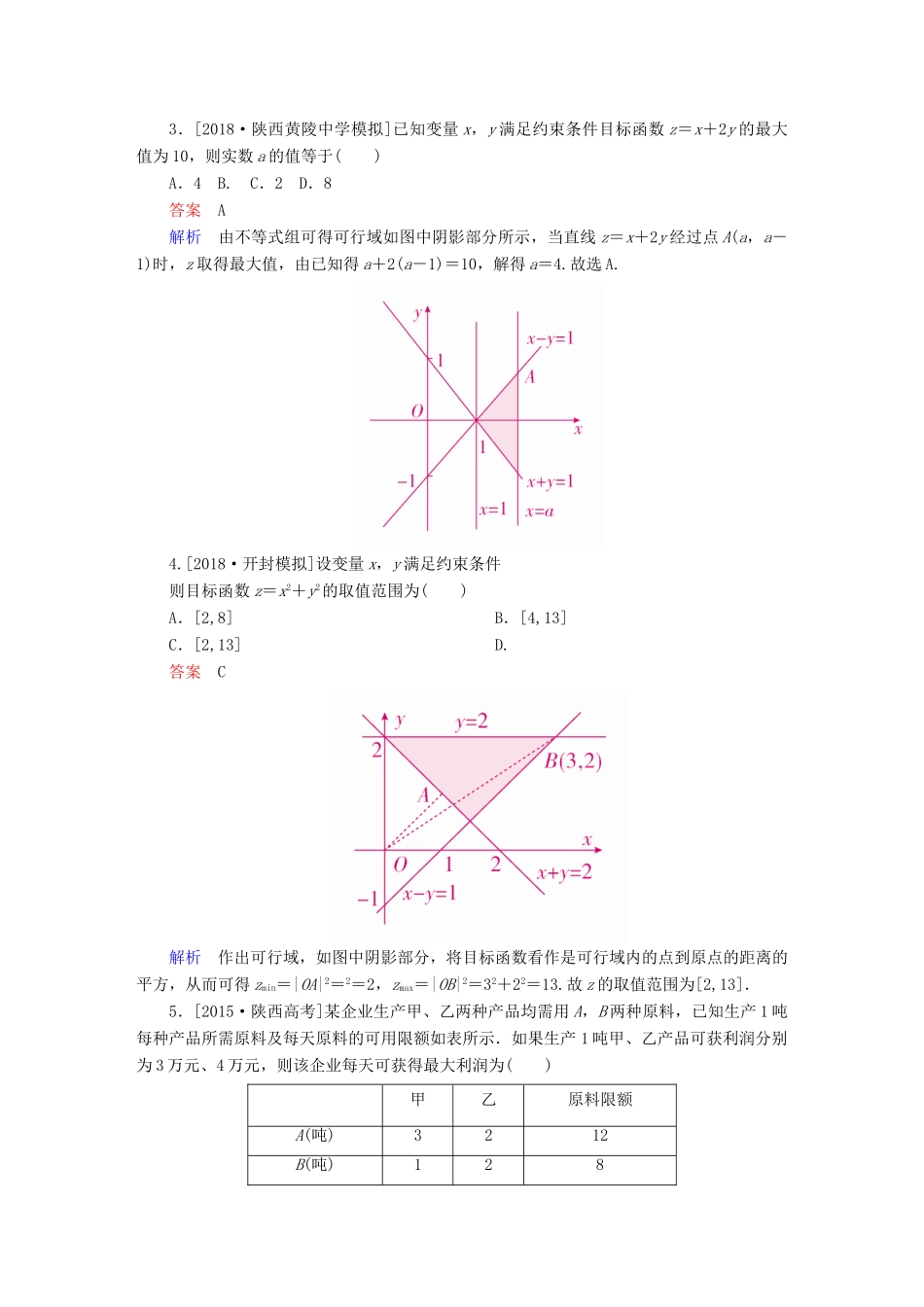
第3讲二元一次不等式(组)及简单的线性规划问题板块四模拟演练·提能增分[A级基础达标]1.[2017·北京高考]若x,y满足则x+2y的最大值为()A.1B.3C.5D.9答案D解析作出可行域如图阴影部分所示.设z=x+2y,则y=-x+z.作出直线l0:y=-x,并平移该直线,可知当直线y=-x+z过点C时,z取得最大值.由得故C(3,3).∴zmax=3+2×3=9.故选D.2.[2017·浙江高考]若x,y满足约束条件则z=x+2y的取值范围是()A.[0,6]B.[0,4]C.[6,+∞)D.[4,+∞)答案D解析作出不等式组表示的平面区域,如图中阴影部分所示.由题意可知,当直线y=-x+过点A(2,1)时,z取得最小值,即zmin=2+2×1=4.所以z=x+2y的取值范围是[4,+∞).故选D.3.[2018·陕西黄陵中学模拟]已知变量x,y满足约束条件目标函数z=x+2y的最大值为10,则实数a的值等于()A.4B.C.2D.8答案A解析由不等式组可得可行域如图中阴影部分所示,当直线z=x+2y经过点A(a,a-1)时,z取得最大值,由已知得a+2(a-1)=10,解得a=4.故选A.4.[2018·开封模拟]设变量x,y满足约束条件则目标函数z=x2+y2的取值范围为()A.[2,8]B.[4,13]C.[2,13]D.答案C解析作出可行域,如图中阴影部分,将目标函数看作是可行域内的点到原点的距离的平方,从而可得zmin=|OA|2=2=2,zmax=|OB|2=32+22=13.故z的取值范围为[2,13].5.[2015·陕西高考]某企业生产甲、乙两种产品均需用A,B两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为()甲乙原料限额A(吨)3212B(吨)128A.12万元B.16万元C.17万元D.18万元答案D解析设该企业每天生产甲产品x吨,乙产品y吨,获利z元.则由题意知利润函数z=3x+4y.画出可行域如图所示,当直线3x+4y-z=0过点B时,目标函数取得最大值.由解得故利润函数的最大值为z=3×2+4×3=18(万元).故选D.6.某校今年计划招聘女教师a名,男教师b名,若a,b满足不等式组设这所学校今年计划招聘教师最多x名,则x=()A.10B.12C.13D.16答案C解析画出约束条件所表示的区域,即可行域,如图阴影部分所示,作直线l:b+a=0,平移直线l,再由a,b∈N,可知当a=6,b=7时,x=a+b=13.故选C.7.[2017·全国卷Ⅰ]设x,y满足约束条件则z=3x-2y的最小值为________.答案-5解析作出可行域如图阴影部分所示.由z=3x-2y,得y=x-.作出直线l0:y=x,并平移l0,知当直线y=x-过点A时,z取得最小值.由得A(-1,1),∴zmin=3×(-1)-2×1=-5.8.[2018·辽宁模拟]设变量x,y满足则2x+3y的最大值为________.答案55解析不等式组表示的区域如图所示,令z=2x+3y,目标函数变为y=-x+,因此截距越大,z的取值越大,故当直线z=2x+3y经过点A时,z最大,由于⇒故点A的坐标为(5,15),代入z=2x+3y,得到zmax=55,即2x+3y的最大值为55.9.已知变量x,y满足约束条件且有无穷多个点(x,y)使目标函数z=x+my取得最小值,求m的值.解作出线性约束条件表示的平面区域,如图中阴影部分所示.若m=0,则z=x,目标函数z=x+my取得最小值的最优解只有一个,不符合题意.若m≠0,则目标函数z=x+my可看作斜率为-的动直线y=-x+,若m<0,则->0,数形结合知使目标函数z=x+my取得最小值的最优解不可能有无穷多个;若m>0,则-<0,数形结合可知,当动直线与直线AB重合时,有无穷多个点(x,y),在线段AB上,使目标函数z=x+my取得最小值,即-=-1,则m=1.综上可知,m=1.10.变量x,y满足(1)设z=,求z的最小值;(2)设z=x2+y2,求z的取值范围;(3)设z=x2+y2+6x-4y+13,求z的取值范围.解由约束条件作出(x,y)的可行域如图所示.由解得A.由解得C(1,1).由解得B(5,2).(1)因为z==,所以z的值即是可行域中的点与原点O连线的斜率.观察图形可知zmin=kOB=.(2)z=x2+y2的几何意义是可行域上的点到原点O的距离的平方.结合图形可知,可行域上的点到原点的距离中,dmin=|OC|=,dmax=|OB|=.所以2≤z≤29.(3)z=x2+y2+6x-4y+13=(x+3)2+(y-2)2的几何意义是可行域上的点到点(-3,2)的距...