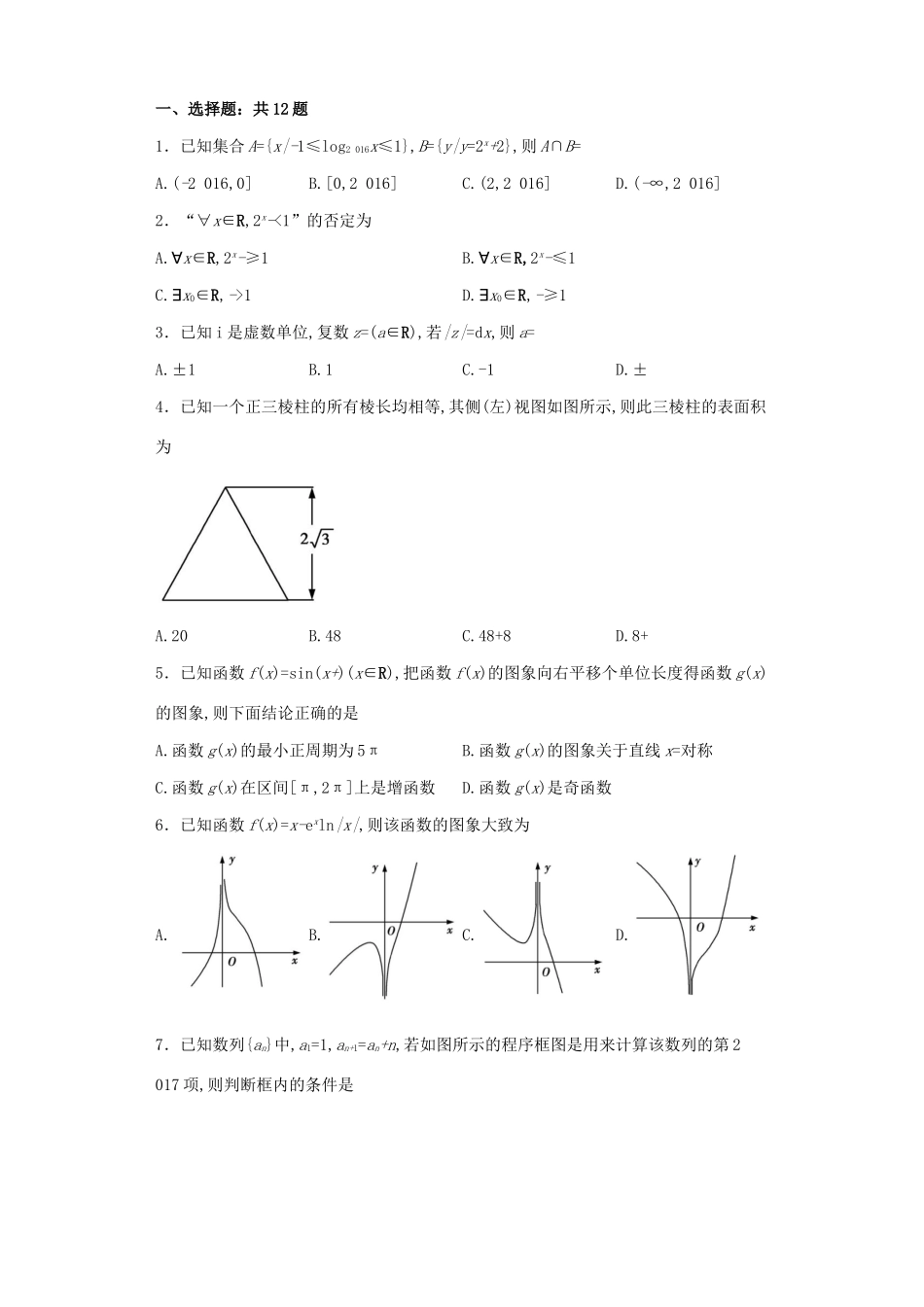
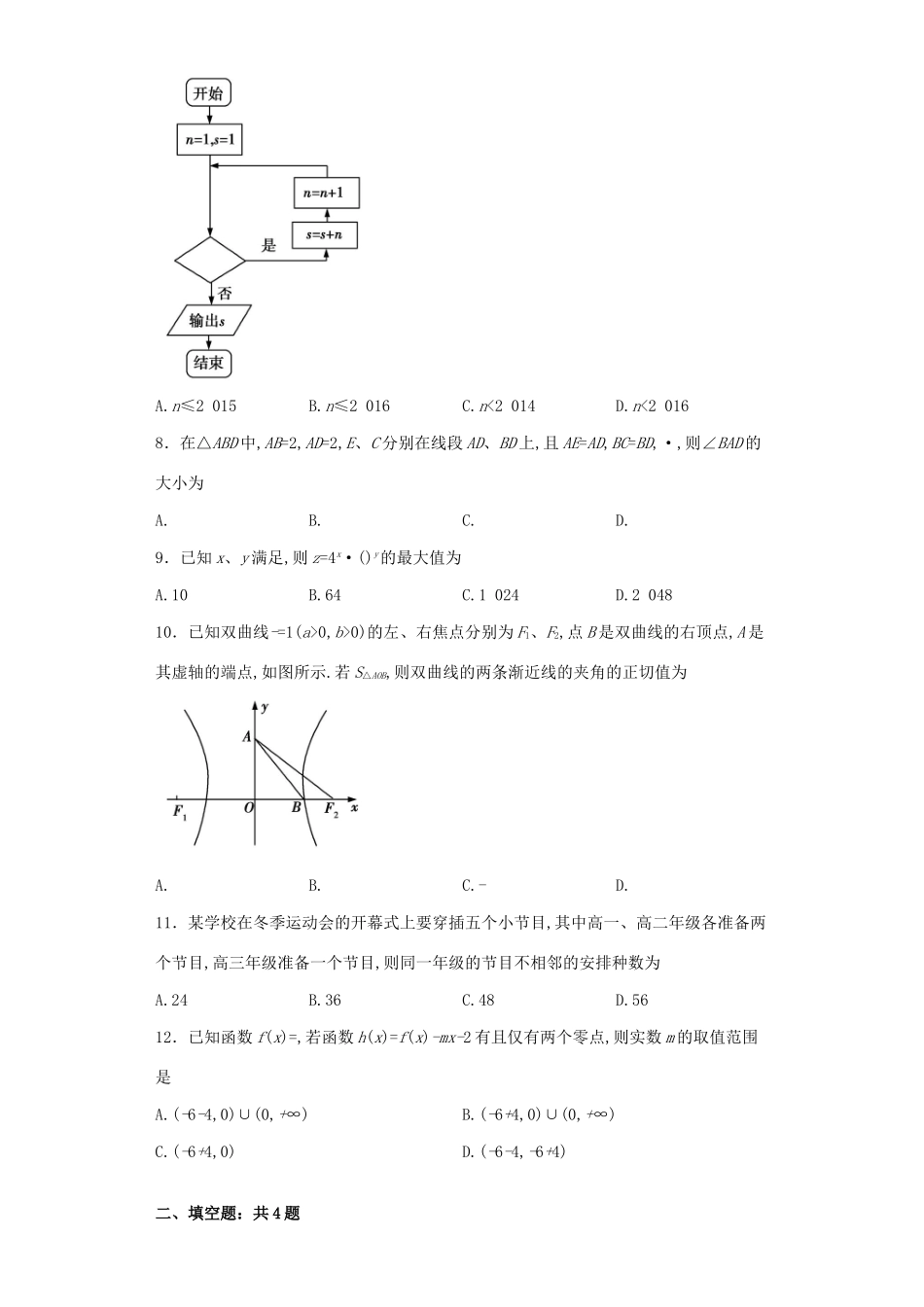
一、选择题:共12题1.已知集合A={x|-1≤log2016x≤1},B={y|y=2x+2},则A∩B=A.(-2016,0]B.[0,2016]C.(2,2016]D.(-∞,2016]2.“∀x∈R,2x-<1”的否定为A.∀x∈R,2x-≥1B.∀x∈R,2x-≤1C.∃x0∈R,->1D.∃x0∈R,-≥13.已知i是虚数单位,复数z=(a∈R),若|z|=dx,则a=A.±1B.1C.-1D.±4.已知一个正三棱柱的所有棱长均相等,其侧(左)视图如图所示,则此三棱柱的表面积为A.20B.48C.48+8D.8+5.已知函数f(x)=sin(x+)(x∈R),把函数f(x)的图象向右平移个单位长度得函数g(x)的图象,则下面结论正确的是A.函数g(x)的最小正周期为5πB.函数g(x)的图象关于直线x=对称C.函数g(x)在区间[π,2π]上是增函数D.函数g(x)是奇函数6.已知函数f(x)=x-exln|x|,则该函数的图象大致为A.B.C.D.7.已知数列{an}中,a1=1,an+1=an+n,若如图所示的程序框图是用来计算该数列的第2017项,则判断框内的条件是A.n≤2015B.n≤2016C.n<2014D.n<20168.在△ABD中,AB=2,AD=2,E、C分别在线段AD、BD上,且AE=AD,BC=BD,·,则∠BAD的大小为A.B.C.D.9.已知x、y满足,则z=4x·()y的最大值为A.10B.64C.1024D.204810.已知双曲线-=1(a>0,b>0)的左、右焦点分别为F1、F2,点B是双曲线的右顶点,A是其虚轴的端点,如图所示.若S△AOB,则双曲线的两条渐近线的夹角的正切值为A.B.C.-D.11.某学校在冬季运动会的开幕式上要穿插五个小节目,其中高一、高二年级各准备两个节目,高三年级准备一个节目,则同一年级的节目不相邻的安排种数为A.24B.36C.48D.5612.已知函数f(x)=,若函数h(x)=f(x)-mx-2有且仅有两个零点,则实数m的取值范围是A.(-6-4,0)∪(0,+∞)B.(-6+4,0)∪(0,+∞)C.(-6+4,0)D.(-6-4,-6+4)二、填空题:共4题13.已知幂函数y=xa过点(4,16),则(x-)8的展开式中x2的系数为.14.已知直线及直线截圆C所得的弦长均为8,则圆C的面积是.15.在正三棱锥P-ABC中,M是PC的中点,且AM⊥PB,AB=2,则正三棱锥P-ABC的外接球的表面积为.16.在△ABC中,角A、B、C所对的边分别为a、b、c,且满足cos2B+sin2B=1,0b>0)的离心率为,左焦点F1到点P(2,1)的距离为.(1)求椭圆的标准方程;(2)过椭圆右焦点F2的直线l与椭圆交于不同的两点M,N,则△F1MN内切圆的面积是否存在最大值?若存在,求出这个最大值及此时直线l的方程;若不存在,请说明理由.21.已知函数F(x)=ax2-xlnx,f(x)=F'(x)+1,g(x)=-(a∈R).(1)当a=g'(1)时,求曲线y=f(x)在(e,f(e))(e是自然对数的底数)处的切线方程;(2)当x∈(0,e]时,是否存在实数a,使得f(x)的最小值是3?若存在,求出a的值;若不存在,请说明理由.22.如图,已知四边形ABCD内接于圆O,且AB是圆O的直径,以点D为切点的圆O的切线与BA的延长线交于点M.(1)若MD=6,MB=12,求AB的长;(2)若AM=AD,求∠DCB的大小.23.在直角坐标系xOy中,曲线C1的参数方程是(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρsin(θ+)=1.(1)求曲线C1的普通方程与曲线C2的直角坐标方程;(2)求两曲线交点间的距离.24.已知函数f(x)=|x+2|.(1)解关于x的不等式f(x)-|3x-4|≤1;(2)若f(x)+|x-a|>1恒成立,求实数a的取值范围.参考答案1.C【解析】本题主要考查对数不等式的解法、指数函数的值域、集合的运算.先化简集合A、B,再求A∩B.由已知得A={x|≤x≤2016},B={y|y>2},所以A∩B=(2,2016].2.D【解析】本题考查全称命题的否定,根据全称命题的否定...