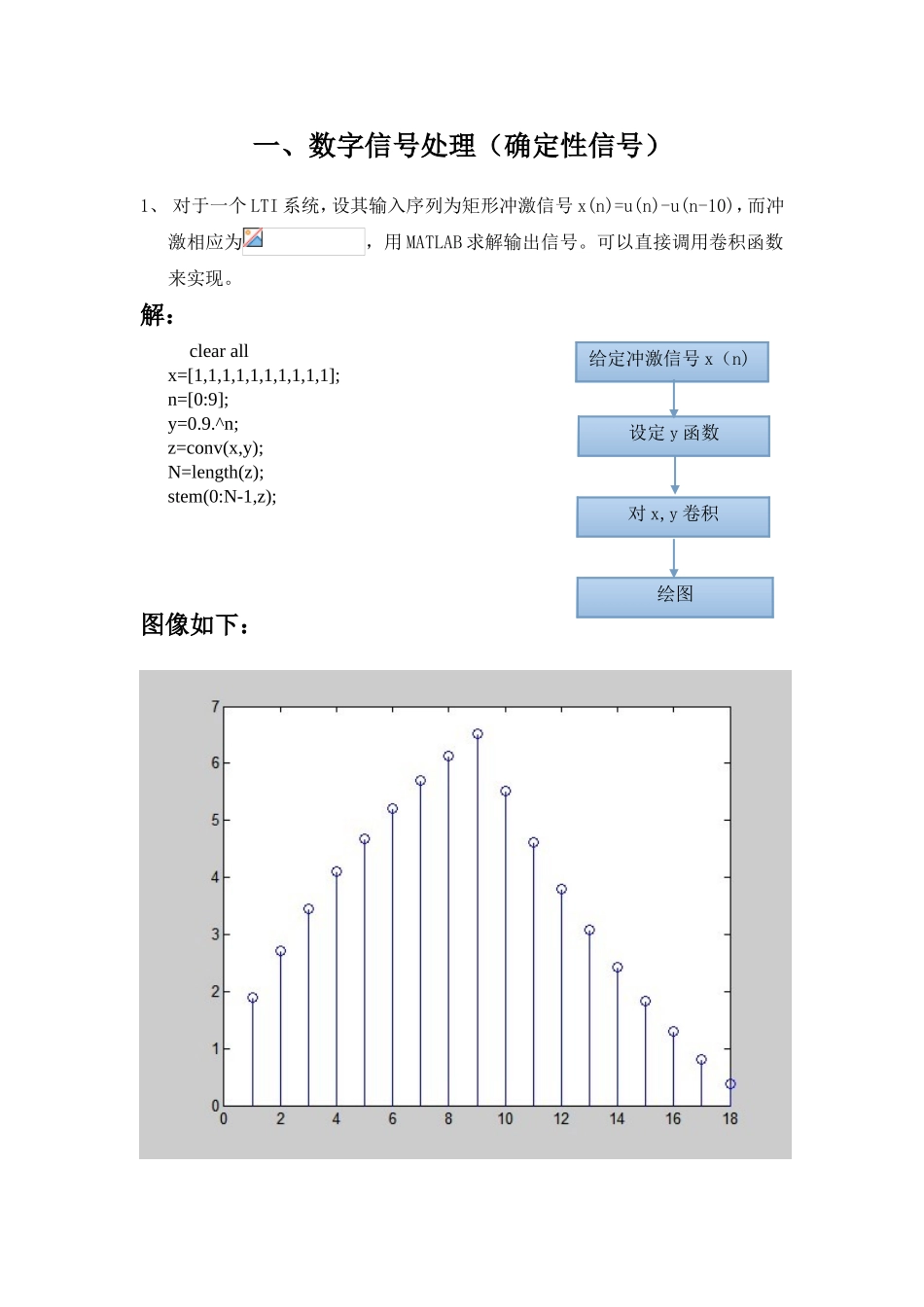
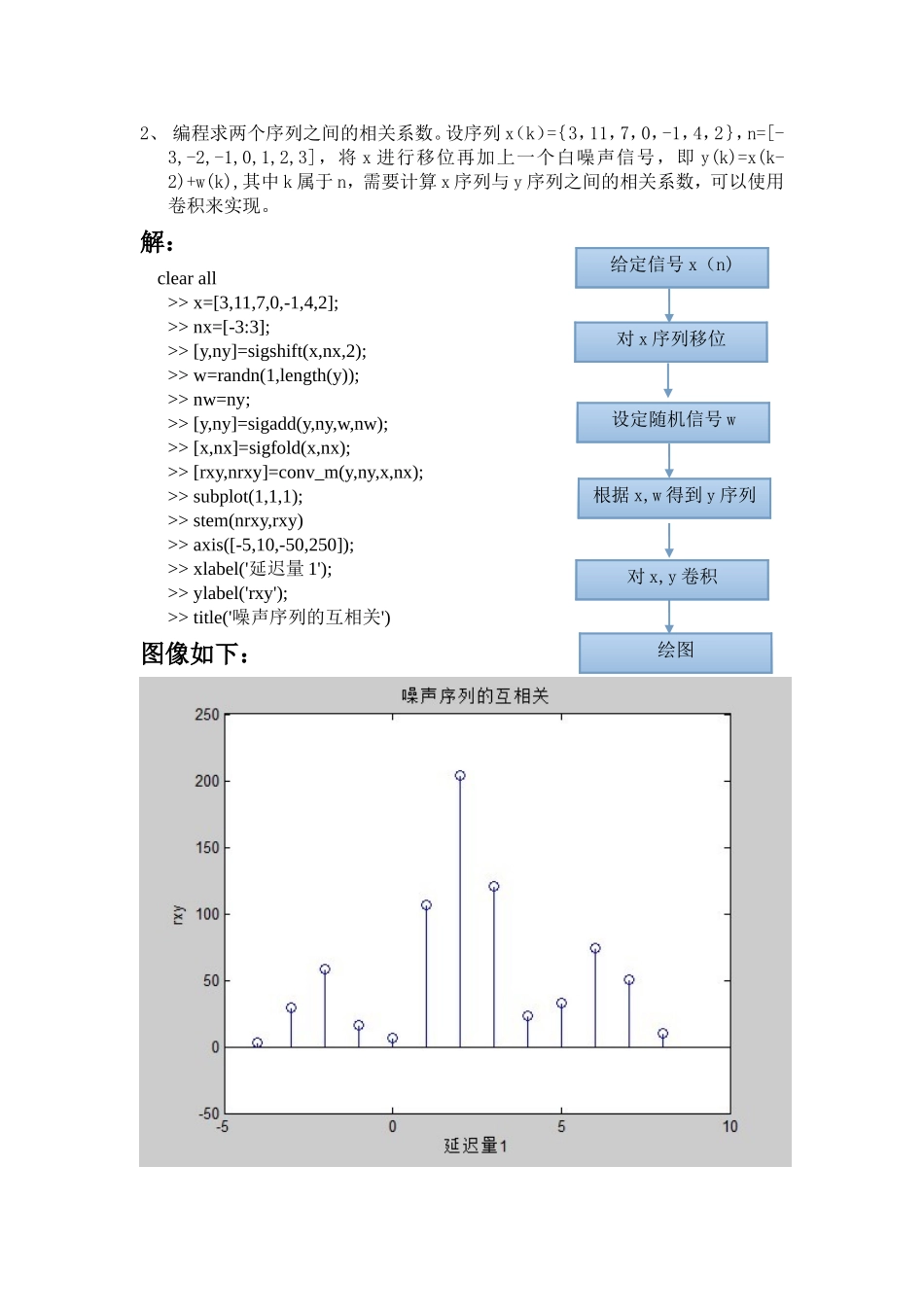
一、数字信号处理(确定性信号)1、对于一个LTI系统,设其输入序列为矩形冲激信号x(n)=u(n)-u(n-10),而冲激相应为,用MATLAB求解输出信号。可以直接调用卷积函数来实现。解:clearallx=[1,1,1,1,1,1,1,1,1,1];n=[0:9];y=0.9.^n;z=conv(x,y);N=length(z);stem(0:N-1,z);图像如下:给定冲激信号x(n)设定y函数绘图对x,y卷积2、编程求两个序列之间的相关系数。设序列x(k)={3,11,7,0,-1,4,2},n=[-3,-2,-1,0,1,2,3],将x进行移位再加上一个白噪声信号,即y(k)=x(k-2)+w(k),其中k属于n,需要计算x序列与y序列之间的相关系数,可以使用卷积来实现。解:clearall>>x=[3,11,7,0,-1,4,2];>>nx=[-3:3];>>[y,ny]=sigshift(x,nx,2);>>w=randn(1,length(y));>>nw=ny;>>[y,ny]=sigadd(y,ny,w,nw);>>[x,nx]=sigfold(x,nx);>>[rxy,nrxy]=conv_m(y,ny,x,nx);>>subplot(1,1,1);>>stem(nrxy,rxy)>>axis([-5,10,-50,250]);>>xlabel('延迟量1');>>ylabel('rxy');>>title('噪声序列的互相关')图像如下:给定信号x(n)对x序列移位设定随机信号w根据x,w得到y序列对x,y卷积绘图3、利用filter函数计算冲激相应和单位阶跃响应。设离散系统由下列差分方程表示:。解:冲激响应:clearalla1=[1,-1,0.9];b1=[1];n=0:100;x1=[1zeros(1,100)];%补零y1filter=filter(b1,a1,x1);stem(n,y1filter);title('冲激响应');xlabel('x');ylabel('y');阶跃响应:clearalla1=[1,-1,0.9];b1=[1];n=0:100;x2=ones(1,101);%全一矩阵y1filter=filter(b1,a1,x2);stem(n,y1filter);title('阶跃响应');xlabel('x');ylabel('y');图像如下:由差分方程确定系数组给定输入x利用filter函数计算绘图4、编程求解有限时宽复指数序列,n=[0,10]的频谱及能量谱。解:n=0:10;x=(0.9*exp(j*pi/3)).^n;k=-200:200;w=(pi/100)*k;X=x*(exp(-j*pi/100)).^(n'*k);magX=abs(X);angX=angle(X);subplot(2,1,1);plot(w/pi,magX);gridxlabel('以w/pi为单位的频率');ylabel('|X|')title('幅度部分')subplot(2,1,2);plot(w/pi,angX/pi);gridxlabel('以w/pi为单位的频率');ylabel('弧度/pi')title('相角部分')figure;Y=sum(abs(x).^2);stem(Y);title('能量谱');给定信号x(n)对x进行离散时间傅里叶变换得到X设定X的幅值和相角函数绘图图像如下:5、已知信号,随机正态白噪声为的均值为0,标准误差为1。试比较采样点数分别为45、64点时的频谱(幅度谱)图像的差异。解:clearall;fs=100;N=45;n=0:N-1;t=n/fs;x=2*sin(4*pi*t)+5*cos(8*pi*t);y=x+randn(size(x));X=fft(y,N);magX=abs(X);f=n*fs/N;subplot(2,1,1);plot(f,magX);xlabel('频率Hz');ylabel('45点幅度谱');clearall;fs=100;N=64;n=0:N-1;t=n/fs;x=2*sin(2*pi*2*t)+5*cos(2*pi*4*t);y=x+randn(size(x));X=fft(y,N);magX=abs(X);f=n*fs/N;subplot(2,1,2);plot(f,magX);xlabel('频率Hz');ylabel('64点幅度谱');给定信号x(n)及采样频率设定随机信号w绘制频谱图根据x,w得到y信号对y快速傅里叶变换6、设序列,分别考虑n=[0,10]和n=[0,100]两种情况频谱特征。对比当n=[0,10]时,取10点及取100点(补90个0点)时情况,并说明高密度和高分辨率频谱之间的差异。解:clearall;n=[0:100];x=cos(0.48*pi*n)+cos(0.52*pi*n);n1=[0:10];x1=x(1:1:10);Y1=fft(x1,10);magY1=abs(Y1);subplot(3,1,1);plot(magY1);title('10点的幅度谱');n2=[0:100];x2=[x(1:1:10),zeros(1,90)];Y2=fft(x2,100);magY2=abs(Y2);subplot(3,1,2);plot(magY2);title('补90个0的幅度谱(高密度)');n3=[0:100];x3=x(1:1:100);Y3=fft(x3,100);magY3=abs(Y3);subplot(3,1,3);plot(magY3);title('100点的幅度谱(高分辨率)');给定信号x分别设定三种情况的点数绘制频谱图比较差异图像如下:7、设计具有下列指标的低通FIR滤波器:通带截频,阻带截频,通带波动dB,最小的阻带衰减dB。解:wp=0.2*pi;ws=0.3*pi;tr_width=ws-wp%过渡带宽M=ceil(6.6*pi/tr_width)+1n=[0:1:M-1];wc=(ws+wp)/2,%理想LPF截止频率hd=ideal_lp(wc,M);%理想低通滤波器的单位冲激响应w_ham=(hamming(M))';h=hd.*w_ham;%截取得到实际的单位脉冲响应[db,mag,pha,grd,w...