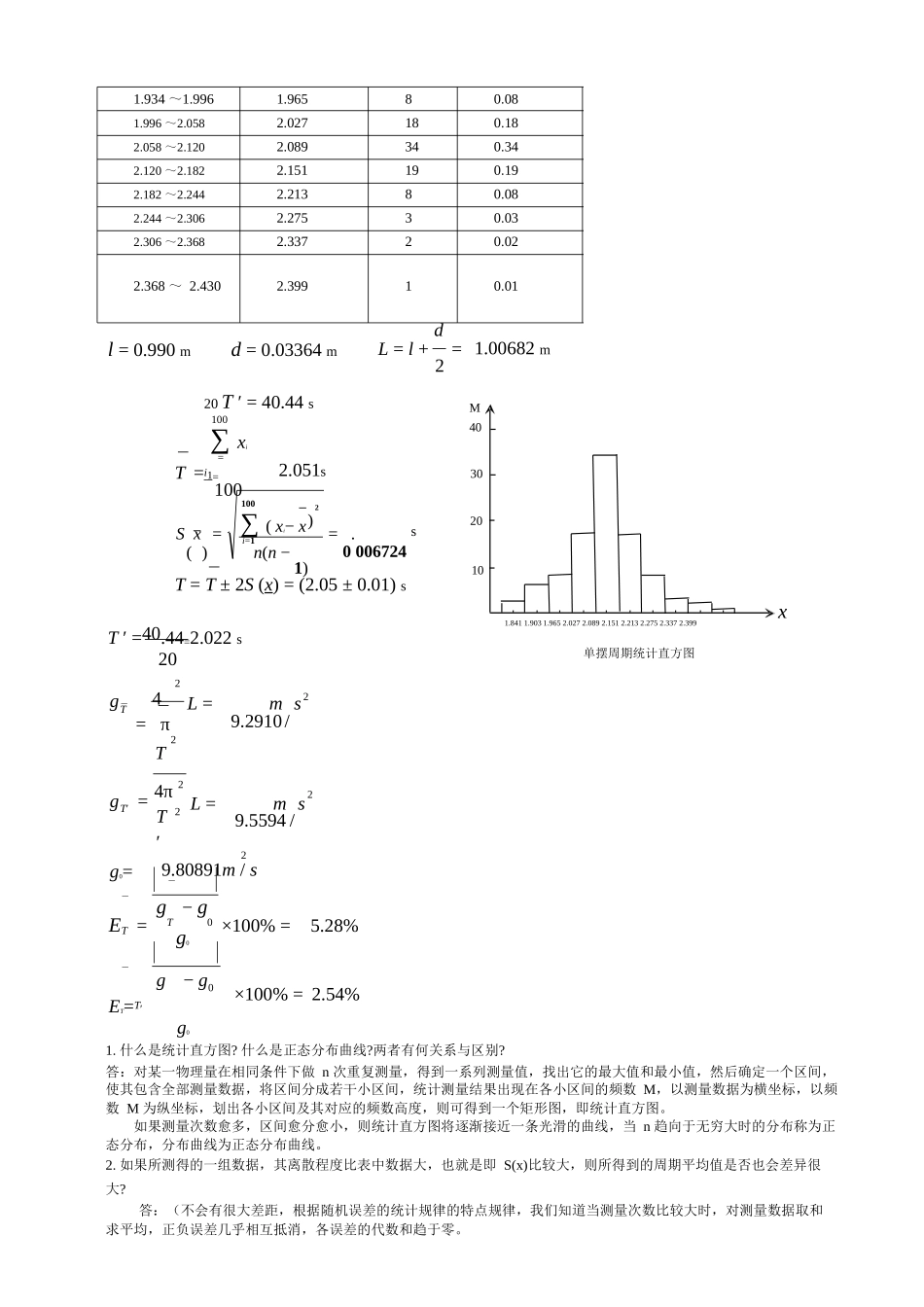
随机误差的统计规律实验目的(1)通过一些简单测量,加深对随机误差统计规律的认识(2)学习正确估算随机误差、正确表达直接测量结果的一般方法(3)了解运用统计方法研究物理现象的简单过程实验方法原理对某一物理量在相同条件下进行n次重复测量(n>100),得到n个结果x1,x2,⋯,xn,先找出它的最小值和最大值,然后确定一个区间[x′,x′],使这个区间包含了全部测量数据。将区间[x′,x′]分成若干个小区间,比如Kx′−x′个,则每个小区间的间隔∆为∆=K,统计测量结果出现在各个小区间的次数M(称为频数)。以测量数据为横坐标,只需标明各区间的中点值,以频数M为纵坐标,画出各小区间及其对应的频数高度,则可得到一组矩形图,这就是统计直方图。直方图的包络表示频数的分布,它反映了测量数据的分布规律,也即随机误差的分布规律。实验步骤(1)用钢卷尺测量摆线长。(2)用游标卡尺测量摆球直径。(3)当摆长不变,摆角(小于5o)保持一定时,摆动的周期是一个恒量,用数字秒表测量单摆的周期至少100次,计算测量结果的平均值T和算术平均值的标准差S(x)。(4)保持摆长不变,一次测量20个以上全振动的时间间隔,算出振动周期。数据处理2.072.122.122.002.222.112.432.122.221.912.182.032.062.282.162.102.032.091.941.901.992.001.982.002.062.252.161.992.042.132.162.012.222.192.121.941.912.042.102.222.162.032.062.032.311.942.122.192.131.811.992.032.282.062.062.162.002.092.121.971.932.062.112.132.122.162.132.132.122.052.062.122.112.072.042.092.092.072.102.002.231.842.062.132.122.172.002.002.112.222.092.062.181.912.032.232.192.352.122.07小区间1.811~1.8721.872~1.934小区间中点值1.8411.093频数M25相对频数M/n0.020.051.934~1.9961.996~2.0582.058~2.1202.120~2.1822.182~2.2442.244~2.3062.306~2.3682.368~2.4301.9652.0272.0892.1512.2132.2752.3372.39981834198321d0.080.180.340.190.080.030.020.01l=0.990md=0.03364m20T′=40.44s100∑xi=L=l+=21.00682mM40T=i1=1001002.051s230Sx()=∑(xi−xi=1n(n−)=.0006724s201)T=T±2S(x)=(2.05±0.01)sT′=40.44=2.022s202101.8411.9031.9652.0272.0892.1512.2132.2752.3372.399单摆周期统计直方图xgT4=π2L=ms9.2910/2gT′=T4πT′22L=ms9.5594/22g0=9.80891m/sg−gET=Tg00×100%=5.28%g−gET=T′0×100%=2.54%g01.什么是统计直方图?什么是正态分布曲线?两者有何关系与区别?答:对某一物理量在相同条件下做n次重复测量,得到一系列测量值,找出它的最大值和最小值,然后确定一个区间,使其包含全部测量数据,将区间分成若干小区间,统计测量结果出现在各小区间的频数M,以测量数据为横坐标,以频数M为纵坐标,划出各小区间及其对应的频数高度,则可得到一个矩形图,即统计直方图。如果测量次数愈多,区间愈分愈小,则统计直方图将逐渐接近一条光滑的曲线,当n趋向于无穷大时的分布称为正态分布,分布曲线为正态分布曲线。2.如果所测得的一组数据,其离散程度比表中数据大,也就是即S(x)比较大,则所得到的周期平均值是否也会差异很大?答:(不会有很大差距,根据随机误差的统计规律的特点规律,我们知道当测量次数比较大时,对测量数据取和求平均,正负误差几乎相互抵消,各误差的代数和趋于零。3.测量凹透镜焦距f和实验室给出的f0,比较后计算出的E值(相对误差)一般比较大,试分析E大的原因?答:E较大的原因可能是因为放入凹透镜后所成像的清晰度很难确定,即像的聚焦情况不好,从而导致很难测出清晰成像的位置。4.在测量凸透镜的焦距时,可以利用测得的多组u、v值,然后以u+v作纵轴,以u·v作横轴,画出实验曲线。根据式(3-15-1)事先推断一下实验曲线将属于什么类型,怎样根据这条曲线求出透镜的焦距f?uυf=+答:曲线是直线,可根据直线的斜率求出f,f=1/k,因为1/f=1/u+1/v,即uυ,故可有f=1/k。5.测量凸透镜的焦距时,可以测得多组u、v值,以v/u(即像的放大率)作纵轴,以v作横轴,画出实验曲线。试问这条实验曲线具有什么形状?怎样由这条曲线求出透镜的焦距f?答:曲线是直线,在横轴上的截距就是f。