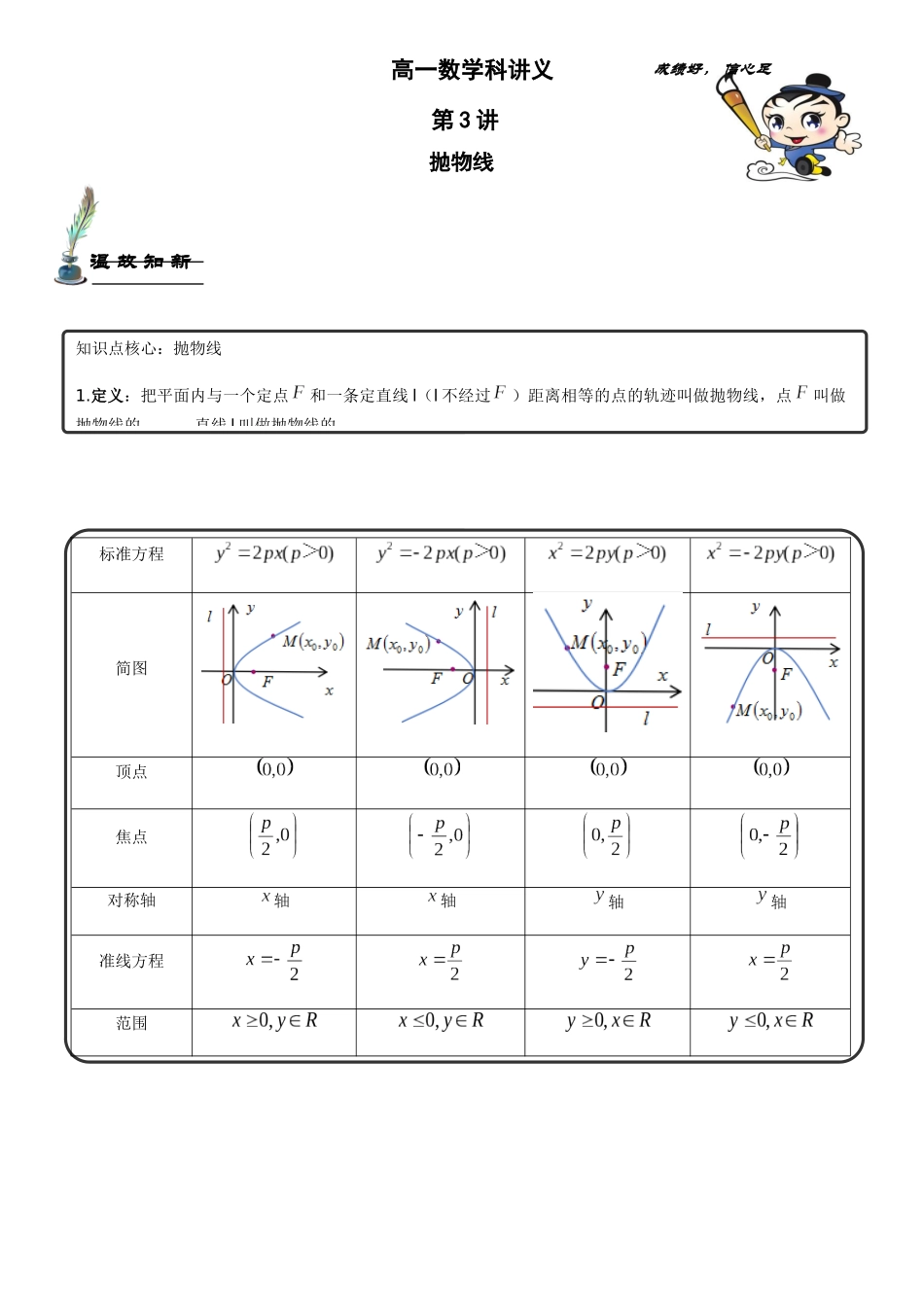
抛物线高一数学科讲义成绩好,信心足第3讲温故知新知识点核心:抛物线1.定义:把平面内与一个定点和一条定直线l(l不经过)距离相等的点的轨迹叫做抛物线,点叫做抛物线的______,直线l叫做抛物线的________。X≤0,无意义X>0,恒等于0标准方程简图顶点焦点对称轴轴轴轴轴准线方程范围抛物线定义中的“转化”法利用抛物线的定义解决此类问题,应灵活地进行抛物线上的点到焦点的距离与到准线距离的等价转化.“看到考点一:定义和标准方程抛物线焦点弦性质:直线过抛物线的焦点与抛物线交于两点(1)(2)(3)X≤0,无意义X>0,恒等于0准线想到焦点,看到焦点想到准线”,这是解决抛物线焦点弦有关问题的有效途径.[例1]设P是抛物线y2=4x上的一个动点.(1)求点P到点A(-1,1)的距离与点P到直线x=-1的距离之和的最小值;(2)若B(3,2),求|PB|+|PF|的最小值.变式1:已知抛物线的顶点在原点,对称轴是x轴,抛物线上的点M(-3,m)到焦点的距离等于5,求抛物线的方程和m的值.(1)关键:利用抛物线方程确定及应用其焦点、准线等性质时,关键是将抛物线方程化成标准方程.(2)技巧:要结合图形分析,灵活运用平面几何的性质以图助解.考点二:抛物线性质[例2]2_1(2013·四川高考)抛物线y2=4x的焦点到双曲线x2-=1的渐近线的距离是_____________.变式2:抛物线的焦点坐标是().(A)(B)(C)(D)变式3:抛物线2xy上一点到直线042yx的距离最短的点的坐标是()A.(1,1)B.(41,21)C.)49,23(D.(2,4)直线与抛物线相交的四个结论已知抛物线y2=2px(p>0),过其焦点的直线交抛物线于A,B两点,设A(x1,y1),B(x2,y2),则有以下结论:(1)|AB|=x1+x2+p或|AB|=(α为AB所在直线的倾斜角);(2)x1x2=;(3)y1y2=-p2;(4)过抛物线焦点且与对称轴垂直的弦称为抛物线的通径,抛物线的通径长为2p.[例3](2012·福建高考)如图,等边三角形OAB的边长为8,且其三个顶点均在抛物线E:x2=2py(p>0)上.(1)求抛物线E的方程;(2)设动直线l与抛物线E相切于点P,与直线y=-1相交于点Q.证明以PQ为直径的圆恒过y轴上某定点.考点三:抛物线与直线变式4:已知过点A(-4,0)的动直线l与抛物线G:x2=2py(p>0)相交于B,C两点.当直线l的斜率是时,=4.(1)求抛物线G的方程;(2)设线段BC的中垂线在y轴上的截距为b,求b的取值范围.1.抛物线是一种重要的圆锥曲线,在高考中,经常以抛物线为载体与直线、圆综合考查,主要考查抛物线的方程及几何性质,直线与抛物线的综合应用,点到直线的距离等.考点四:前沿热点2.直线与抛物线的综合问题,经常是将直线方程与抛物线方程联立,消去x(或y),利用方程的根与系数的关系求解,但一定要注意直线与抛物线相交的条件.[典例](2013·湖南高考)过抛物线E:x2=2py(p>0)的焦点F作斜率分别为k1,k2的两条不同直线l1,l2,且k1+k2=2,l1与E相交于点A,B,l2与E相交于点C,D,以AB,CD为直径的圆M,圆N(M,N为圆心)的公共弦所在直线记为l.(1)若k1>0,k2>0,证明:·<2p2;(2)若点M到直线l的距离的最小值为,求抛物线E的方程.变式5:(2013·广东高考)已知抛物线C的顶点为原点,其焦点F(0,c)(c>0)到直线l:x-y-2=0的距离为,设P为直线l上的点,过点P作抛物线C的两条切线PA,PB,其中A,B为切点.(1)求抛物线C的方程;(2)当点P(x0,y0)为直线l上的定点时,求直线AB的方程;(3)当点P在直线l上移动时,求|AF|·|BF|的最小值.变式6:已知直线y=-2上有一个动点Q,过点Q作直线l1垂直于x轴,动点P在l1上,且满足OP⊥OQ(O为坐标原点),记点P的轨迹为C.(1)求曲线C的方程;(2)若直线l2是曲线C的一条切线,当点(0,2)到直线l2的距离最短时,求直线l2的方程.课后练习:一、选择题(本大题共10小题,每小题5分,共50分)1.如果抛物线y2=ax的准线是直线x=-1,那么它的焦点坐标为()A.(1,0)B.(2,0)C.(3,0)D.(-1,0)2.圆心在抛物线y2=2x上,且与x轴和该抛物线的准线都相切的一个圆的方程是()A.x2+y2-x-2y-41=0B.x2+y2+x-2y+1=0C.x2+y2-x-2y+1=0D.x2+y2-x-2y+41=03.一抛物线形拱桥,当水面离桥顶2m时,水面宽4m,若水面下降1m,则水面宽为...