第一章概述 一简谐振动，振幅为0.20cm，周期为0.15s，求最大速度和加速度 练习题VIP免费

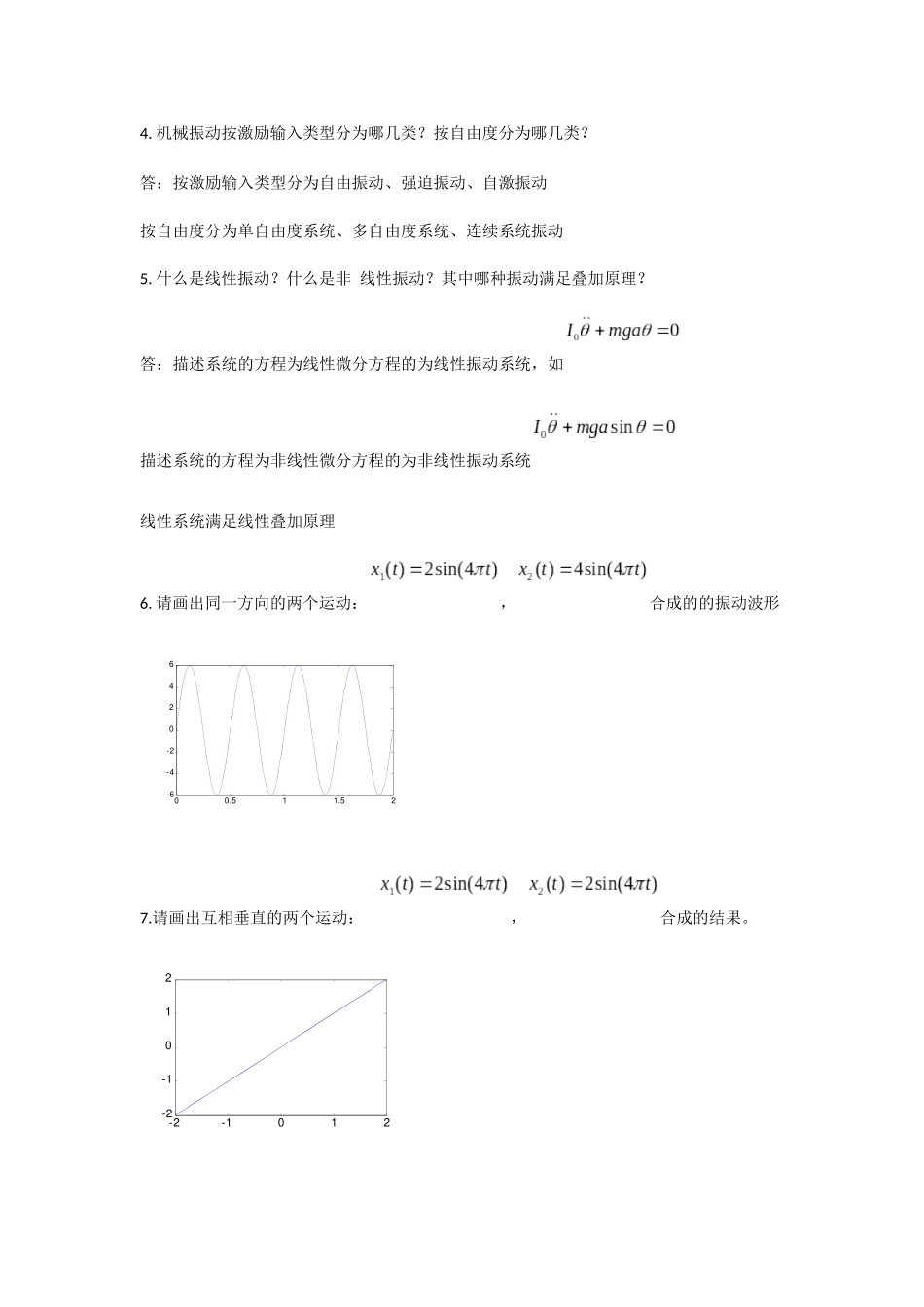
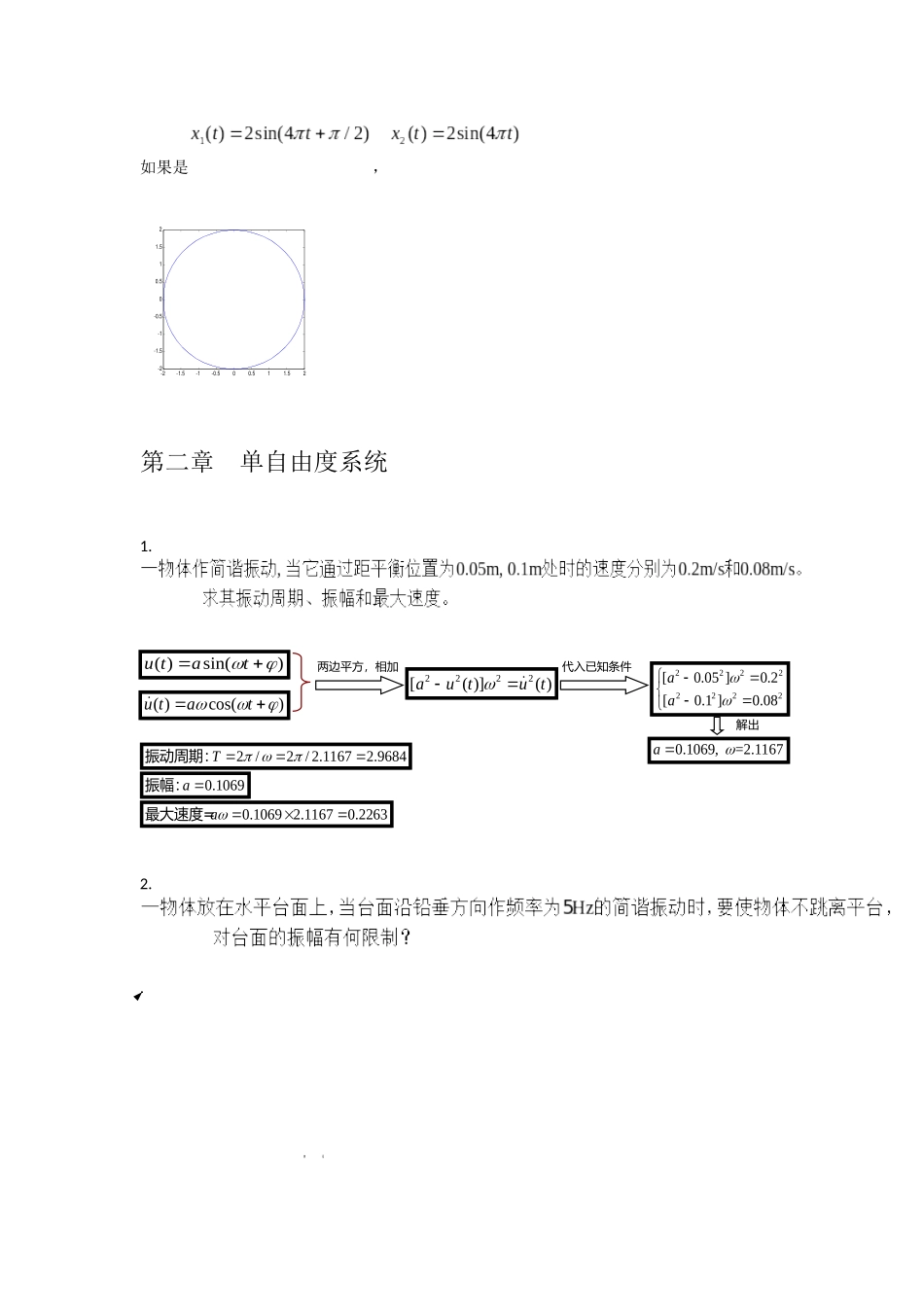
第一章概述1．一简谐振动，振幅为0.20cm，周期为0.15s，求最大速度和加速度。解：2．一加速度计指示结构谐振在80HZ时具有最大加速度50g，求振动的振幅。（g=10m/s2）解：3．一简谐振动，频率为10Hz，最大速度为4.57m/s，求谐振动的振幅、周期、最大加速度。解：4.机械振动按激励输入类型分为哪几类？按自由度分为哪几类？答：按激励输入类型分为自由振动、强迫振动、自激振动按自由度分为单自由度系统、多自由度系统、连续系统振动5.什么是线性振动？什么是非线性振动？其中哪种振动满足叠加原理？答：描述系统的方程为线性微分方程的为线性振动系统，如描述系统的方程为非线性微分方程的为非线性振动系统线性系统满足线性叠加原理6.请画出同一方向的两个运动：，合成的的振动波形00.511.52-6-4-202467.请画出互相垂直的两个运动：，合成的结果。-2-1012-2-1012如果是，-2-1.5-1-0.500.511.52-2-1.5-1-0.500.511.52第二章单自由度系统1.2.()sin()utat()cos()utat两边平方，相加2222[()]()autut代入已知条件22222222[0.05]0.2[0.1]0.08aa解出0.1069,=2.1167a2/2/2.11672.9684T振动周期：0.1069a振幅：0.10692.11670.2263a最大速度=mu123kkk分析表明：和并联，之后与串联1212eqkkkkk和并联后的等效刚度：31233123()eqeqeqkkkkkkkkkkk整个系统的等效刚度：261.86rad/seqnkm系统的固有频率：3.4.2()()utut()mNmgmut质量运动方程：()Nmutmg:0N不跳离条件()0mutmg2()gut2sin()gat()sin()0,t如果则上式恒成立2229.8()sin()0,9.9mmsin()(25)ggtat如果则上式变为Wv5.6.nkm系统固有频率：0(0)0,(0)uuv初始条件：220000()nnuvmauvk振幅：05410009.80.510004101.9810(N)Tmgkamgvmk最大张力：7.01112ln,ln,,lnnnAAAAAA010112ln()lnnnnAAAAnAAAA01ln2nAnA01ln2nAnA033222ln()106.4109.8ln()6.91(Ns/m)201.6100.01ssnsAmggmgcmkmmnA22220032321120()()22109.8((6.410)(1.610))0.19(NM)20.01nnsmgkAAAA周阻尼器消耗的能量8.9.10.0()()()sin()mutcutkutft0()()()jtmutcutkutfe()*()ddjtjjtddutBeBee稳态解：02djdfBekmjc222()01644llmglmlck2240.4919.87.14(rad/s)4410.49nklmgml22248160.2119.816()161(224)2()0.4944clcmgklmglmkmll10.212n位移共振：2211()2n21dn221()dn222nd系统固有频率：222221()2dndd阻尼比：2222222222222nddddcmmm阻尼系数：222211d振幅对数衰减率：11.12.2()()sinMutkutmet系统运动方程：*0()sinutft特解：220222nmemeMfkM2*22()sinnmeMutt稳态解：(1)求临界转速(2)1000rpm当转速为时，受迫振动的振幅。6310109.55(rad/s)250nkM临界转速nkM其中：220262200.01(104.72)0.0085(m)310250(104.72)mefkM受迫振动振幅：100021000(rpm)104.72(rad/s)6013.2220493sinmlclkllft20032sinsinnnftBtml3nkm23ckm()*()ddjtjjtddteee稳态解：202jtnnBe003fBml0222djdnnBej00222222||2()(2)dnnnnBBjnm当时质量的线位移幅值：0012222|4()(2)nndnnBfmullck/2nm当时质量的线位移幅值：002/222222/24|()(2)8164/()...