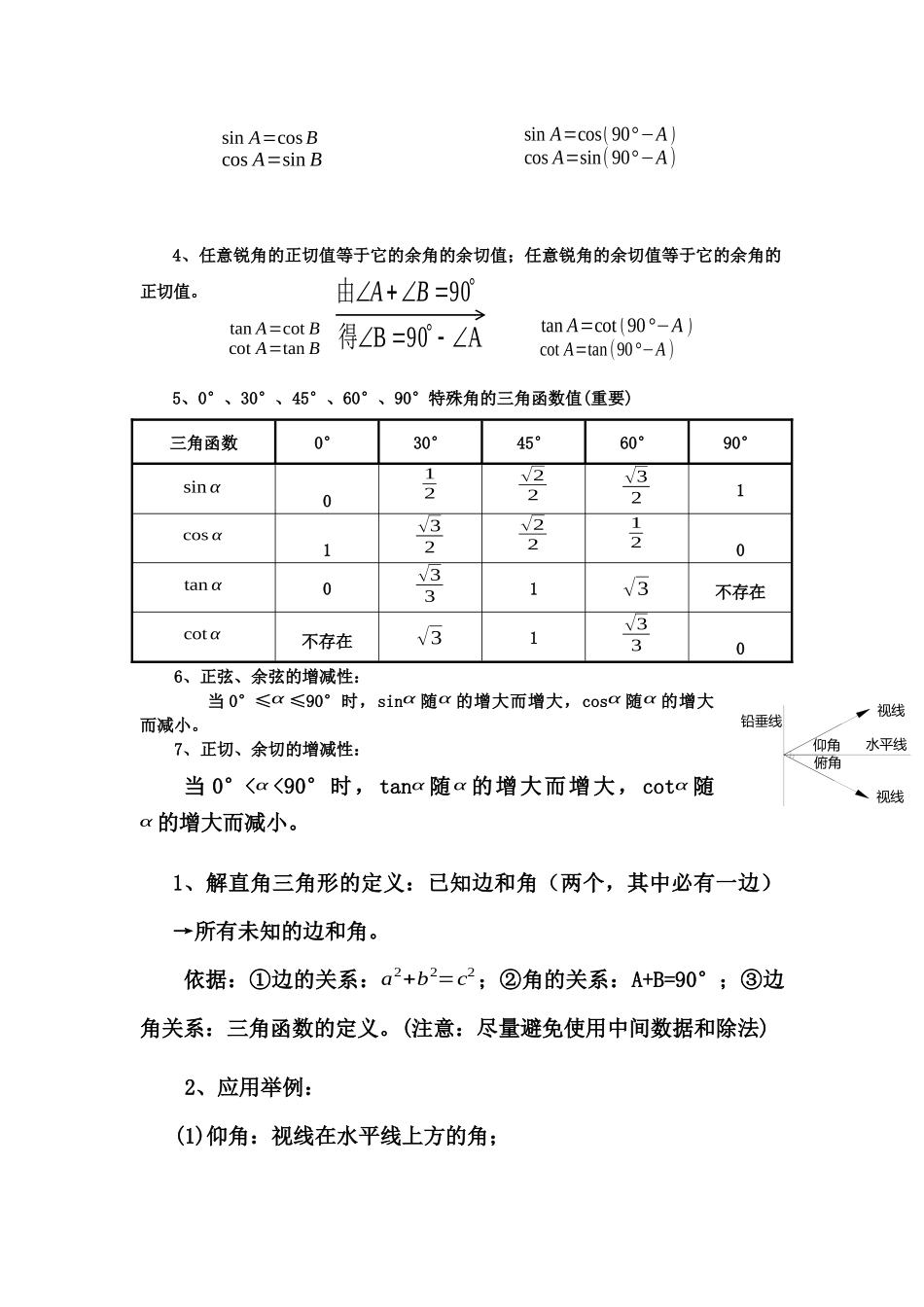
对边b斜边ACBacA90B90得由BA锐角三角函数知识点总结与复习1、勾股定理:直角三角形两直角边a、b的平方和等于斜边c的平方。a2+b2=c22、如下图,在Rt△ABC中,∠C为直角,则∠A的锐角三角函数为(∠A可换成∠B):3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。定义表达式取值范围关系正弦sinA=∠A的对边斜边sinA=ac00(∠A为锐角)tanA=cotBcotA=tanBtanA=1cotA(倒数)tanA⋅cotA=1余切cotA=∠A的邻边∠A的对边cotA=bacotA>0(∠A为锐角)A90B90得由BA4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值。5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)三角函数0°30°45°60°90°sinα012√22√321cosα1√32√22120tanα0√331√3不存在cotα不存在√31√3306、正弦、余弦的增减性:当0°≤α≤90°时,sinα随α的增大而增大,cosα随α的增大而减小。7、正切、余切的增减性:当0°<α<90°时,tanα随α的增大而增大,cotα随α的增大而减小。1、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。依据:①边的关系:a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义。(注意:尽量避免使用中间数据和除法)2、应用举例:(1)仰角:视线在水平线上方的角;仰角铅垂线水平线视线视线俯角sinA=cosBcosA=sinBsinA=cos(90°−A)cosA=sin(90°−A)tanA=cotBcotA=tanBtanA=cot(90°−A)cotA=tan(90°−A):ihlhlα(2)俯角:视线在水平线下方的角。(3)坡面的铅直高度和水平宽度的比叫做坡度(坡比)。用字母表示,即。坡度一般写成的形式,如等。把坡面与水平面的夹角记作(叫做坡角),那么。3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。如图3,OA、OB、OC、OD的方向角分别是:45°、135°、225°。4、指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角。如图4:OA、OB、OC、OD的方向角分别是:北偏东30°(东北方向),南偏东45°(东南方向),南偏西60°(西南方向),北偏西60°(西北方向)。锐角三角函数(1)基础扫描1.求出下图中sinD,sinE的值.85FEDlPCBA(第6题图)CBA(第7题图)2.把Rt△ABC各边的长度都扩大2倍得Rt△A′B′C′,那么锐角A、A′的正弦值的关系为().A.sinA=sinA′B.sinA=2sinA′C.2sinA=sinA′D.不能确定3.在Rt△ABC中,∠C=90°,若AB=5,AC=4,则sinB的值是()A.B.C.D.4.如图,△ABC中,AB=25,BC=7,CA=24.求sinA的值.5.计算:sin30°·sin60°+sin45°.能力拓展6.如图,B是线段AC的中点,过点C的直线l与AC成60°的角,在直线上取一点P,连接AP、PB,使sin∠APB=,则满足条件的点P的个数是()A1个B2个C3个D不存在7.如图,△ABC中,∠A是锐角,求证:8.等腰△ABC中,AB=AC=5,BC=6,求sinA、sinB.创新学习9.如图,△ABC的顶点都是正方形网格中的格点,则sin∠BAC等于()A.B.C.D.锐角三角函数(2)基础扫描1.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,若b=3a,则tanA=.2.在△ABC中,∠C=90°,cosA=,c=4,则a=_______.3.如果是等腰直角三角形的一个锐角,则的值是()25247CBAbaEDCBA(第8题图)A.B.C.D.4.如图,P是∠α的边OA上一点,且P点坐标为(2,3),则sinα=_______,cosα=_________,tanα=______.5.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若,,则tan∠ACD的值为()A.B.C.D.6.已知α是锐角,且cosα=,求sinα、tanα的值.能力拓展7.若α为锐角,试证明:.8.如图,在Rt△ABC中,CD、CE分别为斜边AB上的高和中线,BC=a,AC=b(b>a),若tan∠DCE=,求的值.创新学习9.如图,Rt△ABC中,∠C=90°,D为CA上一点,∠DBC=30°,DA=3,AB=,试求cosA与tanA的值.锐角三角函数(3)CBADyxP(2,3)OA基础扫描1.已知sinα...