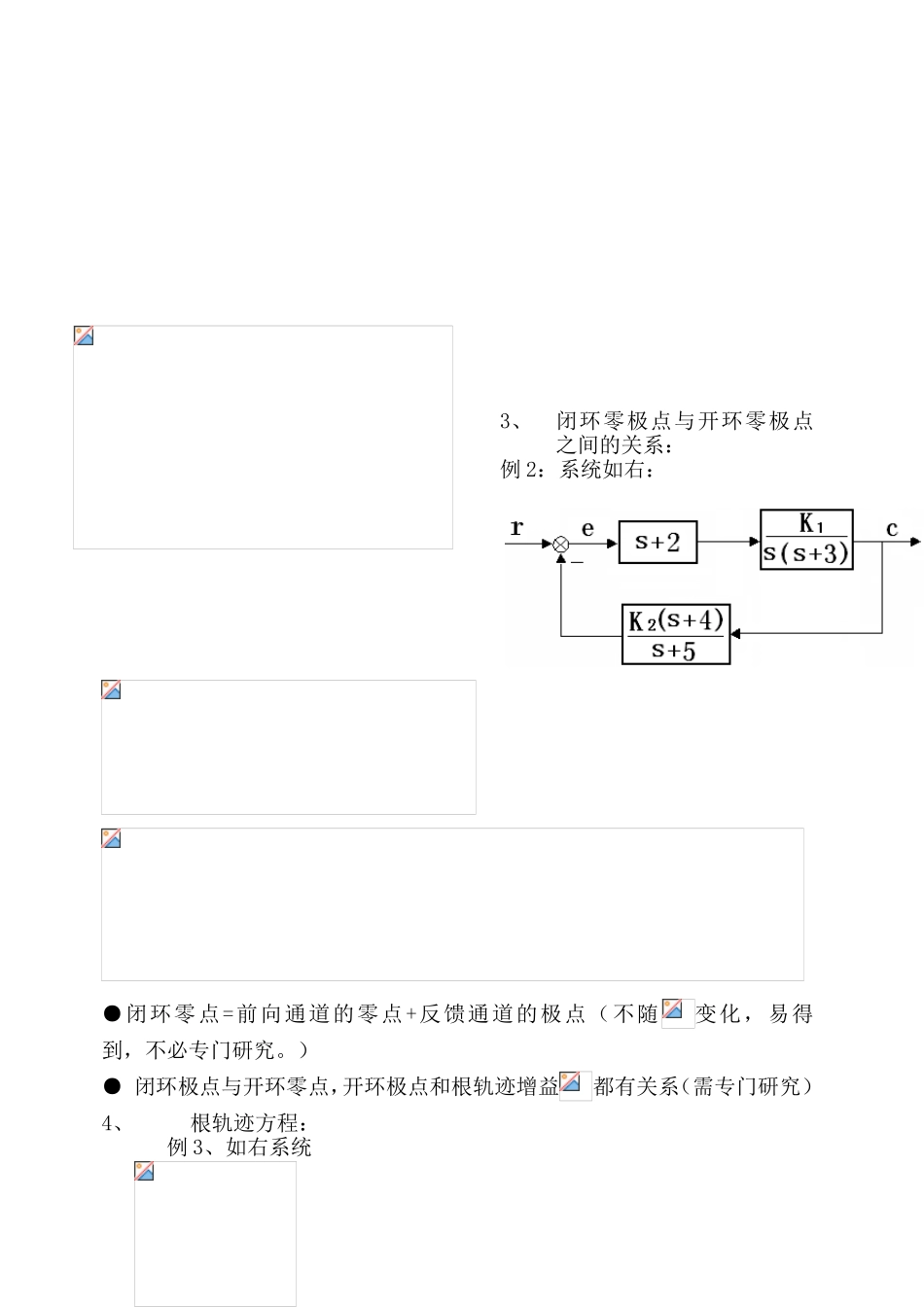
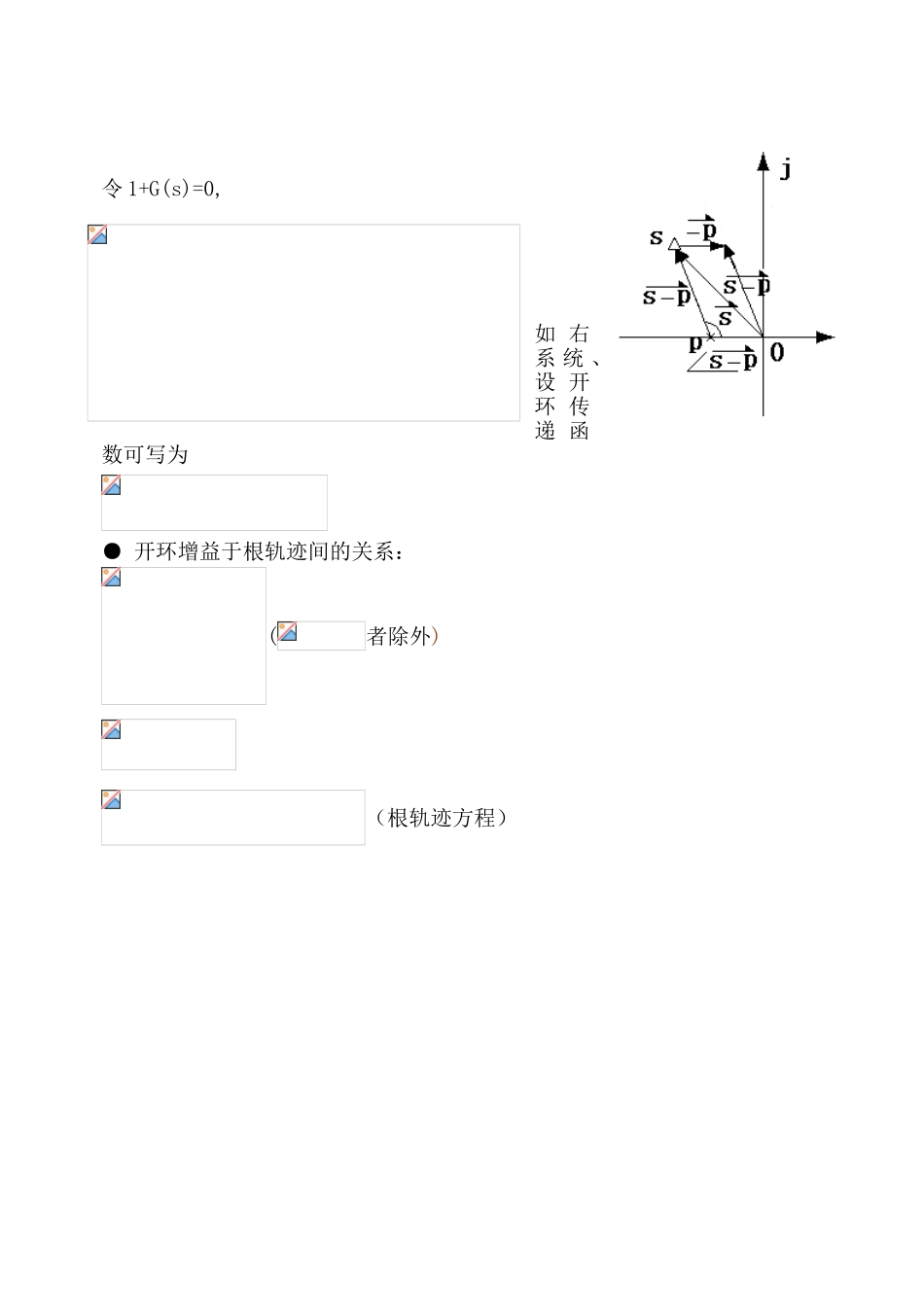
第四章线性系统的根轨迹法闭环系统的性能由闭环零极点分布决定。当开环传递函数中某个参数变化时,闭环系统特征方程的系数也相应变化,闭环极点也要改变(解根难)。研究闭环极点随开环某参数变化而变化的规律,进而讨论闭环系统性能的变化趋势,是具有理论和实际工程意义的课题。(调参、设计等)。根轨迹的特点:●图解法,简单;●特别适用于研究当系统的开环参数变化时,系统性能的变化趋势问题;●近似方法,不十分精确。§4.1根轨迹的基本概念1、根轨迹的概念:当开环系统某一参数从0到∞变化时,闭环极点在S平面上变化所描绘出的轨迹。例1:系统如右:根轨迹增益。闭环传递函数为:闭环特征方程为:特征根为:,当系统参数(或)从零变化到无穷时,闭环极点的变化情况如表4-1所示。表4-1、=0~时系统的特征根000-20.50.25-0.3-1.710.5-1-121-1+j-1-j52.5-1+j2-1-j2∞∞-1+j∞-1-j∞3、闭环零极点与开环零极点之间的关系:例2:系统如右:●闭环零点=前向通道的零点+反馈通道的极点(不随变化,易得到,不必专门研究。)●闭环极点与开环零点,开环极点和根轨迹增益都有关系(需专门研究)4、根轨迹方程:例3、如右系统令1+G(s)=0,如右系统、设开环传递函数可写为●开环增益于根轨迹间的关系:(者除外)(根轨迹方程)例4、系统开环极点分布如右图所示,分别讨论是否在根轨迹上。●任一点S,总可以有一个与之对应,满足模值条件,但它不一定在根轨迹上(不一定满足相角条件)。●满足相角条件的S,也一定有对应的使之满足模值条件,所以相角条件是判定S在不在根轨迹上的充要条件。●当S满足相角条件时,它一定在根轨迹上,所对应的值,由模值条件确定。§4.2绘制根轨迹的基本法则1、起点和终点:根轨迹起始于开环极点,终止于开环零点;如果开环零点个数少于开环极点个数,则有条根轨迹终止于无穷远处。起点:终点:2、根轨迹的分支数及对称性:3、实轴上的根轨迹:从实轴最右端的开环零极点算起,奇数开环零极点到偶数开环零极点间一定是根轨迹,否则一定不是证明:见右图为例说明∴S是根轨迹上的点。●定理:当开环极点有2个,开环零点有1个,并且在复平面上有根轨迹时,则复平面上的根轨迹一定是以零点为圆心的圆弧。证明:(见下面两页)要求:对于二阶系统的根轨迹,一定要能画的熟练准确。例:例:单位反馈系统其开环传递函数为,画出当时系统闭环根轨迹,证明根轨迹是圆,求出圆心和半径。解:(实轴上的根轨迹:根位于复平面时,有)分离点处,有解出:性能分析:快:稳:全过程稳定准:4、根之和,闭环根之和保持一个常数证明:即:●,在s平面上有一部分极点随变化向左移,则另一部分必然向右移,移动的总增量为0,保证根之和为常数。如右根轨迹:25、渐近线:n-m个极点趋于无穷远点的规律。“广义重心”如右根轨迹:将闭环极点、闭环零点(不一定是开环零点)标在[s]平面上,便可以计算闭环性能。△注:1)、根轨迹法研究的是当系统参数变化时,闭环极点的变化规律。2)、根轨迹法的目的:在于通过研究参数变化、根变化的规律,来研究闭环系统性能的变化规律。例1、系统结构图如右:Ⅰ、作时的根轨迹。解:1、起点、终点2、分支数、对称性3、实轴上的根轨迹4、根之和5、渐近线:用根之和解释为什么根轨迹是这样6、分离点坐标d分离点d的一般公式:即有:试根:(1)、现在根轨迹上判断一下d的大致范围:-0.5~-1之间。(2)、先取=-0.5;上面方程不平衡。再取=-0.6;上面方程反相不平衡(选择方向对,但过头了)选=-0.55;方程基本平衡()(3)、d的精度到以内即可。II、分析当变化过程中,闭环系统动态性能的变化规律。系统始终稳定。III、确定两复数闭环极点实部为-1时,标出闭环极点、零点,定性分析其性能。系统动态性能主要取决于一对共轭复极点实际响应对应的应比只有时要小(比之更靠近原点)。具体指标的数值可以用P160相应公式计算。求一对复根实部为-1时对应的根轨迹增益及三个根的坐标。解法一、①先由根之和法则解出单根②由模值条件求出相应的③由长除法解出、坐标:依题意,应有:解出:∴商为:解出:解法二:依题意有:左边展开式右边展开式比较系数有:联...