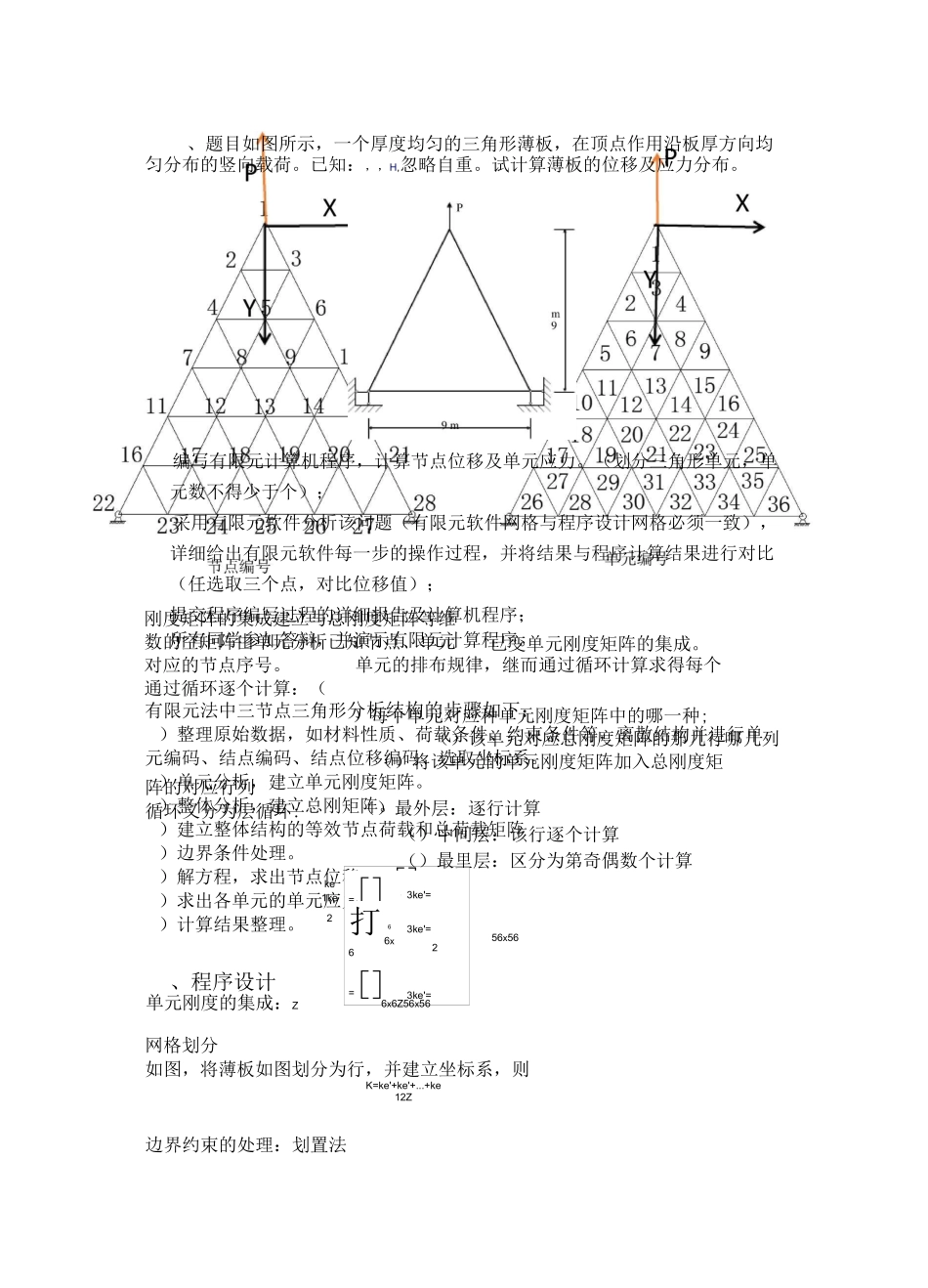
、题目如图所示,一个厚度均匀的三角形薄板,在顶点作用沿板厚方向均匀分布的竖向载荷。已知:,,H,忽略自重。试计算薄板的位移及应力分布。编写有限元计算机程序,计算节点位移及单元应力。(划分三角形单元,单元数不得少于个);采用有限元软件分析该问题(有限元软件网格与程序设计网格必须一致),详细给出有限元软件每一步的操作过程,并将结果与程序计算结果进行对比(任选取三个点,对比位移值);提交程序编写过程的详细报告及计算机程序;所有同学参加答辩,并演示有限元计算程序。有限元法中三节点三角形分析结构的步骤如下:)整理原始数据,如材料性质、荷载条件、约束条件等,离散结构并进行单元编码、结点编码、结点位移编码、选取坐标系。)单元分析,建立单元刚度矩阵。)整体分析,建立总刚矩阵。)建立整体结构的等效节点荷载和总荷载矩阵)边界条件处理。)解方程,求出节点位移。)求出各单元的单元应力。)计算结果整理。、程序设计网格划分如图,将薄板如图划分为行,并建立坐标系,则刚度矩阵的集成建立与总刚度矩阵等维数的空矩阵由单元分析已知节点、单元对应的节点序号。通过循环逐个计算:(已变单元刚度矩阵的集成。单元的排布规律,继而通过循环计算求得每个)每个单元对应种单元刚度矩阵中的哪一种;()该单元对应总刚度矩阵的那几行哪几列()将该单元的单元刚度矩阵加入总刚度矩阵的对应行列循环又分为层循环:()最外层:逐行计算()中间层:该行逐个计算()最里层:区分为第奇偶数个计算一[]单元刚度的集成:Z=[]3ke'=打63ke'=6x62=[]3ke'=56x56ke1ke26x6Z56x56K=ke'+ke'+...+ke12Z边界约束的处理:划置法适用:这种方法适用于边界节点位移分量为已知含为的各种约束。做法:()将总刚矩阵〔〕中相应于已知位移行主对角线元素置,其他元素改为零;同时将载荷列阵{}中相应元素用已知位移置换。◎这样,由该方程求得的此位移值一定等于已知量。()将〔〕中已知位移相应的列的非主对角成元素也置,以保持〔〕的对称性。◎当然,在已知位移分量不为零的情况下,这样做就改变了方程左端的数值,为保证方程成立,须在方程右端减去已知位移对该方程的贡献——已知位移和相应总刚元素的乘积。◎若约束为零位移约束时,此步则可省去。特点:()经以上处理同样可以消除刚性位移约束足够的前提下,去掉未知约束反力。()但这种方法不改变方程阶数,利于存贮。()不过,若是要求出约束反力,仍要重新计算各个划去的总刚元素...