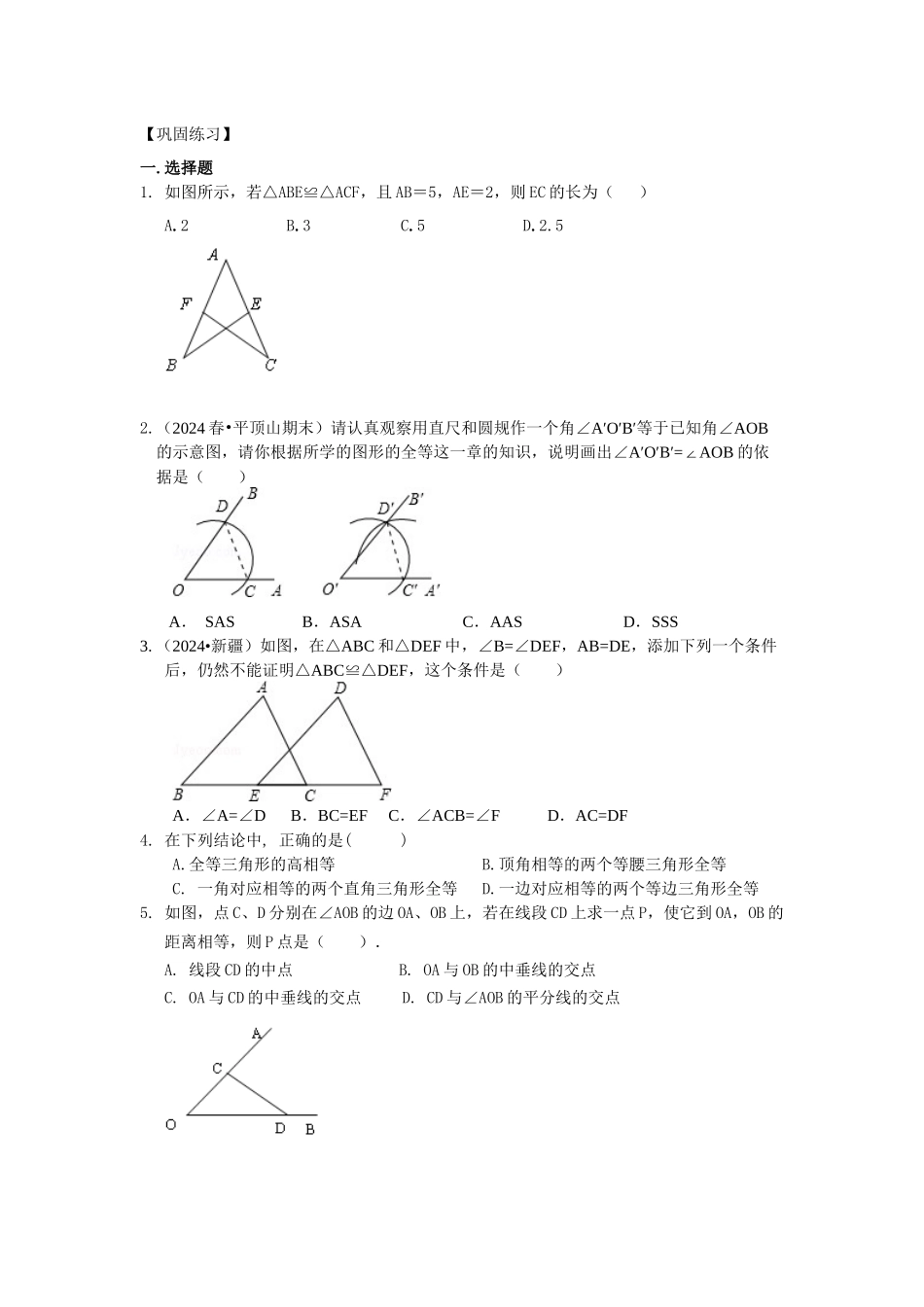
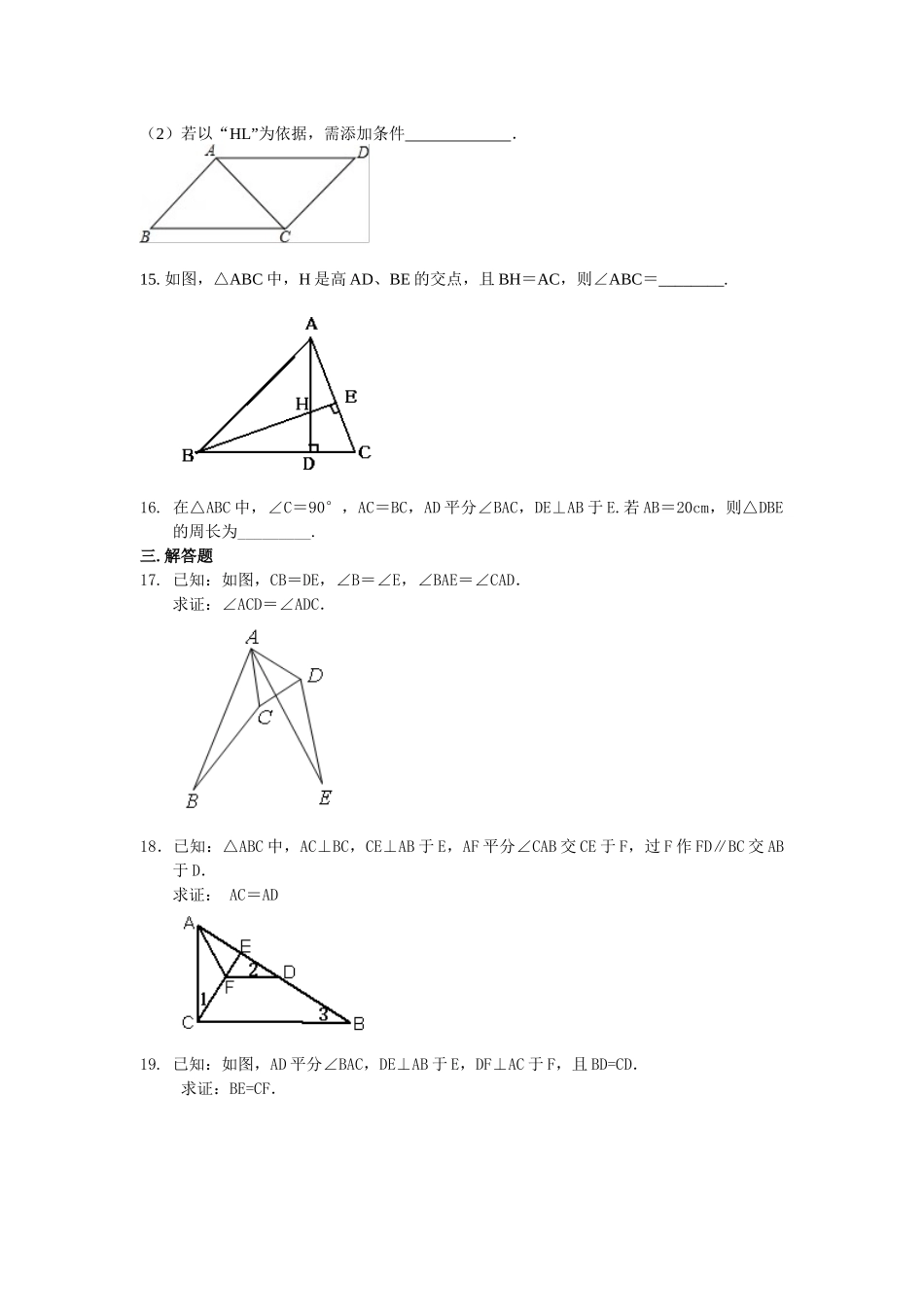
【巩固练习】一.选择题1. 如图所示,若△ABE≌△ACF,且 AB=5,AE=2,则 EC 的长为( )A.2 B.3 C.5 D.2.52.(2024 春•平顶山期末)请认真观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,请你根据所学的图形的全等这一章的知识,说明画出∠A′O′B′=AOB∠的依据是( ) A. SASB.ASAC.AASD.SSS3. (2024•新疆)如图,在△ABC 和△DEF 中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )A.∠A=∠D B.BC=EF C.∠ACB=∠F D.AC=DF4. 在下列结论中, 正确的是( ) A.全等三角形的高相等B.顶角相等的两个等腰三角形全等 C. 一角对应相等的两个直角三角形全等D.一边对应相等的两个等边三角形全等5. 如图,点 C、D 分别在∠AOB 的边 OA、OB 上,若在线段 CD 上求一点 P,使它到 OA,OB 的距离相等,则 P 点是( ). A. 线段 CD 的中点 B. OA 与 OB 的中垂线的交点 C. OA 与 CD 的中垂线的交点 D. CD 与∠AOB 的平分线的交点6.在△ABC 与△DEF 中,给出下列四组条件:(1)AB=DE,BC=EF,AC=DF;(2)AB=DE,∠B=∠E,BC=EF;(3)∠B=∠E,BC=EF,∠C=∠F;(4)AB=DE,AC=DF,∠B=∠E.其中,能使△ABC≌△DEF 的条件共有( )组.A.1 组 B.2 组 C.3 组 D.4 组7. 假如两个锐角三角形有两条边和其中一边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是( )A. 相等 B.不相等 C.互补 D.相等或互补8. △ABC 中,∠BAC=90° AD⊥BC,AE 平分∠BAC,∠B=2∠C,∠DAE 的度数是( ) A.45° B.20° C.、30° D.15°二.填空题9. 已知,若△ABC 的面积为 10 ,则的面积为________ ,若的周长为 16,则△ABC 的周长为________.10. △ABC 和△ADC 中,下列三个论断:① AB=AD;②∠BAC=∠DAC;③ BC=DC.将两个论断作为条件,另一个论断作为结论构成一个命题,写出一个真命题:__________.11.(2024 春•成都校级期末)如图,在△ABC 中,∠C=90°,∠B=30°,AD 平分∠BAC,CD=2cm,则 BD 的长是 .12. 下列说法中:①假如两个三角形可以依据“AAS”来判定全等,那么一定也可以依据“ASA”来判定它们全等;②假如两个三角形都和第三个三角形不全等,那么这两个三角形也一定不全等;③要推断两个三角形全等,给出的条件中至少要有一对边对应相等.正确的...