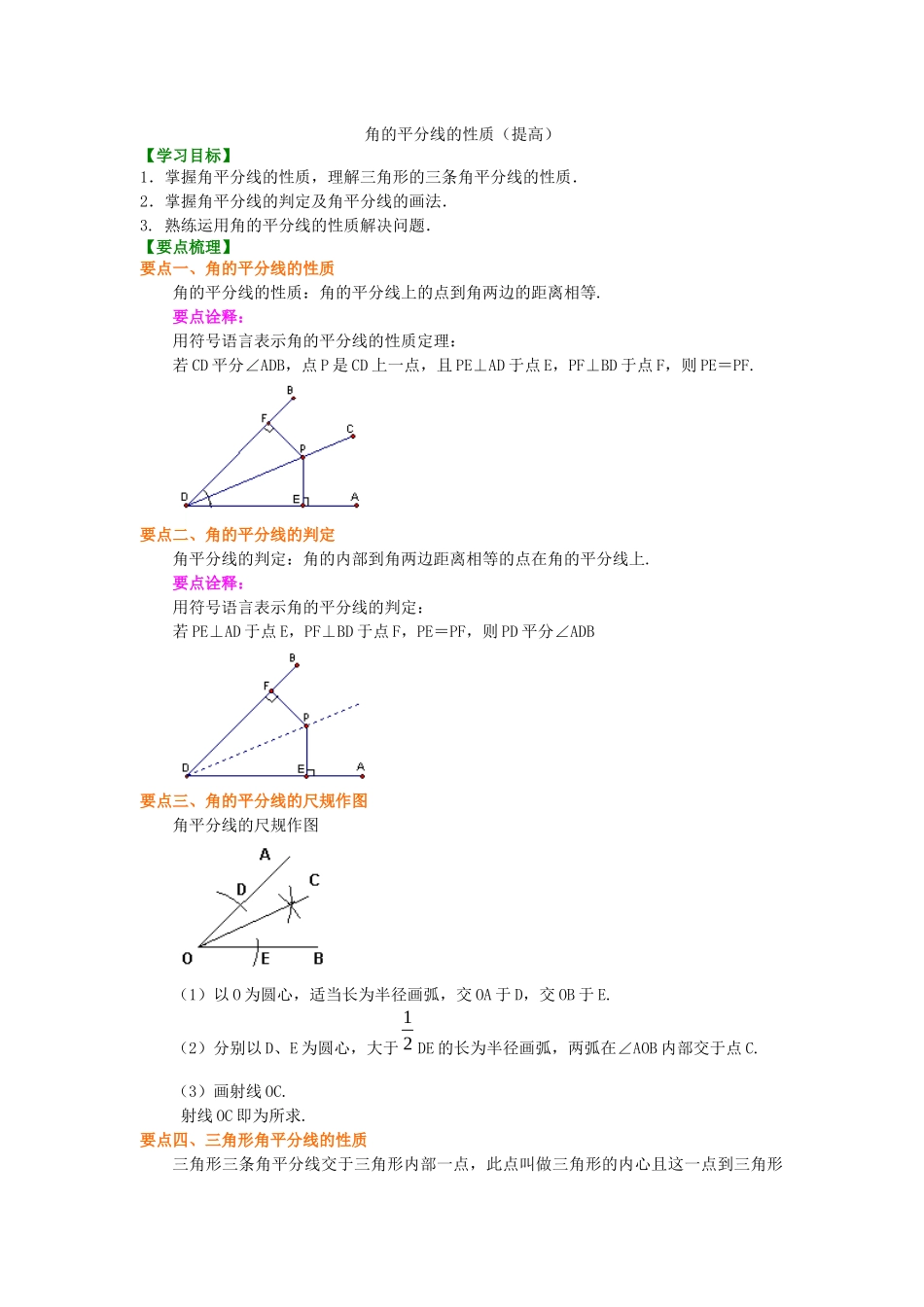
角的平分线的性质(提高)【学习目标】1.掌握角平分线的性质,理解三角形的三条角平分线的性质.2.掌握角平分线的判定及角平分线的画法.3. 熟练运用角的平分线的性质解决问题.【要点梳理】要点一、角的平分线的性质 角的平分线的性质:角的平分线上的点到角两边的距离相等.要点诠释:用符号语言表示角的平分线的性质定理:若 CD 平分∠ADB,点 P 是 CD 上一点,且 PE⊥AD 于点 E,PF⊥BD 于点 F,则 PE=PF.要点二、角的平分线的判定 角平分线的判定:角的内部到角两边距离相等的点在角的平分线上.要点诠释:用符号语言表示角的平分线的判定:若 PE⊥AD 于点 E,PF⊥BD 于点 F,PE=PF,则 PD 平分∠ADB要点三、角的平分线的尺规作图角平分线的尺规作图(1)以 O 为圆心,适当长为半径画弧,交 OA 于 D,交 OB 于 E. (2)分别以 D、E 为圆心,大于DE 的长为半径画弧,两弧在∠AOB 内部交于点 C. (3)画射线 OC.射线 OC 即为所求.要点四、三角形角平分线的性质三角形三条角平分线交于三角形内部一点,此点叫做三角形的内心且这一点到三角形12三边的距离相等.三角形的一内角平分线和另外两顶点处的外角平分线交于一点.这点叫做三角形的旁心.三角形有三个旁心.所以到三角形三边所在直线距离相等的点共有 4 个.如图所示:△ABC的内心为,旁心为,这四个点到△ABC 三边所在直线距离相等.【典型例题】类型一、角的平分线的性质及判定1、(2024 秋•新洲区期末)如图,在△ABC 中,∠ABC 的平分线与∠ACB 的外角的平分线相交于点 P,连接 AP.(1)求证:PA 平分∠BAC 的外角∠CAM;(2)过点 C 作 CE⊥AP,E 是垂足,并延长 CE 交 BM 于点 D.求证:CE=ED.【思路点拨】(1)过 P 作 PT⊥BC 于 T,PS⊥AC 于 S,PQ⊥BA 于 Q,根据角平分线性质求出PQ=PS=PT,根据角平分线性质得出即可;(2)根据 ASA 求出△AED≌△AEC 即可.【答案与解析】证明:(1)过 P 作 PT⊥BC 于 T,PS⊥AC 于 S,PQ⊥BA 于 Q,如图, 在△ABC 中,∠ABC 的平分线与∠ACB 的外角的平分线相交于点 P,∴PQ=PT,PS=PT,∴PQ=PS,∴AP 平分∠DAC,即 PA 平分∠BAC 的外角∠CAM;1P234,,P P P(2) PA 平分∠BAC 的外角∠CAM,∴∠DAE=∠CAE, CE⊥AP,∴∠AED=∠AEC=90°,在△AED 和△AEC 中∴△AED≌△AEC,∴CE=ED.【总结升华】本题考查了角平分线性质和全等三角形的...