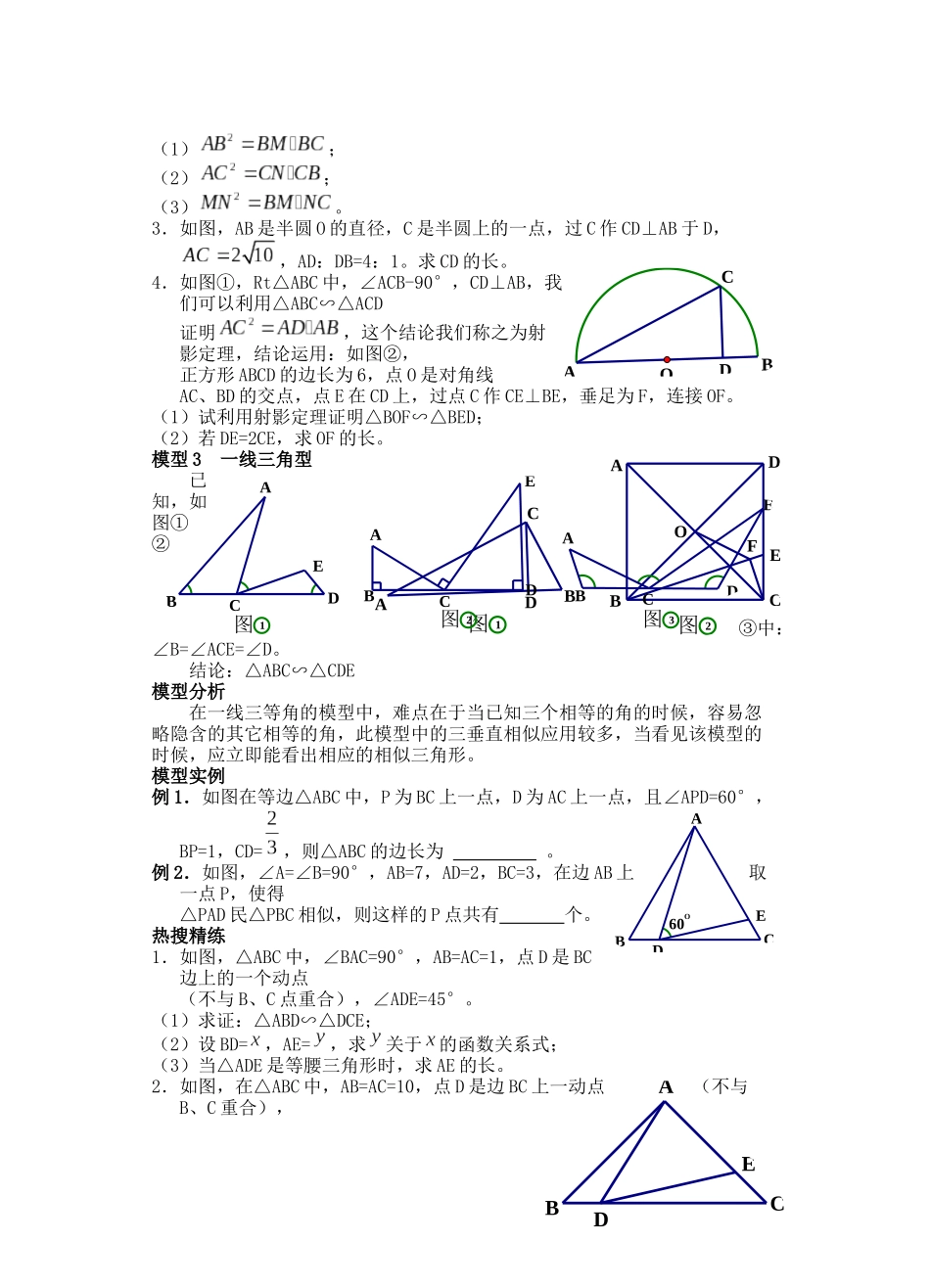
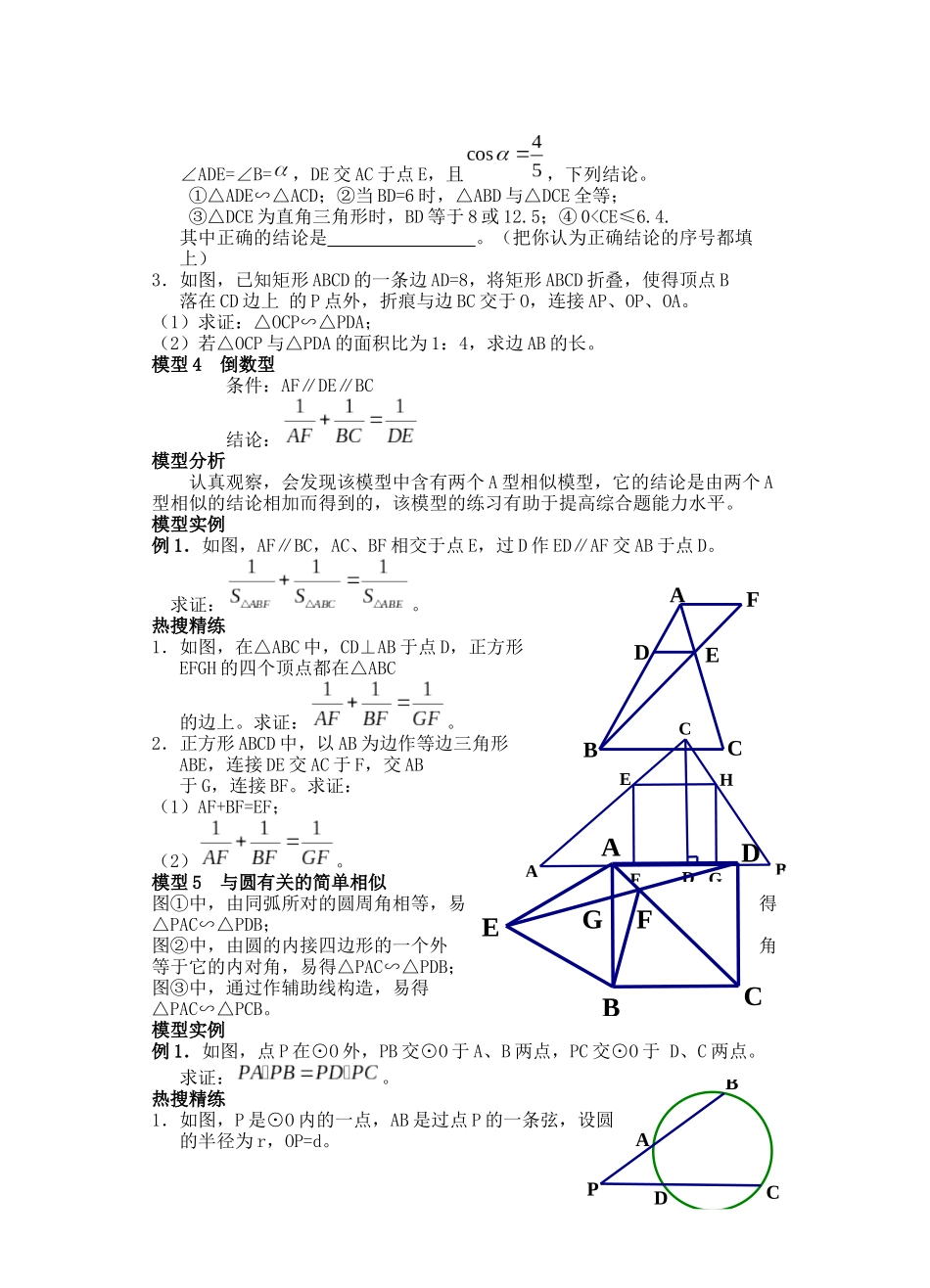
第十章 相似模型 求证:。例 2.如图,点 E、F 分别在菱形 ABCD 的边 AB、AD 上,且 AE=DF,BF 交 DE 于 点 G,延长 BF 交 CD 的延长线于 H,若。求的值。热搜精练1.如图,D、E 分别是△ABC 的边 AB、BC上的点,且 DE∥AC,AE、CD 相交 于点 O,若 S△DOE:S△COA=1:25,则 S△BDE与 S△CDEE的比是 。2.如图所示,□ABCD 中,G 是 BC 延长线上的一点,AG 与 BD 交于点 E,与 DC 交于点 F,此图中的相似三角形共有 对。3.如图,在△ABC 中,中线 BD、CE 相交于点 O,连接 AO 并延长,交 BC 于点 F。求证:点 F 是 BC 的中点。4.在△ABC 中,AD 是角平分线,求证:。5.如图,△ABC 为等腰直角三角形,∠ACB-90°,D 是边BC 的中点,E 在 AB 上,且 AE:BE=2:1。求证:CE⊥AD。模型 2 共边共角型 已知:∠1=∠2 结论:△ACD∽△ABC模型分析上图中,不仅要熟悉模型,还要熟记模型的结论,有时候题目中会给出三角形边的乘积或比例关系,我们要能快速推断题中的相似三角形,模型中由△ACD∽△ABC,进而可以得到。模型实例例 1.如图,D 是△ABC 边 BC 上的一点,AB=4, AD=2,∠DAC=∠B,假如△ABD 的面积为 15, 那么△ACD 的面积为 。例 2.如图,在 Rt△ABC 中,∠BAC-90°,AD⊥BC 于D。(1)图中有多少对相似三角形?写出来;(2)求证:热搜精练1.如图所示,能判定△ABC∽△DAC 的有 ; ①∠B=∠DAC;②∠BAC=∠ADC;③;④。2.已知△AMN 是等边三角形,∠BAC=120°。求证:ADBECOADBECFOADBCADBECDBCADBCADBCABCAMN(1);(2);(3)。3.如图,AB 是半圆 O 的直径,C 是半圆上的一点,过 C 作 CD⊥AB 于 D, ,AD:DB=4:1。求 CD 的长。4.如图①,Rt△ABC 中,∠ACB-90°,CD⊥AB,我们可以利用△ABC∽△ACD 证明,这个结论我们称之为射影定理,结论运用:如图②, 正方形 ABCD 的边长为 6,点 O 是对角线AC、BD 的交点,点 E 在 CD 上,过点 C 作 CE⊥BE,垂足为 F,连接 OF。(1)试利用射影定理证明△BOF∽△BED;(2)若 DE=2CE,求 OF 的长。模型 3 一线三角型 已知,如图①②③中:∠B=∠ACE=∠D。 结论:△ABC∽△CDE模型分析在一线三等角的模型中,难点在于当已知三个相等的角的时候,容易忽略隐含的其它相等的角,此模型中的三垂直相似应用较多,当看见该模型的时候,应立即能看出相应的...