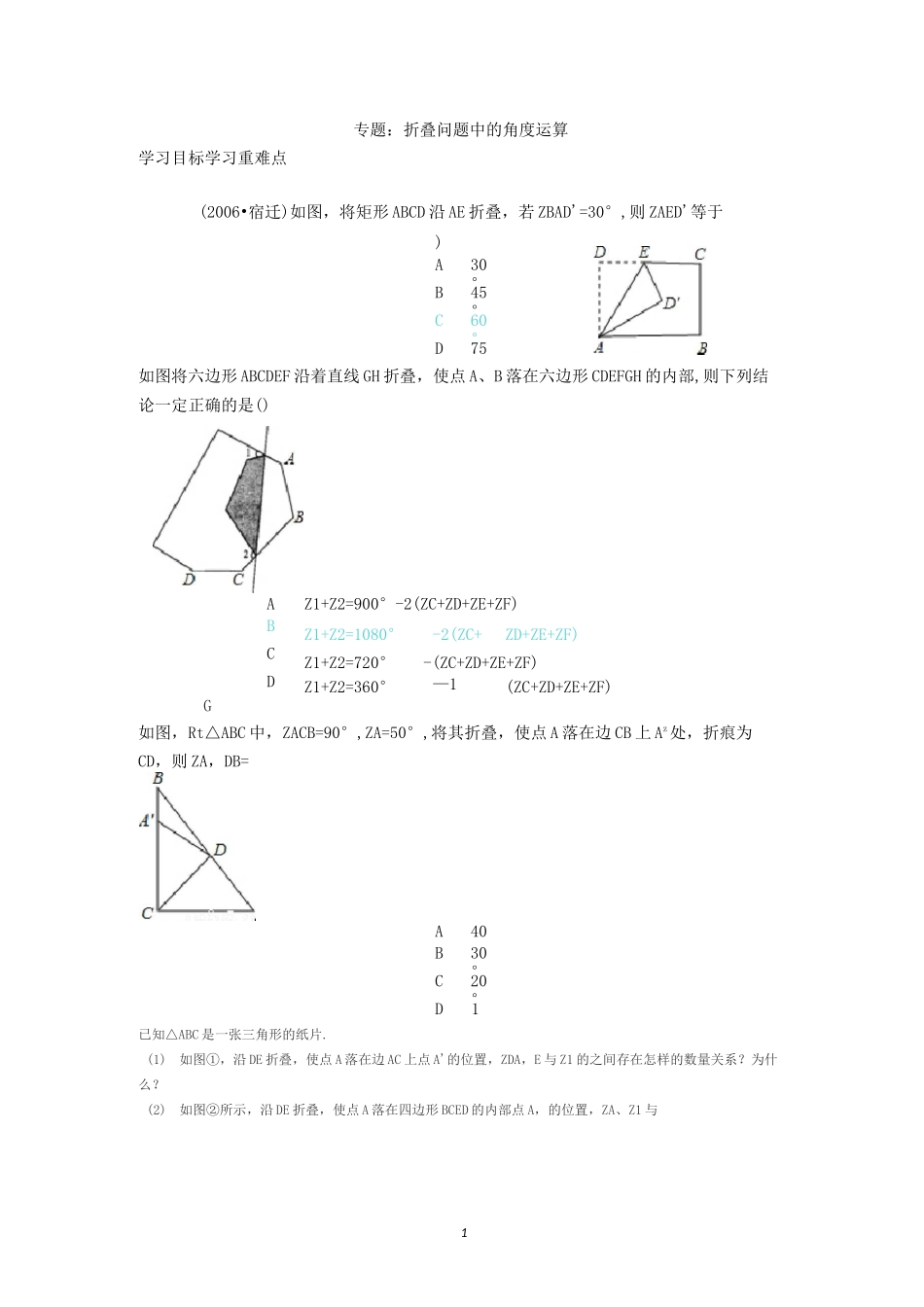
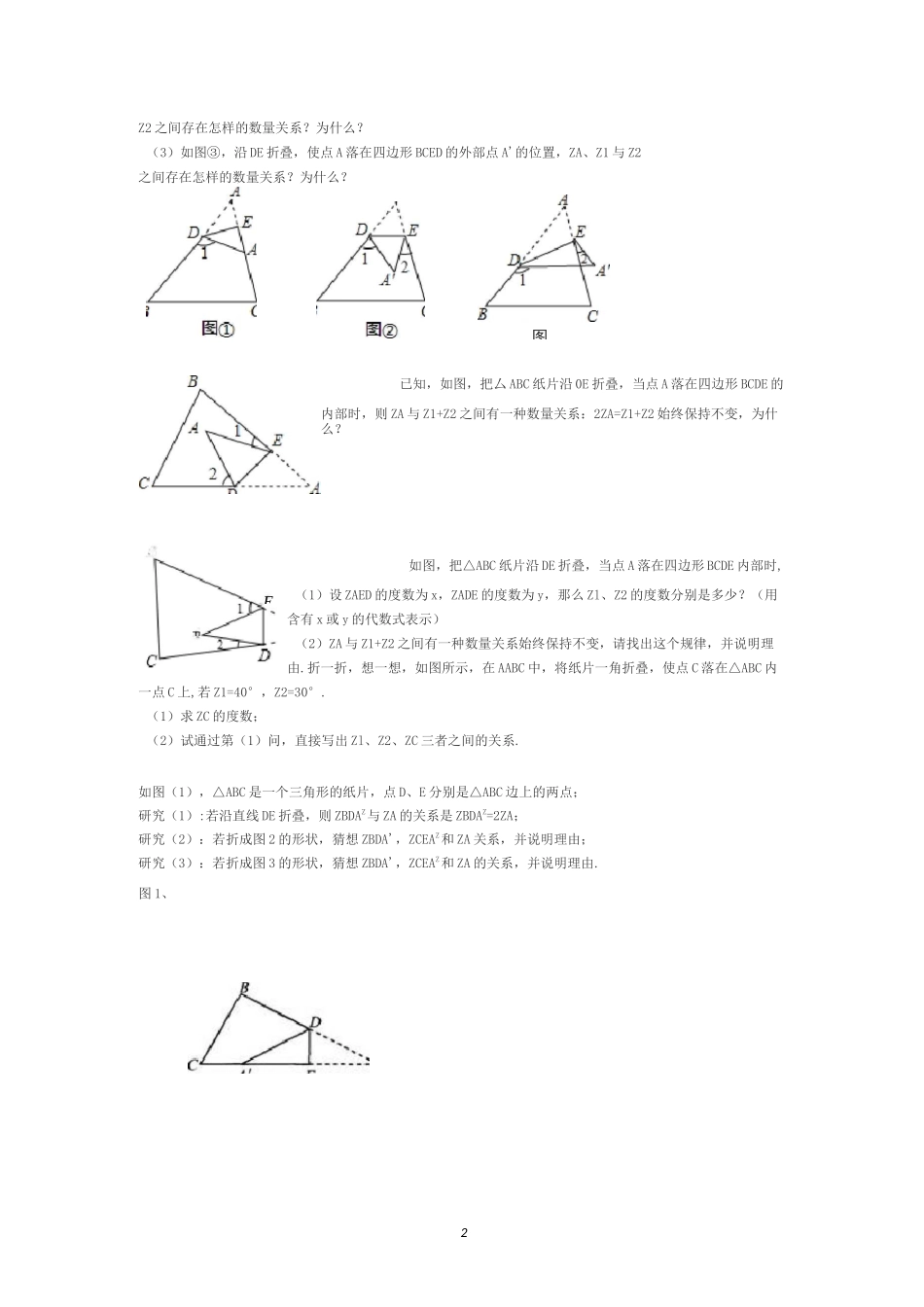
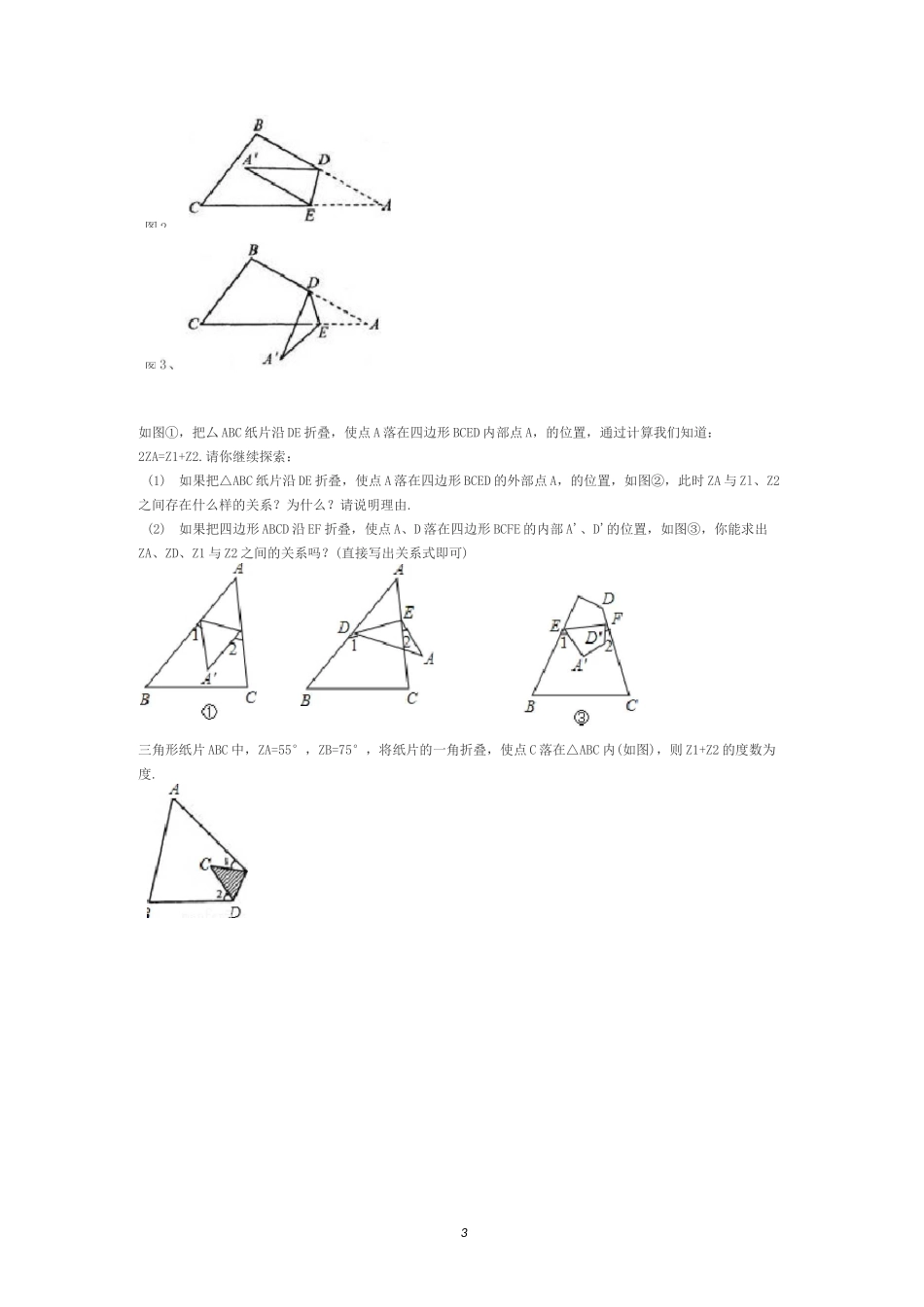
1专题:折叠问题中的角度运算学习目标学习重难点(2006•宿迁)如图,将矩形 ABCD 沿 AE 折叠,若 ZBAD'=30°,则 ZAED'等于)A.30°B.45°C.60°D.75°如图将六边形 ABCDEF 沿着直线 GH 折叠,使点 A、B 落在六边形 CDEFGH 的内部,则下列结论一定正确的是()A.Z1+Z2=900°-2(ZC+ZD+ZE+ZF)B.Z1+Z2=1080°-2(ZC+ZD+ZE+ZF)C.Z1+Z2=720°-(ZC+ZD+ZE+ZF)D.Z1+Z2=360°—1(ZC+ZD+ZE+ZF)G如图,Rt△ABC 中,ZACB=90°,ZA=50°,将其折叠,使点 A 落在边 CB 上 Az处,折痕为CD,则 ZA,DB=A.40°B.30°C.20°D.10°已知△ABC 是一张三角形的纸片.(1)如图①,沿 DE 折叠,使点 A 落在边 AC 上点 A'的位置,ZDA,E 与 Z1 的之间存在怎样的数量关系?为什么?(2)如图②所示,沿 DE 折叠,使点 A 落在四边形 BCED 的内部点 A,的位置,ZA、Z1 与2图Z2 之间存在怎样的数量关系?为什么?(3)如图③,沿 DE 折叠,使点 A 落在四边形 BCED 的外部点 A'的位置,ZA、Z1 与 Z2之间存在怎样的数量关系?为什么?已知,如图,把厶 ABC 纸片沿 0E 折叠,当点 A 落在四边形 BCDE 的内部时,则 ZA 与 Z1+Z2 之间有一种数量关系:2ZA=Z1+Z2 始终保持不变,为什么?如图,把△ABC 纸片沿 DE 折叠,当点 A 落在四边形 BCDE 内部时,(1)设 ZAED 的度数为 x,ZADE 的度数为 y,那么 Zl、Z2 的度数分别是多少?(用含有 x 或 y 的代数式表示)(2)ZA 与 Z1+Z2 之间有一种数量关系始终保持不变,请找出这个规律,并说明理由.折一折,想一想,如图所示,在 AABC 中,将纸片一角折叠,使点 C 落在△ABC 内一点 C 上,若 Z1=40°,Z2=30°.(1)求 ZC 的度数;(2)试通过第(1)问,直接写出 Zl、Z2、ZC 三者之间的关系.如图(1),△ABC 是一个三角形的纸片,点 D、E 分别是△ABC 边上的两点;研究(1):若沿直线 DE 折叠,则 ZBDAZ与 ZA 的关系是 ZBDAZ=2ZA;研究(2):若折成图 2 的形状,猜想 ZBDA',ZCEAZ和 ZA 关系,并说明理由;研究(3):若折成图 3 的形状,猜想 ZBDA',ZCEAZ和 ZA 的关系,并说明理由.图 1、E卫图 2、3如图①,把厶 ABC 纸片沿 DE 折叠,使点 A 落在四边形 BCED 内部点 A,的位置,通过计算我们知道:2ZA=Z1+Z2.请你继续探索:(1)如果把△ABC 纸片沿 DE 折叠,使点 A 落在四边形 BCED 的外部点 A,的位置,如图...