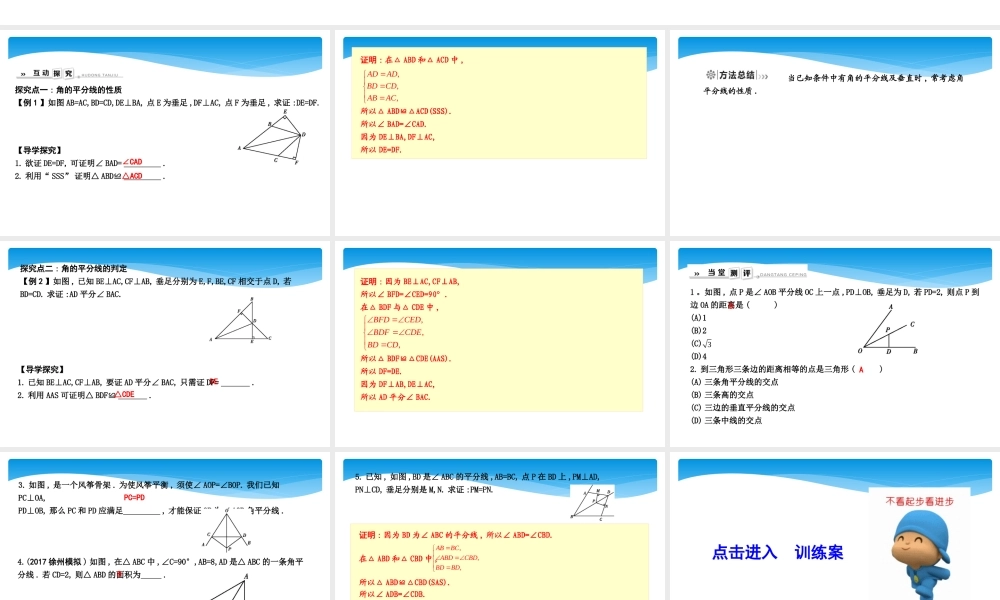
12.3 角的平分线的性质一、角的平分线的性质和判定1. 性质 : 角的平分线上的点到角的两边的 相等 . 2. 判定 : 角的内部到角的两边的 的点在角的平分线上 .二、证明几何命题的步骤1. 明确命题中的 和 . 2. 根据题意 , 画出图形 , 并用 表示已知和求证 . 3. 经过分析 , 找出由已知推出要证的结论的途径 , 写出 过程 . 距离距离相等已知求证符号证明探究点一 : 角的平分线的性质【例 1 】如图 AB=AC,BD=CD,DE⊥BA, 点 E 为垂足 ,DF⊥AC, 点 F 为垂足 , 求证 :DE=DF.【导学探究】1. 欲证 DE=DF, 可证明∠ BAD= . 2. 利用“ SSS” 证明△ ABD≌ . ∠CAD△ACD证明 : 在△ ABD 和△ ACD 中 ,所以△ ABD≌△ACD(SSS).所以∠ BAD=∠CAD.因为 DE⊥BA,DF⊥AC,所以 DE=DF.,,,ADADBDCDABAC 当已知条件中有角的平分线及垂直时 , 常考虑角平分线的性质 . 探究点二 : 角的平分线的判定【例 2 】如图 , 已知 BE⊥AC,CF⊥AB, 垂足分别为 E,F,BE,CF 相交于点 D, 若BD=CD. 求证 :AD 平分∠ BAC.DE【导学探究】1. 已知 BE⊥AC,CF⊥AB, 要证 AD 平分∠ BAC, 只需证 DF= . 2. 利用 AAS 可证明△ BDF≌ . △CDE证明 : 因为 BE⊥AC,CF⊥AB,所以∠ BFD=∠CED=90°.在△ BDF 与△ CDE 中 ,所以△ BDF≌△CDE(AAS).所以 DF=DE.因为 DF⊥AB,DE⊥AC,所以 AD 平分∠ BAC.,,,BFDCEDBDFCDEBDCD1 。如图 , 点 P 是∠ AOB 平分线 OC 上一点 ,PD⊥OB, 垂足为 D, 若 PD=2, 则点 P 到边 OA 的距离是 ( )(A)1(B)2(C) (D)42. 到三角形三条边的距离相等的点是三角形 ( )(A) 三条角平分线的交点(B) 三条高的交点(C) 三边的垂直平分线的交点(D) 三条中线的交点BA33. 如图 , 是一个风筝骨架 . 为使风筝平衡 , 须使∠ AOP=∠BOP. 我们已知PC⊥OA,PD⊥OB, 那么 PC 和 PD 应满足 , 才能保证 OP 为∠ AOB 角平分线 . PC=PD4.(2017 徐州模拟 ) 如图 , 在△ ABC 中 ,∠C=90°,AB=8,AD 是△ ABC 的一条角平分线 . 若 CD=2, 则△ ABD 的面积为 . 8证明 : 因为 BD 为∠ ABC 的平分线 , 所以∠ ABD=∠CBD.在△ ABD 和△ CBD 中 ,所以△ ABD≌△CBD(SAS).所以∠ ADB=∠CDB.所以 DP 平分∠ ADC.因为 PM⊥AD,PN⊥CD,所以 PM=PN.5. 已知 , 如图 ,BD 是∠ ABC 的平分线 ,AB=BC, 点 P 在 BD 上 ,PM⊥AD,PN⊥CD, 垂足分别是 M,N. 求证 :PM=PN.,,,ABBCABDCBDBDBD点击进入 训练案