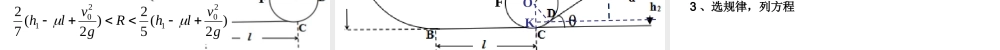能量观点解决力学问题F例 如图所示,在竖直平面内,曲线轨道 AB和圆轨道 CDEF 通过长为 l 的水平轨道 BC 平滑连接。质量为 m 的小球,从高 h1 的 A 点以 v0下滑,经过所有轨道时不脱离;不计一切阻力,重力加速度为 g ,求竖直圆轨道半径 R 的最大值RF)2(52201gvlhR变式 1 如图所示,在竖直平面内,曲线轨道 AB和圆轨道 CDEF 通过长为 l 的水平轨道 BC 平滑连接。质量为 m 的小球,从高 h1的 A 点以 v0下滑,经过所有轨道时不脱离;其中圆形轨道CDEF 能承受的最大压力为 8 倍重力,轨道 BC粗糙且动摩擦因数为 μ ,重力加速度为 g ,其它轨道摩擦阻力不计;求 R 的取值范围)2(52)2(72201201gvlhRgvlh变式 2 若 , m=1kg , h1=2m , l=2m ,R=0.5m ,水平轨道 MN 与地面高度差 h2=0.6m ;圆形轨道 CDEF 能承受的最大压力为 8 倍重力,倾角 θ=530的斜面 DM 与圆轨道相切于 D 点;斜面 DM 用长度可忽略的一小段光滑轨道与水平轨道 MN 平滑相连,轨道 BC 、斜面 DM 、水平轨道 MN 与小球的动摩擦因数 μ=0.4 ,其它摩擦阻力不计, g=10m/s2;要使小球最后能停止在MN 轨道上,求 MN 长度 d 的最小值smv/520 FOK3.7m小 结一、规律1 、动能定理: W 合=Ek2-Ek12 、机械能守恒定律: Ek2+Ep2=Ek1+Ep1二、步骤1 、定对象,选过程2 、析受力,求做功(判守恒)3 、选规律,列方程