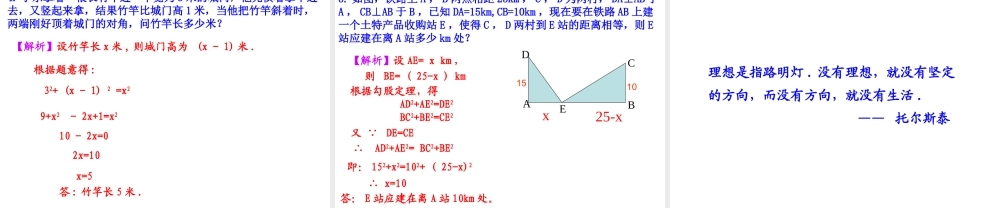
17.1 勾股定理第 2 课时1. 已知直角三角形的两条直角边分别为 a,b ,斜边为 c. 则a2= ( )b2= ( )c2= ( ) c2-b2c2-a2a2+b22. 在长方形 ABCD 中,宽 AB 为 1 m ,长 BC 为 2 m ,求 AC长.1 m2 mACBD 2222125 mACABBC在 Rt△ ABC 中,∠ B=90°, 由勾股定理可知:【解析】1. 熟练应用勾股定理解决直角三角形中的线段长度问题 .2. 能利用勾股定理解决实际问题 .一个门框尺寸如图所示.① 若有一块长 3 米,宽 0.8 米的薄木板,问怎样从门框通过?② 若薄木板长 3 米,宽 1.5 米呢?③ 若薄木板长 3 米,宽 2.2 米呢?为什么?ABC1 m2 m 木板的宽 2.2 米大于 1 米,∴ 横着不能从门框通过; 木板的宽 2.2 米大于 2 米,∴ 竖着也不能从门框通过.∴ 只能试试斜着能否通过,对角线 AC 的长最大,因此需要求出 AC 的长,怎样求呢?ABC1 m2 m【例 1 】有一个边长为 50dm 的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长?(结果保留整数)50dmABCD2222ACABBC5050500071(dm)【解析】 在 Rt△ ABC中,∠ B=90°, AB=BC=50dm,∴ 由勾股定理可知:【例题】 【跟踪训练】 如图,池塘边有两点 A,B ,点 C 是与 BA 方向成直角的 AC方向上的一点,测得 CB=60m , AC=20m ,你能求出 A,B 两点间的距离吗?(结果保留整数)【解析】在 Rt△ABC 中,AB= ,所以 A,B 两点间的距离是57m.22602057【例 2 】一个 2.5m 长的梯子 AB 斜靠在一竖直的墙 AC 上,这时 AC 的距离为 2.4m .如果梯子顶端 A 沿墙下滑 0.4m ,那么梯子底端 B 也外移 0.4m 吗? ABCDE【解析】在 Rt△ABC 中, ∠ ACB=90°, ∴ AC2+ BC2 = AB2 ,即 2.42+ BC2 = 2.52 , ∴BC = 0.7m.由题意得: DE = AB = 2.5m ,DC = AC - AD = 2.4 - 0.4 = 2(m).在 Rt△DCE 中, ∠ DCE=90°, ∴ DC2+ CE2 = DE2 ,即 22+ CE2 = 2.52,∴CE = 1.5m, ∴BE = 1.5 - 0.7 = 0.8m≠0.4m.答:梯子底端 B 不是外移 0.4m.【例题】 在我国古代数学著作《九章算术》中记载了一道有趣的问题 . 这个问题意思是:有一个水池,水面是一个边长为 10 尺的正方形 ,在水池的中央有一根新生的芦苇,它高出水面 1 尺,如果把这根芦苇拉向岸边,它的顶...