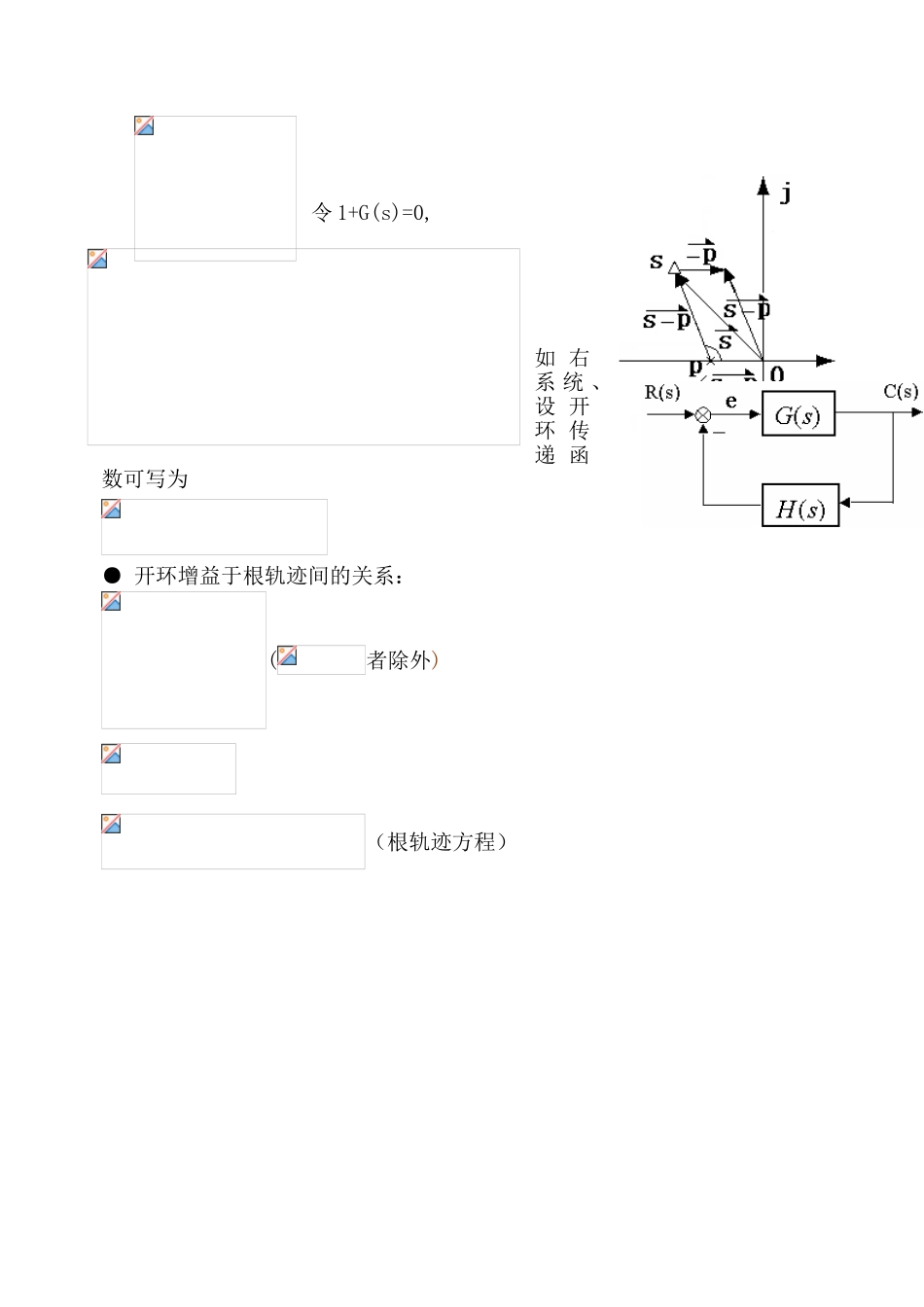
第四章 线性系统的根轨迹法闭环系统的性能由闭环零极点分布决定。当开环传递函数中某个参数变化时,闭环系统特征方程的系数也相应变化,闭环极点也要改变(解根难)。研究闭环极点随开环某参数变化而变化的规律,进而讨论闭环系统性能的变化趋势,是具有理论和实际工程意义的课题。(调参、设计等)。根轨迹的特点:●图解法,简单;●特别适用于研究当系统的开环参数变化时,系统性能的变化趋势问题;●近似方法,不十分精确。§4.1 根轨迹的基本概念1、根轨迹的概念:当开环系统某一参数从 0 到∞变化时,闭环极点在 S 平面上变化所描绘出的轨迹。例 1:系统如右: 根轨迹增益。闭环传递函数为: 闭环特征方程为:特征根为: , 当系统参数(或)从零变化到无穷时,闭环极点的变化情况如表4-1 所示。表 4-1 、=0~时系统的特征根000-20.50.25-0.3-1.710.5-1-121-1+j-1-j52.5-1+j2-1-j2∞∞-1+j∞-1-j∞ 3、闭环零极点与开环零极点之间的关系:例 2:系统如右:●闭环零点=前向通道的零点+反馈通道的极点(不随变化,易得 到,不必专门研究。)● 闭环极点与开环零点,开环极点和根轨迹增益都有关系(需专门研究)。4、根轨迹方程:例 3、如右系统令 1+G(s)=0,如 右系 统 、设 开环 传递 函数可写为 ● 开环增益于根轨迹间的关系:(者除外) (根轨迹方程)例 4、系统开环极点分布如右图所示,分别讨论是否在根轨迹上。● 任一点 S,总可以有一个与之对应,满足模值条件,但它不一定在根轨迹上(不一定满足相角条件)。● 满足相角条件的 S,也一定有对应的使之满足模值条件,所以相角条件是判定 S 在不在根轨迹上的充要条件。● 当 S 满足相角条件时,它一定在根轨迹上,所对应的值,由模值条件确定。§4.2 绘制根轨迹的基本法则1、 起点和终点:根轨迹起始于开环极点,终止于开环零点;如果开环零点个数少于开环极点个数 ,则有条根轨迹终止于无穷远处。起点:终点:2、根轨迹的分支数及对称性:3、实 轴上的根轨迹:从实轴最右端的开环零极点算起,奇数开环零极点到偶数开环零极点间一定是根轨迹,否则一定不是证明:见右图为例说明∴S是根轨迹上的点。● 定理:当开环极点有 2 个,开环零点有 1 个,并且在复平面上有根轨迹时,则复平面上的根轨迹一定是以零点为圆心的圆弧。证明:(见下面两页)要求:对于二阶系统的根轨迹,一定要能画的熟练准确。例:例 :单 位反 馈系 统其 开环 传递...