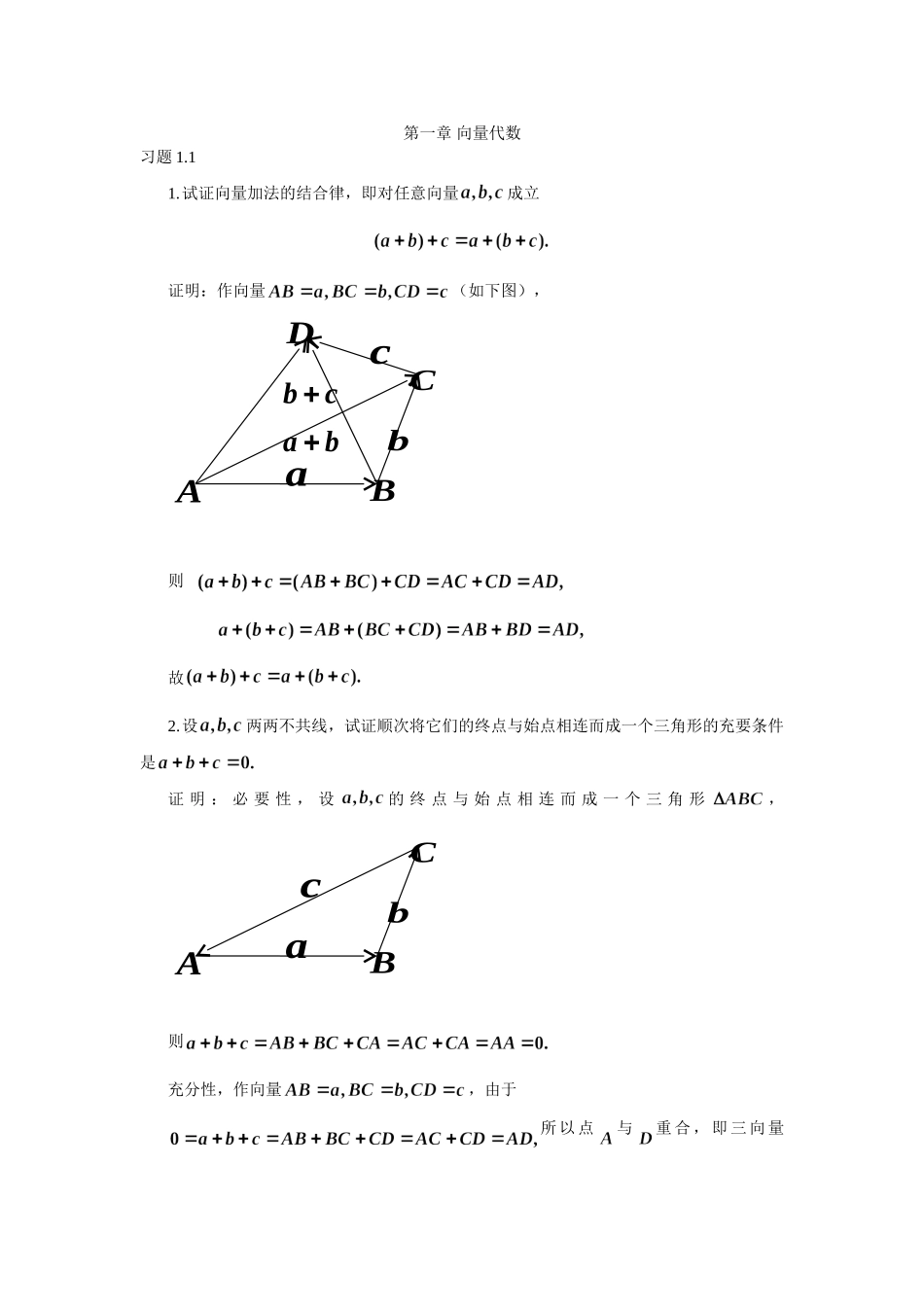
第一章 向量代数习题 1.11.试证向量加法的结合律,即对任意向量成立证明:作向量(如下图),则 故2.设两两不共线,试证顺次将它们的终点与始点相连而成一个三角形的充要条件是证 明 : 必 要 性 , 设的 终 点 与 始 点 相 连 而 成 一 个 三 角 形, 则充分性,作向量,由于所以点与重合,即三向量ABCDabcabbcABCabc的终点与始点相连构成一个三角形。3.试证三角形的三中线可以构成一个三角形。证明:设三角形三边的中点分别是(如下图),并且记, 则 根 据 书 中 例 1.1.1 , 三 条 中 线 表 示 的 向 量 分 别 是所以,故由上题结论得三角形的三中线可以构成一个三角形。4.用向量法证明梯形两腰中点连线平行于上、下底且等于它们长度和的一半。证明:如下图,梯形两腰中点分别为,记向量,则而向量与共线且同向,所以存在实数使得现在由于是的中点,所以且ABabc EFDABabEF故梯形两腰中点连线平行于上、下底且等于它们长度和的一半。5.试证命题 1.1.2。证明:必要性,设共面,如果其中有两个是共线的,比如是,则线性相关,从而线性相关。现在设两两不共线,则向量可以在两个向量上的进行分解,即作以为对角线,邻边平行于的平行四边形,则存在实数使得,因而线性相关。充分性,设线性相关,则存在不全为零的数,使得。不妨设,则向量可以表示为向量的线性组合,因此由向量加法的平行四边形法则知道向量平行于由向量决定的平面,故共面。6.设是不共线的三点,它们决定一平面,则点在上的充要条件是存在唯一的数组使得其中,是任意一点。在内的充要条件是(*)与同时成立。证明:必要性,作如下示意图,连接并延长交直线于。则 由 三 点共 线 , 存 在 唯 一 的 数 组使 得, 并 且。由三点共线,存在唯一的数组使得,并且。于是,设由,的 唯 一 性 知 道的 唯 一 性 , 则且。BCORP充分性,由已知条件有,得到,因而向量共面,即在决定的平面上。如果在内,则在线段内,在线段内,于是,则。如果(*)成立且,则有,这说明点在角内。同样可得到,这说明点在角内。故在内。7.在中,点分别在边与上,且与交于,试证证明:作如下示意图,由三点共线,存在使得,由三点共线,存在使得,由于有因而。由于向量不共线,所以,解此方程组得。由此得,BCR DE。同理得到。故得8.用向量法证明的三条中线交于一点,并且对任意一点有证明:设分别是边的中点,则交于一点,连接。...