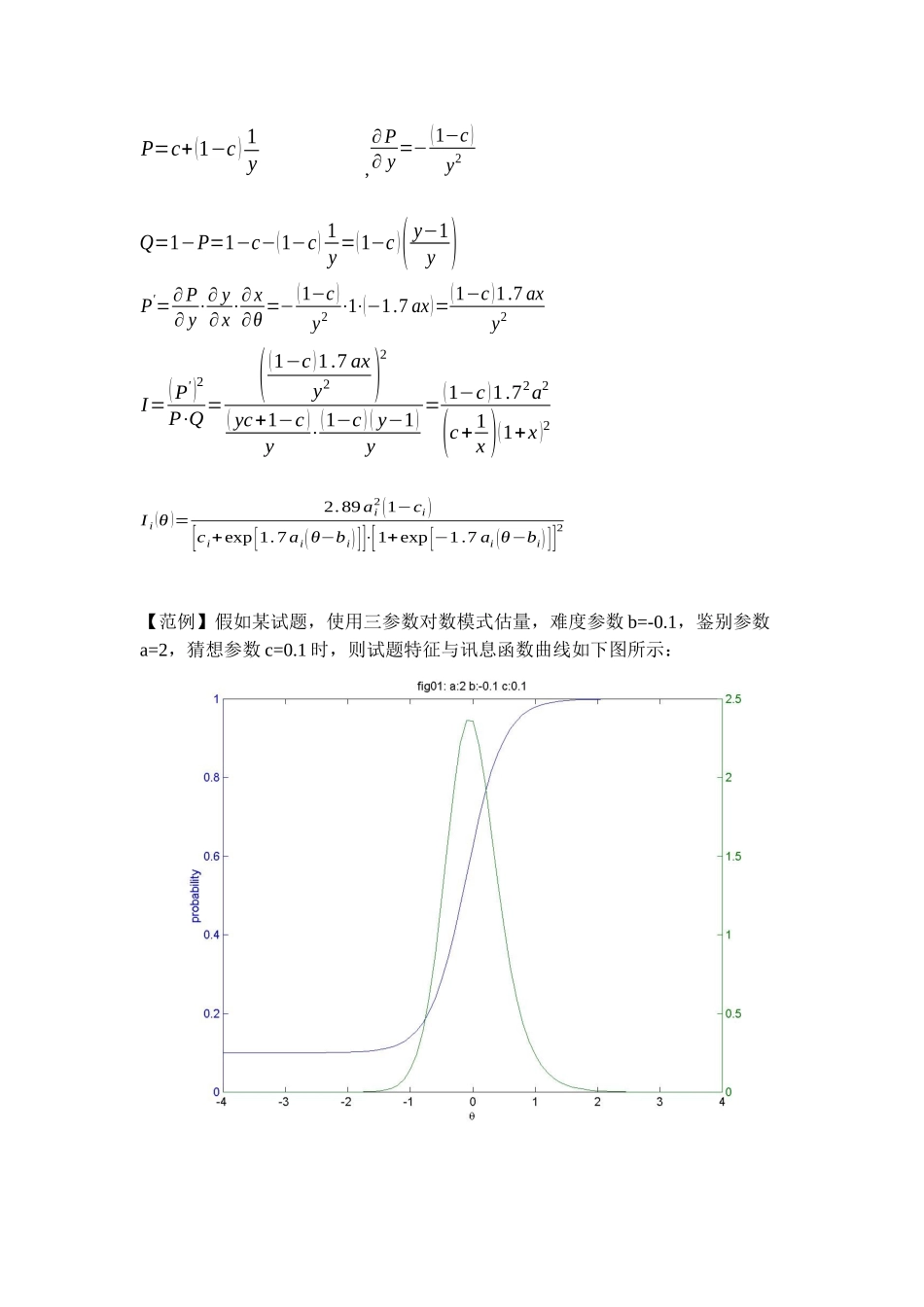
讯息函数试题反应理论有二个重要的曲线,一是试题特征曲线,二是试题讯息曲线,藉由试题的特征、讯息的二个曲线,来描述试题的潜在特性,经由选题而汇合成为试题数据库,经由计算机适性施测,可以达到个别化施测,由于施测试题的不同与方式的不同,可求得受测者的潜在能力。 试题讯息函数在实施计算机适性测验的进展过程中,无论在题库建立时,试题的筛选,或是在计算机施测的过程中,试题的选择,都占有非常重的角色。一、试题讯息函数(Item Information Function) 讯息函数可作为描述、选择测验试题、以及比对测验的相对效能的有用方法,且作为建立、分析与诊断测验的参考依据。试题讯息函数定义如下:I i (θ )=[Pi' (θ )]2Pi (θ) Qi (θ ) i=1,⋯,n <公式一>I i (θ ):能力θ 在试题 i 的试题讯息Pi (θ) :能力θ 在试题 i 的答对机率Qi (θ) :能力θ 在试题 i 的答错机率Pi' (θ) :能力θ 的反应函数导数假如试题估量使用三参数对数模式,其试题特征曲线的公式如下Pi (θ)=ci+1−ci1+exp(−1.7 ai (θ−bi)) <公式二>则试题讯函公式如下(Brinbaum, 1968; Lord, 1980)I i (θ )=2.89ai2(1−ci )[ci+exp[1.7ai(θ−bi)]]⋅[1+exp[−1.7 ai (θ−bi)]]2 <公式三>【证明】x=exp[−1.7a (θ−b )] ,∂x∂θ =−1.7axy=x+1 ,∂ y∂ x =1P=c+(1−c ) 1y ,∂ P∂ y =−(1−c )y2Q=1−P=1−c−(1−c) 1y =(1−c )(y−1y )P'=∂P∂ y⋅∂ y∂x⋅∂x∂θ =−(1−c )y2 ⋅1⋅(−1.7 ax)=(1−c )1.7 axy2I=(P')2P⋅Q =((1−c )1.7 axy2)2( yc+1−c )y⋅(1−c ) ( y−1)y=(1−c )1.72a2(c+ 1x )(1+x )2I i (θ )=2.89ai2(1−ci )[ci+exp[1.7ai(θ−bi)]]⋅[1+exp[−1.7 ai (θ−bi)]]2【范例】假如某试题,使用三参数对数模式估量,难度参数 b=-0.1,鉴别参数a=2,猜想参数 c=0.1 时,则试题特征与讯息函数曲线如下图所示:假如在能力参数为θmax的点上,θmax的值如下(Birnbaum, 1968)θmax=bi+11.7 ailn(1+√1+8ci2) <公式四>【证明】令z=c+ 1x ,∂ z∂ x =−1x2I=(1−c )1.72a2(c+ 1x)(1+x )2=1.72a2(1−c )zy 2=1.72a2 (1−c )y2 z∂ I∂θ=1.72a2(1−c )[−2y3⋅∂ y∂ x⋅∂ x∂θ⋅1z + 1y2⋅−1z2 ⋅∂ z∂ x⋅∂ x∂θ]令∂ I∂θ=0 ,θ 为θmax−2y ⋅1+−1z ⋅−1x2 =0y=2zx2x+1=2⋅(c+ 1x)⋅x2 ,1x...