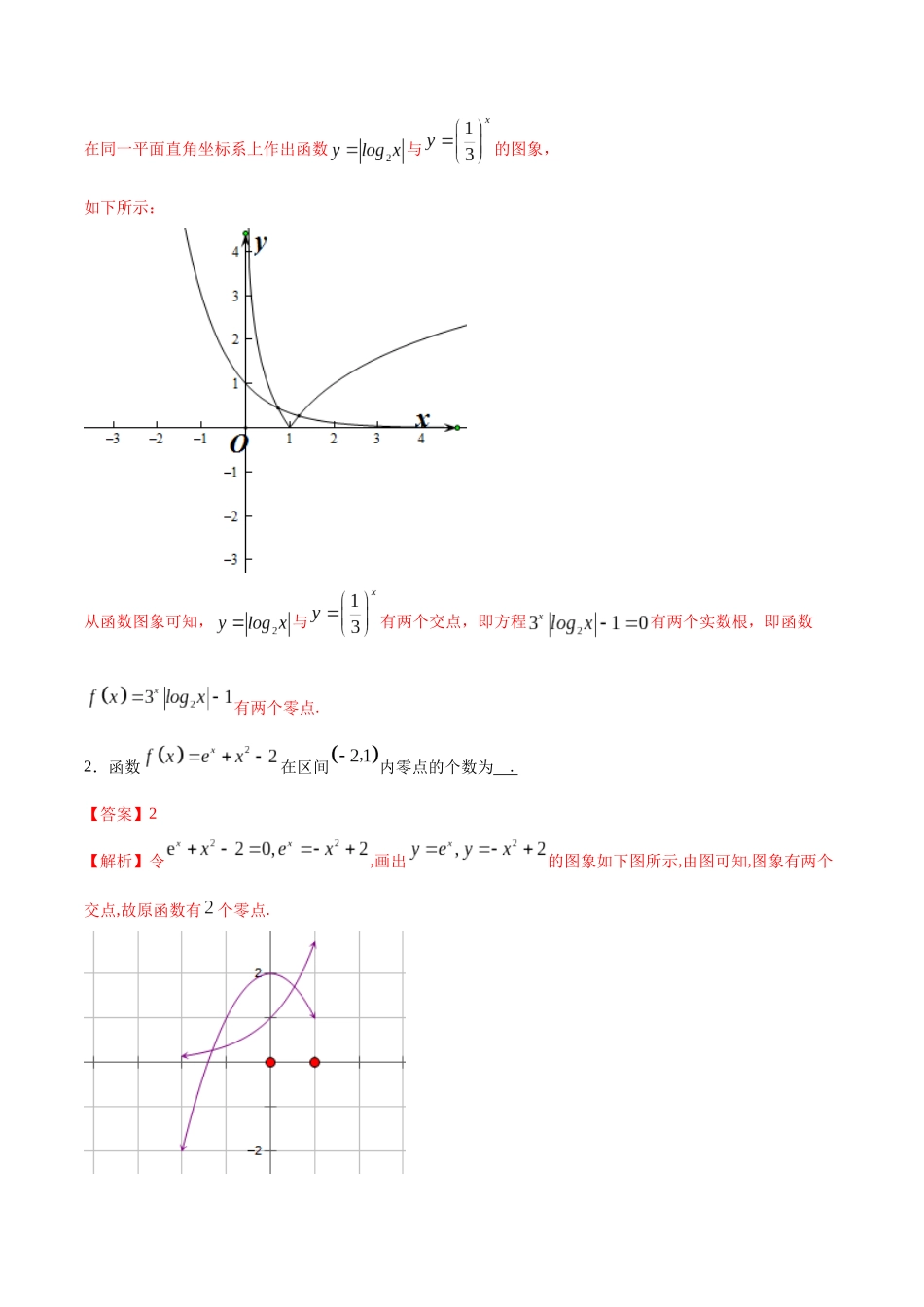
考点 12:零点定理【题组一 求零点】1.函数 f(x)的零点为_____.【答案】﹣3【解析】当时,;当时,,不满足,排除;故函数零点为 故答案为:2.若函数的零点为,则________.【答案】3【解析】根据题意,若函数 f(x)=log2(x+a)的零点为﹣2,则 f(﹣2)=log2(a2﹣ )=0,即 a2﹣ =1,解可得 a=3,故答案为 33.设函数,则函数的零点是________________.【答案】0 或 1【解析】等价于或,解得或,所以,函数的零点是 0 或 1.故答案为:0 或 1.【题组二 零点区间】1.函数的零点所在的一个区间是( )A.B.C.D.【答案】A【解析】,,所以,根据零点存在性定理,函数的零点所在的一个区间是,故选:A.2.已知函数.在下列区间中,包含零点的区间是( )A.B.C.D.【答案】D【解析】函数,在其定义域上连续,又,,故函数的零点在区间上.故选:D.3.函数在下列哪个区间必有零点( )A.B.C.D.【答案】B【解析】 ,,,∴,∴在区间内必有零点.故选:B.【题组三 零点个数】1.函数的零点个数为 . 【答案】2【解析】函数的零点,即方程的解,即,转化为函数与的交点,在同一平面直角坐标系上作出函数与的图象,如下所示:从函数图象可知,与有两个交点,即方程有两个实数根,即函数有两个零点.2.函数在区间内零点的个数为 . 【答案】2【解析】令,画出的图象如下图所示,由图可知,图象有两个交点,故原函数有个零点.3.函数 f(x)=cosπx﹣()x+1 在区间[1﹣ ,2]上的零点个数为 . 【答案】3【解析】根据题意可知,函数在区间上的零点的个数,即为函数的图象与函数的图象在区间上的交点的个数,在同一坐标系中画出两个函数图象如图所示:可以发现有三个公共点,所以函数在区间上有三个零点,4.函数的零点个数是 . 【解析】因为与均在上为增函数,所以函数至多一个零点又,,,即函数在上有一个零点.5.函数,则的零点个数为________.【答案】1【解析】函数定义域为令,则的零点的个数就是函数,的交点个数如上图所示,则的零点个数为 .故答案为:6.定义在 R 上的偶函数满足,且当时,,则的零点个数为____________.【答案】10【解析】由于定义在 R 上的偶函数满足,所以的图象关于直线对称,画出时,部分的图象如图,在同一坐标系中画出的图象,由图可知:当时,有 5 个交点,又和都是偶函数,所以在上也是有 5 个交点,所以的零点个数是 10,故答案为:10.7.函数的零点个数为_______________.【...