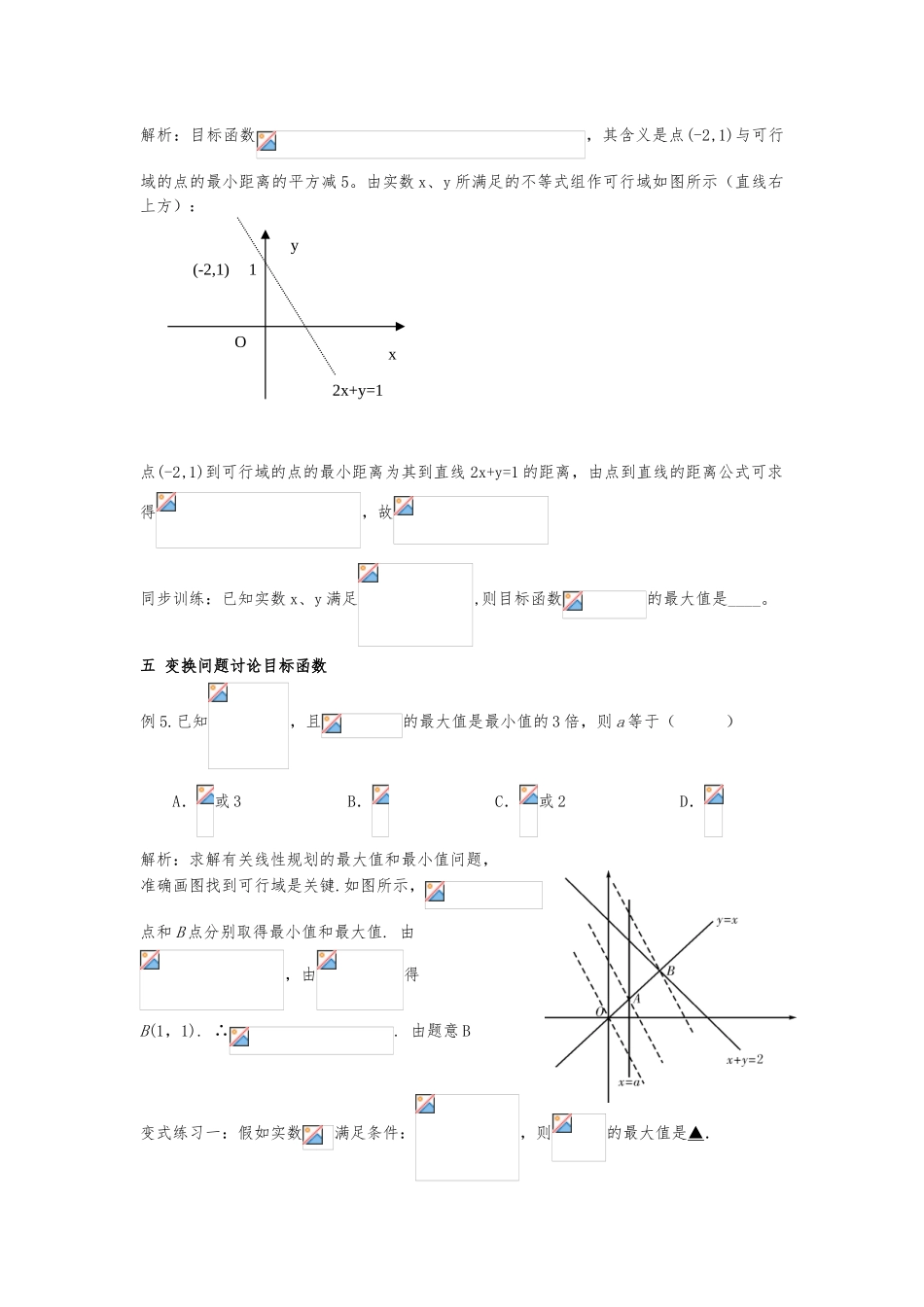
授课提纲一、线性规划问题中目标函数常见类型梳理1、基本类型——直线的截距型(或截距的相反数)2、直线的斜率型3、平面两点间的距离型(或距离的平方型)4、点到直线的距离型5、变换问题讨论目标函数二、基本不等式1、(1)基本不等式若,则 (2)若,则(当且仅当时取“=”) (2)若,则 (2)若,则(当且仅当时取“=”)(3)若,则 (当且仅当时取“=”)2、利用基本不等式求值技巧授课主要容:一 基本类型——直线的截距型(或截距的相反数)例 1.已知实数 x、y 满足约束条件,则的最小值为( )A.5 B.-6 C.10 D.-10 变式练习一:若 x,y 满足约束条件 ,则 z=3x+y 的最大值为.变式练习二:设 x,y 满足约束条件则 z=2x-y 的最大值为______.二 直线的斜率型例 2.已知实数 x、y 满足不等式组,求函数的值域.变式练习一:若 x,y 满足约束条件,则的最大值为.变式练习二:11.若实数满足,则的取值围为( )三 平面两点间的距离型(或距离的平方型)例 3. 已知实数 x、y 满足,则的最值为___________.解析:目标函数,点(2,2)到点 B 的距离为其到可行域点的最大值,;点(2,2)到直线 x+y-1=0 的距离为其到可行域点的最小值,。变式练习一:设实数,满足约束条件 则的取值围是(A)(B)(C)(D)变式练习二:四 点到直线的距离型例 4.已知实数 x、y 满足的最小值。解析:目标函数,其含义是点(-2,1)与可行域的点的最小距离的平方减 5。由实数 x、y 所满足的不等式组作可行域如图所示(直线右上方):点(-2,1)到可行域的点的最小距离为其到直线 2x+y=1 的距离,由点到直线的距离公式可求得,故同步训练:已知实数 x、y 满足,则目标函数的最大值是____。五 变换问题讨论目标函数例 5.已知,且的最大值是最小值的 3 倍,则 a 等于( )A.或 3 B. C.或 2 D.解析:求解有关线性规划的最大值和最小值问题,准确画图找到可行域是关键.如图所示,点和 B 点分别取得最小值和最大值. 由,由得B(1,1). ∴. 由题意 B变式练习一:假如实数满足条件:,则的最大值是▲.(-2,1)1Oxy2x+y=1基本不等式考点一:求最值例 1:求下列函数的值域(1)y=3x2+ (2)y=x+技巧一:凑项例 1:已知,求函数的最大值。技巧二:凑系数例 1. 当时,求的最大值。技巧三: 分离例 3. 求的值域。技巧四:换元解析二:本题看似无法运用基本不等式,可先换元,令 t=x+1,化简原式在分离求最值...