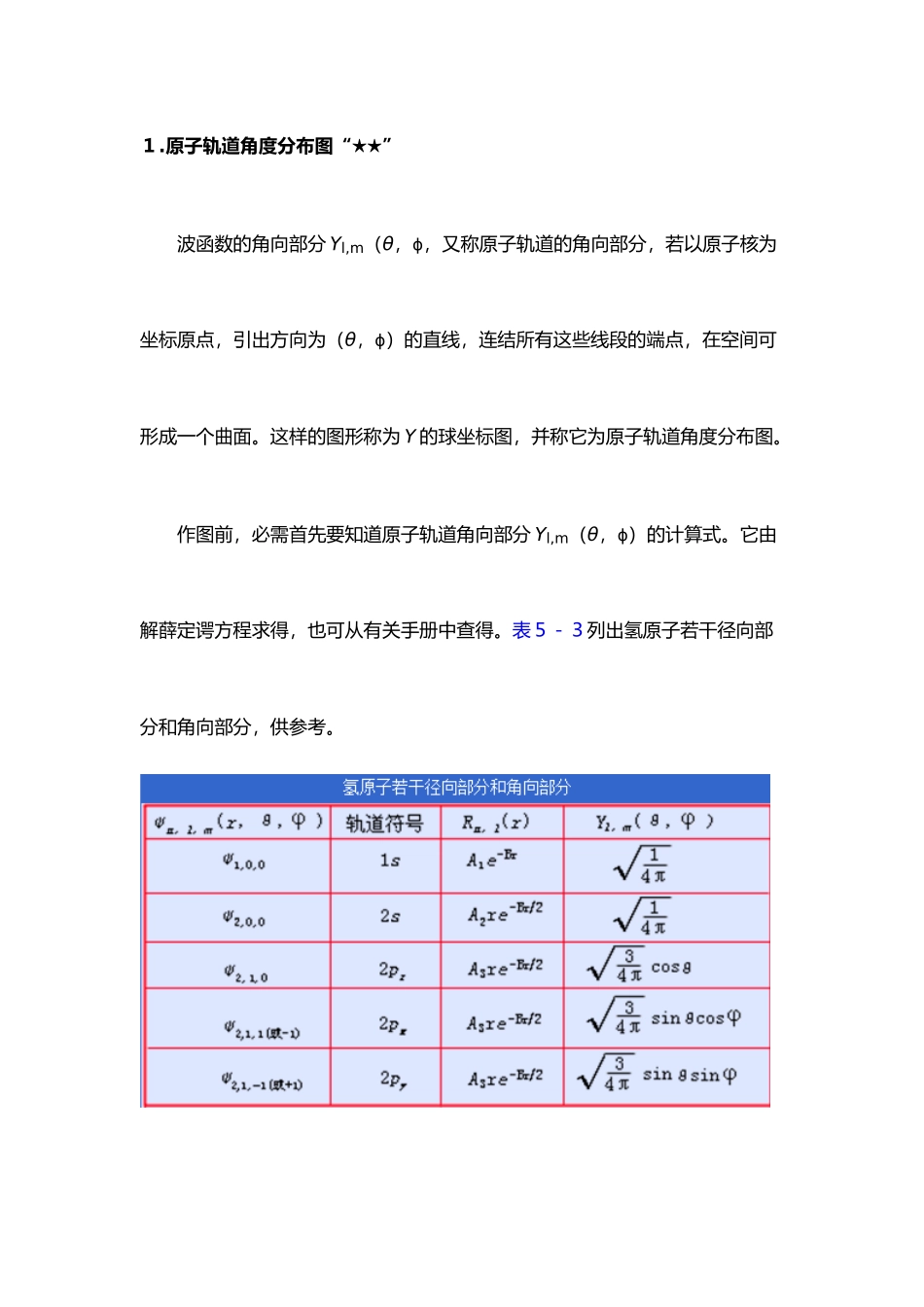
1.原子轨道角度分布图“★★” 波函数的角向部分 Yl,m(θ,ϕ,又称原子轨道的角向部分,若以原子核为坐标原点,引出方向为(θ,ϕ)的直线,连结所有这些线段的端点,在空间可形成一个曲面。这样的图形称为 Y 的球坐标图,并称它为原子轨道角度分布图。 作图前,必需首先要知道原子轨道角向部分 Yl,m(θ,ϕ)的计算式。它由解薛定谔方程求得,也可从有关手册中查得。表5-3列出氢原子若干径向部分和角向部分,供参考。例如 氢原子 [例 5-1] 画出氢原子 1s 原子轨道角度分布图 Y。 解:由解薛定谔方程可知从上式可知,Y1s 只是一个常数,与 θ, 角度无关。画出的氢原子 1s 原子轨道角度分布图是一个球曲面。半径为(1/4π)1/2。 由于原子轨道的角向部分 Yl,m(θ,ϕ)只与量子数 l,m 有关,而与主量子数 n 无关。因此,1s,2s,3s 原子轨道的角度分布图都是一样的球曲面。p,d,f 系列原子轨道同样如此。故在原子轨道角度分布图中,常不标明轨道符号前的主量子数。 [例 5-2] 画出 2pz 原子轨道角度分布图。 解:由解薛定谔方程可知 Y2pz = (3/4π)1/2cosθ(与 无关) 或 Ypz = K·cosθ 式中 K 为常数,对于 Y2pz,K 值为(3/4π)1/2,对于其它 p 轨道 K 值可能不同,但它不会影响图形的形状。 一些随 θ 角度而变化的 Ypz 和 Y2pz 值见表5-4。 利用表中列出的数据,可以在 xz 平面画出如图5-11所示的曲线。将曲线绕 Z 轴旋转一周(360°),可以得到“哑铃型”的立体曲面。由于Yp 值在 Z 轴方向(θ=0°)出现了极大值,所以该曲面图我们称为 p 原子轨道角度分布图,记为 Ypz,通常以其剖面图表示。 用以上类似的方法,我们可以画出 s,p,d 各种轨道的角度分布剖面图,如图5-12所示。 2.电子云角度分布图“★★” 假如我们将简化的薛定谔方程两边平方,则得到 ψ2n,l,m(r,θ,ϕ)= R2n,l(r)·Y2l,m(θ,ϕ) 电子云径向部分角向部分 上式中,ψ2n,l,m(r,θ,ϕ)的图像即为电子云的图象,它由二部分组成。一是电子云的径向部分 R2n,l(r),即几率密度随离核半径的变化,它与 θ,ϕ 角度无关;二是电子云的角向部分 Y2l,m(θ,ϕ),即几率密度只随角度 θ,ϕ 变化,它与主量子数 n,离核半径 r 无关。 电子云角度分布图的画法过程与原子轨道角度分布图一样,只需先将该原子轨道的角向分布·Yl,m(θ,ϕ)的计...