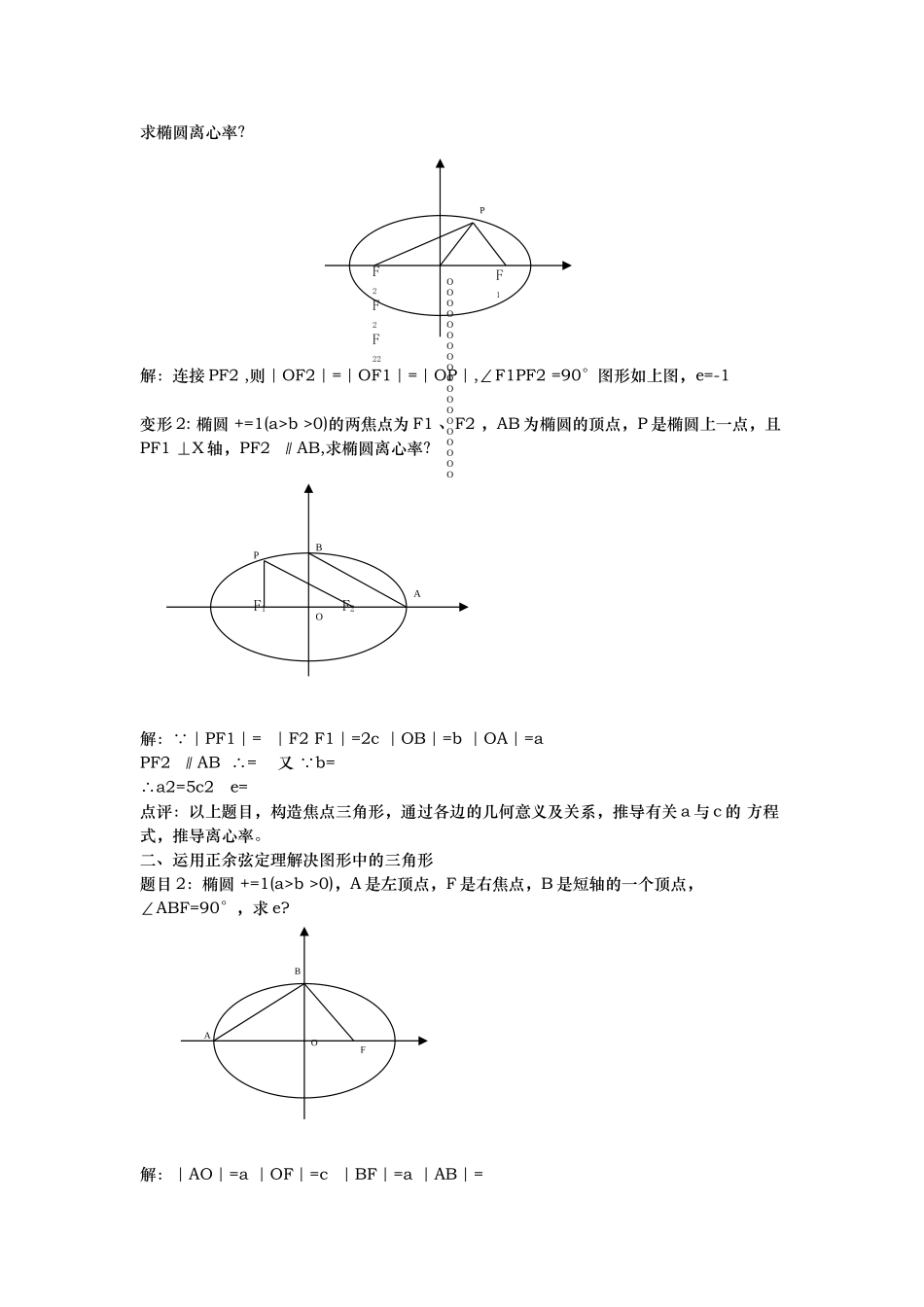
椭圆离心率的解法一、运用几何图形中线段的几何意义。基础题目:如图,O 为椭圆的中心,F 为焦点,A 为顶点,准线 L 交 OA 于 B,P、Q 在椭圆上,PD⊥L 于 D,QF⊥AD 于 F,设椭圆的离心率为 e,则① e=②e=③e=④e=⑤e=评:AQP 为椭圆上的点,根据椭圆的第二定义得,①②④。 |AO|=a,|OF|=c,∴有⑤; |AO|=a,|BO|= ∴有③。题目 1:椭圆 +=1(a>b >0)的两焦点为 F1 、F2 ,以 F1F2 为边作正三角形,若椭圆恰好平分正三角形的两边,则椭圆的离心率 e?思路:A 点在椭圆外,找 a、b、c 的关系应借助椭圆,所以取 AF2 的中点 B,连接 BF1 ,把已知条件放在椭圆内,构造△F1BF2 分析三角形的各边长及关系。解: |F1F2|=2c |BF1|=c |BF2|=cc+c=2a ∴e= = -1 变形 1:椭圆 +=1(a>b >0)的两焦点为 F1 、F2 ,点 P 在椭圆上,使△OPF1 为正三角形,DBFOBBBAPQBAF2F1求椭圆离心率? 解:连接 PF2 ,则|OF2|=|OF1|=|OP|,∠F1PF2 =90°图形如上图,e=-1 变形 2: 椭圆 +=1(a>b >0)的两焦点为 F1 、F2 ,AB 为椭圆的顶点,P 是椭圆上一点,且PF1 ⊥X 轴,PF2 ∥AB,求椭圆离心率? 解: |PF1|= |F2 F1|=2c |OB|=b |OA|=aPF2 ∥AB ∴= 又 b= ∴a2=5c2 e=点评:以上题目,构造焦点三角形,通过各边的几何意义及关系,推导有关 a 与 c 的 方程式,推导离心率。二、运用正余弦定理解决图形中的三角形题目 2:椭圆 +=1(a>b >0),A 是左顶点,F 是右焦点,B 是短轴的一个顶点,∠ABF=90°,求 e? 解:|AO|=a |OF|=c |BF|=a |AB|=OOOOOOOOOOOOOOOOOOOPF1F2 F2F22BAF2F1POFBAOa2+b2+a2 =(a+c)2 =a2+2ac+c2 a2-c2-ac=0 两边同除以 a2 e2+e-1=0 e= e=(舍去)变形:椭圆 +=1(a>b >0),e=, A 是左顶点,F 是右焦点,B 是短轴的一个顶点,求∠ABF?点评:此题是上一题的条件与结论的互换,解题中分析各边,由余弦定理解决角的问题。答案:90°引申:此类 e=的椭圆为优美椭圆。性质:1、∠ABF=90°2、假设下端点为 B1 ,则 ABFB1 四点共圆。3、焦点与相应准线之间的距离等于长半轴长。总结:焦点三角形以外的三角形的处理方法根据几何意义,找各边的表示,结合解斜三角形公式,列出有关 e 的方程式。题目 3:椭圆 +=1(a>b >0),过左焦点 F1 且倾斜角为 60°的直线交椭圆与 AB 两点,若|F1A|=2|BF1|,求...