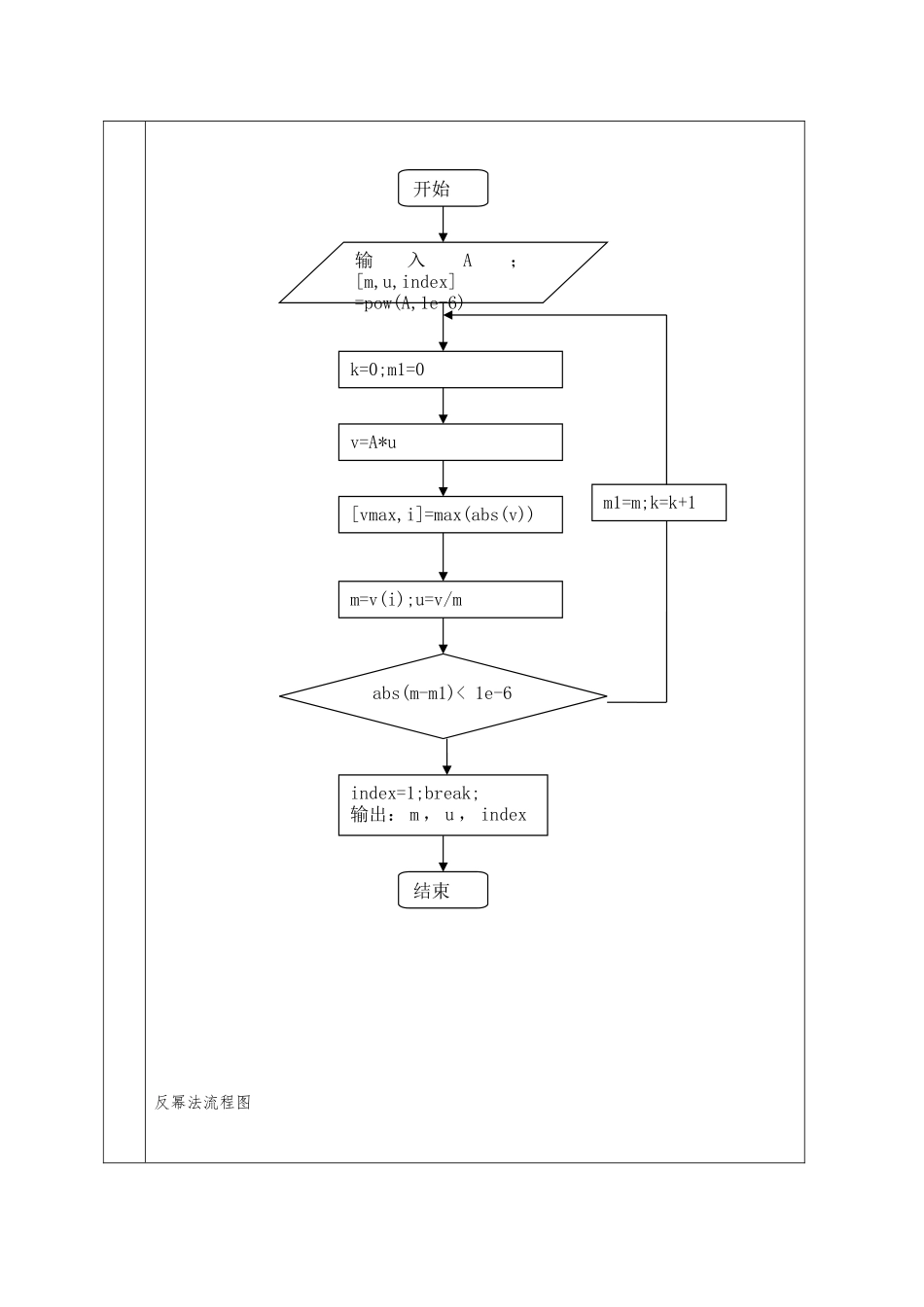
题目幂法和反幂法求矩阵特征值 课程设计具体容随机产生一对称矩阵,对不同的原点位移和初值(至少取 3 个)分别使用幂法求计算矩阵的主特征值与主特征向量,用反幂法求计算矩阵的按模最小特征值与特征向量,并比较不同的原点位移和初值说明收敛。要求1.仔细读题,了解问题的数学原形;2.选择合适问题求解的数值计算方法;3.设计程序并进行计算;4.对结果进行解释说明;采纳方法与结果说明对于幂法和反幂法求解矩阵特征值和特征向量的问题将从问题分析,算法设计和流程图,理论依据,程序与结果进行阐述该问题。一.问题的分析:求 n 阶方阵 A 的特征值和特征向量,是实际计算中常常碰到的问题,如:机械、结构或电磁振动中的固有值问题等。对于 n 阶矩阵 A,若存在数和 n 维向量 x 满足 Ax=x (1)则称为矩阵 A 的特征值,x 为相应的特征向量。由高等代数知识可知,特征值是代数方程|I-A|=+a+…+a+a =0 (2)的根。从表面上看,矩阵特征值与特征向量的求解问题似乎很简单,只需求解方程(2)的根,就能得到特征值,再解齐次方程组 (I-A)x=0 (3)的解,就可得到相应的特征向量。上述方法对于 n 很小时是可以的。但当 n 稍大时,计算工作量将以惊人的速度增大,并且由于计算带有误差,方程(2)未必是精确的特征方程,自然就不必说求解方程(2)与(3)的困难了。幂法是一种计算矩阵主特征值(矩阵按模最大的特征值)与对应特征向量的迭代方法,特别是用于大型稀疏矩阵。反幂法是计算海森伯格阵或三角阵的对应一个给定近似特征值的特征向量的有效方法之一。二.算法设计与流程图1、幂法算法(1)取初始向量 u(例如取 u=(1,1,…1) ),置精度要求,置 k=1. (2)计算v=Au,m =max(v), u= v/ m(3)若| m = m|<,则停止计算(m 作为绝对值最大特征值,u作为相应的特征向量)否则置 k=k+1,转(2)2、反幂法算法(1)取初始向量 u(例如取 u=(1,1,…1) ),置精度要求,置 k=1. (2)对 A 作 LU 分解,即 A=LU(3)解线性方程组 Ly=u,Uv=y(4)计算 m =max(v), u= v/ m(5)若|m =m|<,则停止计算(1/m 作为绝对值最小特征值,u作为相应的特征向量);否则置 k=k+1,转(3).幂法流程图:反幂法流程图开始输入A;[m,u,index]=pow(A,1e-6)k=0;m1=0v=A*u[vmax,i]=max(abs(v))m=v(i);u=v/mabs(m-m1)< 1e-6index=1;break;输出: m , u , index结束m1=m;k=k+1三、算法的理论依据与其推导...