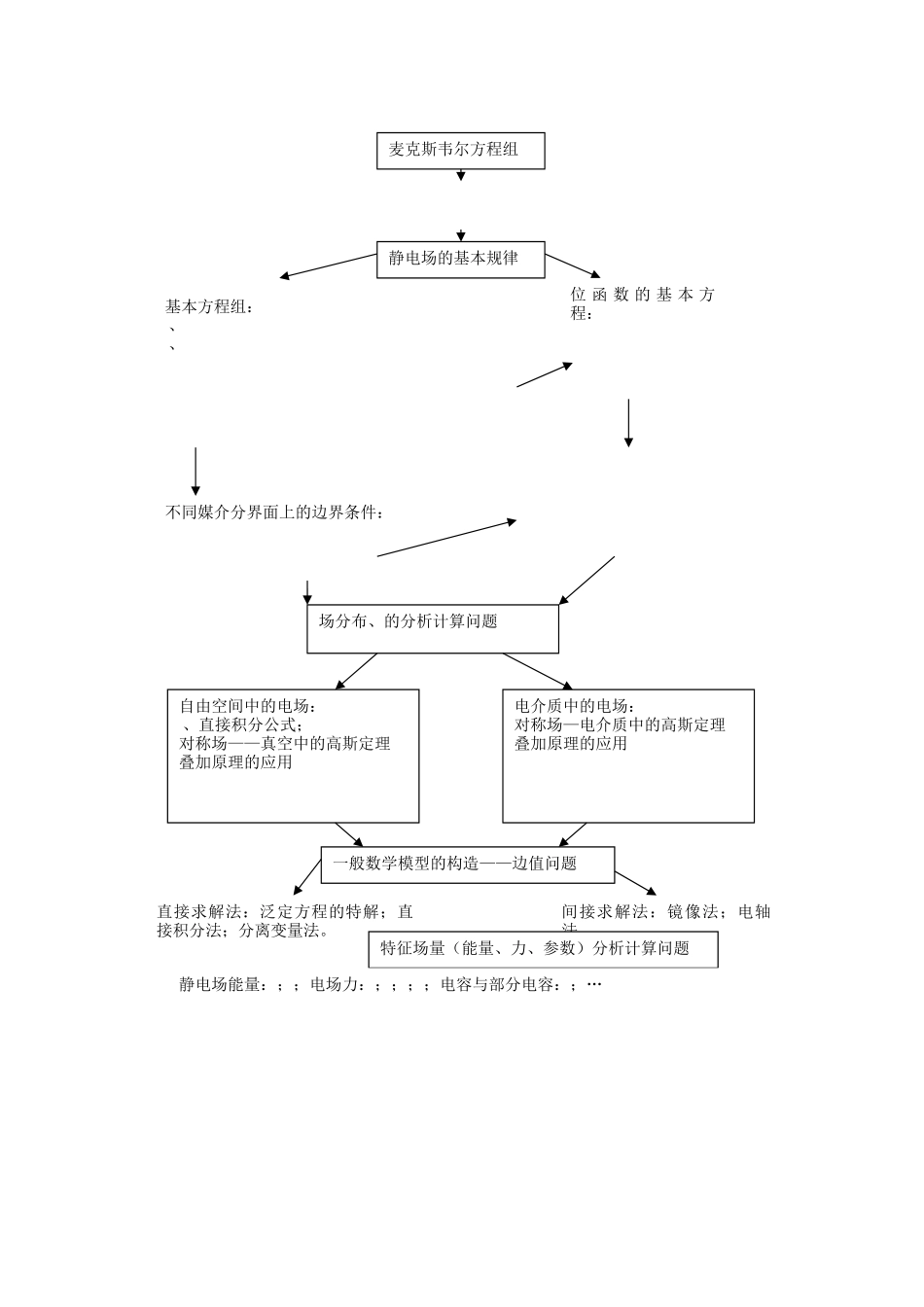
第一部分:电磁场的数学工具和物理模型 来源:工程电磁场原理老师手册场的概念;场的数学概念;矢量分析;数学工具:在不同坐标系下的数学描述方法;巩固标量场梯度的概念和数学描述方法;掌握散度在直角坐标系下的表达形式;掌握旋度在直角坐标系下的表达形式;强调几个矢量分析的恒等式:(任何标量函数梯度的旋度恒等于零);(任意 矢 量 函 数 旋 度 的 散 度 恒 等 于 零 ) ;;;。亥姆霍兹定理推导出:无旋场(场中旋度处处为零),但散度不为零;无散场(无源场)场中散度处处为零,但其旋度不为零;一般矢量场:场中散度和旋度均不为零。无限空间中的电磁场作为矢量场按定理所述,其特性取决于它的散度和旋度特性,而用公式可以表示为:,其中标量函数,矢量函数,由此可见,无限空间中的电磁场唯一地取决于其散度和旋度的分布。散度定理——高斯定理;旋度定理——stokes 定理第二部分:静态电磁场——静电场掌握电场基本方程,并理解其物理意义。电场强度与电位的定义以与物理含义;理解静电场的无旋性,与电场强度的线积分与路径无关的性质,以与电场强度与电位之间的联关系。掌握叠加原理,对自由空间中的静电场,会应用矢量分析公式计算简单电荷分布产生的电场强度与电位;对于呈对称性分布的特征的场,能熟练地运用高斯定理求解器电场强度与电位分布。了解媒介(电介质)的线性、均匀和各向同性的含义;了解电偶极子、电偶极矩的概念与其电场分布的特点。了解极化电荷、极化强度的定义与其物理意义。连接通过极化电荷求极化电场分布的积分形式。理解电位移矢量的定义,以与、和三者之间的关系。对电介质中的静电场,会求解其相应对称的场的分布。掌握电位所满足的偏微分方程(泊松方程和拉普拉斯方程),以与、和在不同媒介分界面上的衔接条件,能写出典型静电场问题所对应的数学模型——边值问题,并能求出一维边值问题的解,以与运用分离变量法求出在直接坐标系下二维边值问题的解。理解边值问题解的唯一性定理。掌握镜像法。能应用镜像法求解与圆柱、平板、球形导体相关,或以平面为界面的两种无限大的介质中的静电场问题。掌握电容参数计算的原则与方法。了解多导体系统的部分电容、工作电容的概念。理解静电屏蔽概念。理解电场能量与能量密度的概念,掌握具有对称性场分布的电场能量与其能量密度的计算方法。掌握基于电场强度定义公式的电场力的求取方法。理解广义力和广义坐标的概念、能量与力之间的功能...