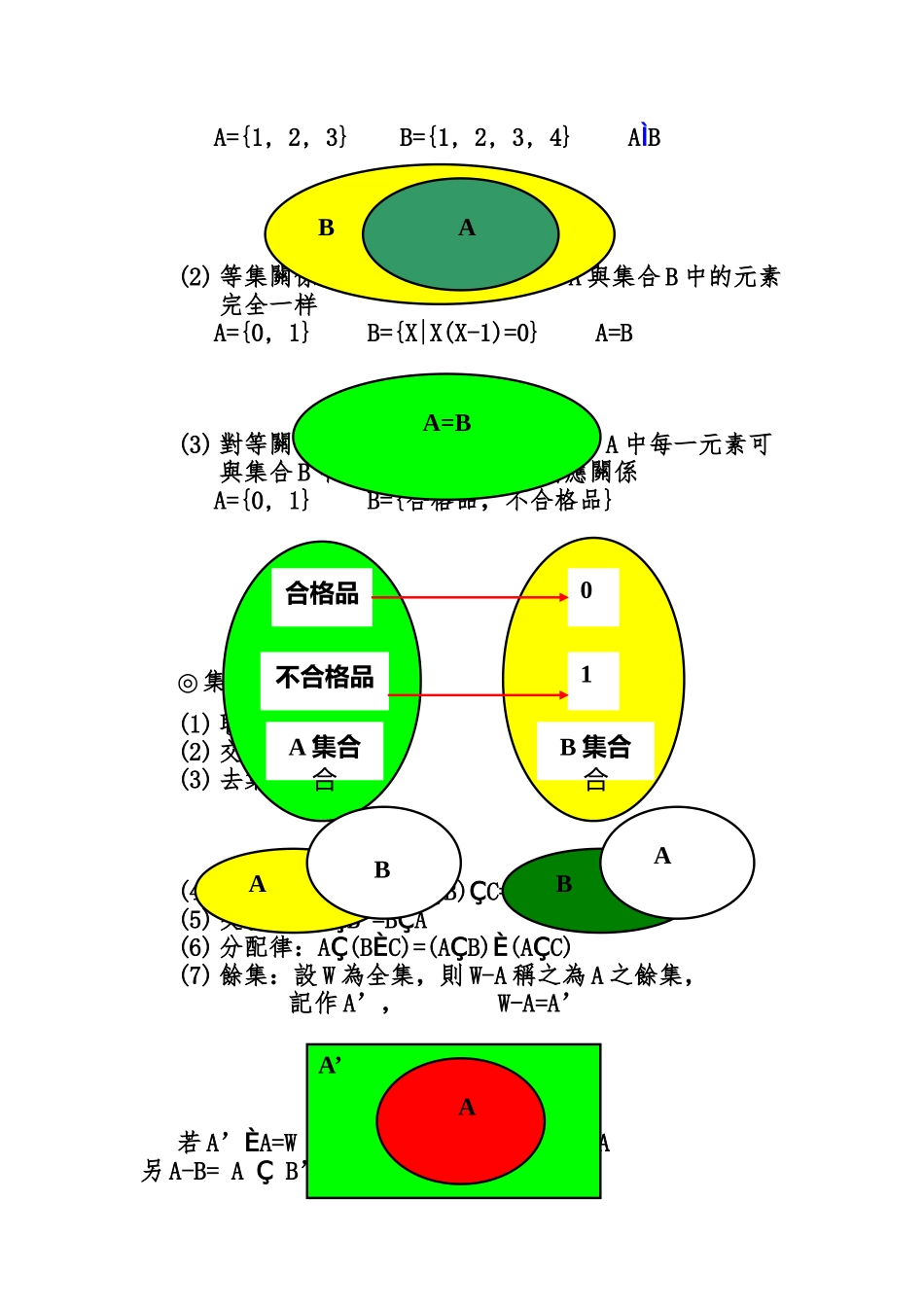
授課目錄第1章導論第2章統計資料的整理與描述第3章機率導論 第4章常用的機率分佈與統計分佈第5章描樣方法與描樣分佈第6章統計估計第7章統計檢定第8章變異數分析第9章相關分析與迴歸模式第10章 無母數統計檢定第11章 類別資料分析---列聯表與卡方檢定3.1 集合論◎ 集合論(Set Theory)à 機率論(Probability)à 群體分佈◎ 集合是元素的聚合,而元素是集合的單位。A={1, 2, 3}1, 2, 3 為 A 集合的單位 1ÎA無元素的集合存在,稱之為空集合,記做{ }或 Æ例集合 B={X|X2+6X+5=0}求 B={-1, -5}◎ 元素和集合的關係A={1, 2, 3} 1ÎA; 4ÏA◎ 集合和集合的關係(1) 子集關係:AÌB(A 含於 B 或 B 包含 A)即 A 中任一元素均在 B 集合中可找到第三章 機率論A={1, 2, 3}B={1, 2, 3, 4}AÌB(2) 等集關係:A=B(A 等於 B)即集合 A 與集合 B 中的元素完全一样A={0, 1}B={X|X(X-1)=0}A=B(3) 對等關係:A~B(A 對等於 B) 即集合 A 中每一元素可與集合 B 中的每一元素一對一對應關係A={0, 1}B={合格品,不合格品}◎ 集合之運算(1) 聯集運算:AÈB(2) 交集運算:AÇB(3) 去集運算:A-B(4) 結合律:A B C=(A B) C=A (B C)Ç ÇÇÇÇÇ(5) 交換律:A B =B AÇÇ(6) 分配律:A (B C)=(A B) (A C)ÇÈÇÈÇ(7) 餘集:設 W 為全集,則 W-A 稱之為 A 之餘集,記作 A’,W-A=A’若 A’ A=WÈA’ A=ÇÆ(A’)’=A另 A-B= A B’ÇBAA=B合格品不合格品A 集合合B 集合合10BAABA’A(8) 分割:設 W 為全集,集合 A、B 均含於 W,當滿足(a)A B=WÈ(b) A B=ÇÆ 時,則稱為 A、B 為 W 上的分割。(9) 餘集律:(A B)’=A’ B’ÈÇ(A B)’=A’ B’ÇÈ******************符號說明:X:隨機變數,P:機率,p:不合格率p(x):機率密度函數(離散型)f(x):機率密度函數(連續型)F(x):累積機率分配函數(連續型、離散型)E[X] = m (期望值),V[X] = s2 (變異數)m :母體平均值,s2:母體變異數:樣本平均值,S2:樣本變異數***********************3.2 機率的概念◎ 機率論是現代統計學的基礎。機率是為了衡量不確定結果,而建構出來的一種測度。其中基本的概念為:※機率空間(Probability Space):系統中,集合所有可能出現的事件而構成的一個抽象空間,通常以 W 表示。有時亦稱樣本空間(Sample Space)或結果空間(Outcome Space)。※事件(Events)...