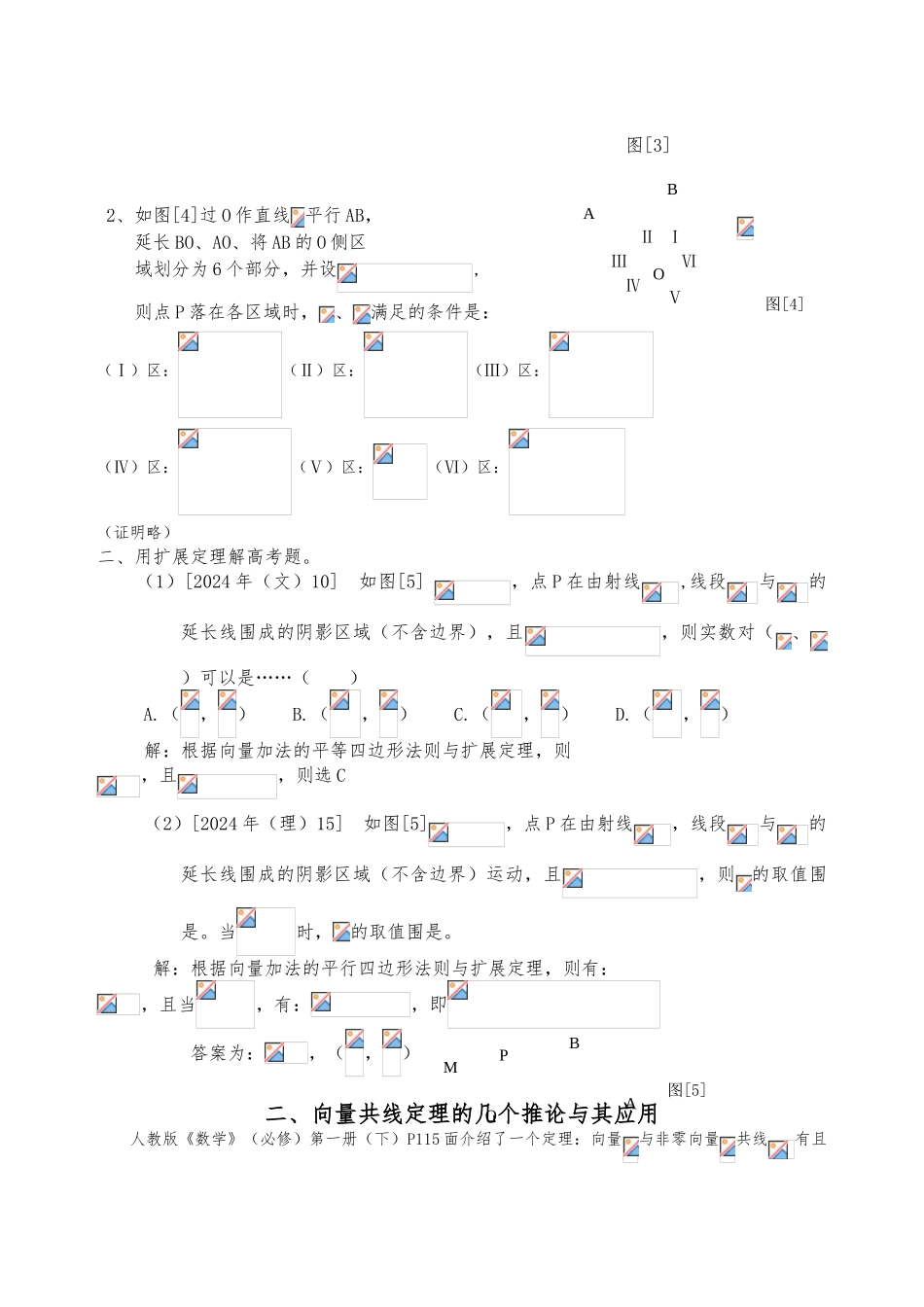
向量三点共线定理与其扩展应用详解一、平面对量中三点共线定理的扩展与其应用一、问题的提出与证明。1、向量三点共线定理:在平面中 A、B、C 三点共线的充要条件是:(O 为平面任意一点),其中。那么、时分别有什么结证?并给予证明。结论扩展如下:1、假如 O 为平面直线 BC 外任意一点,则 当时 A 与 O 点在直线 BC 同侧,时, A 与 O 点在直线 BC 的异侧,证明如下:设 且 A 与 B、C 不共线,延长 OA 与直线 BC 交于 A1点设 (≠0、≠1)A1与 B、C 共线则 存在两个不全为零的实数 m、n 且则 、(1) 则 则A 与 O 点在直线 BC 的同侧(如图[1])(2),则,此时与反向 A 与 O 在直线 BC 的同侧(如图[2])图[2](3),则 此时 A 与 O 在直线 BC 的异侧(如图[3])BCA11OAOA11BCAABCA11O图[1] 图[3]2、如图[4]过 O 作直线 平行 AB,延长 BO、AO、将 AB 的 O 侧区域划分为 6 个部分,并设,则点 P 落在各区域时,、满足的条件是:(Ⅰ)区:(Ⅱ)区:(Ⅲ)区:(Ⅳ)区:(Ⅴ)区:(Ⅵ)区:(证明略)二、用扩展定理解高考题。 (1)[2024 年(文)10] 如图[5] ,点 P 在由射线,线段与的延长线围成的阴影区域(不含边界),且,则实数对(、)可以是……( ) A.(,) B.(,) C.(,) D.(,) 解:根据向量加法的平等四边形法则与扩展定理,则,且,则选 C (2)[2024 年(理)15] 如图[5],点 P 在由射线,线段与的延长线围成的阴影区域(不含边界)运动,且,则的取值围是。当时,的取值围是。 解:根据向量加法的平行四边形法则与扩展定理,则有:,且当,有:,即 答案为:,(,)二、向量共线定理的几个推论与其应用人教版《数学》(必修)第一册(下)P115 面介绍了一个定理:向量与非零向量共线有且ABOⅢⅣⅤⅥⅠⅡMBAOP图[4]图[5]仅有一个实数,使=。谓之“向量共线定理”。以它为基础,可以衍生出一系列的推论,而这些推论在解决一些几何问题(诸如“三点共线”“三线共点”等)时有着广泛的应用。以下通过例题来加以说明。一、定理的推论推论一:向量与向量共线存在不全为 0 的实数,使,这实质是定理的另外一种表述形式。推论二:三个不同点 A、B、C 共线存在一组全不为 0 的实数,使。注意推论(二)与推论(一)的区别:推论(二)中均不为零向量,而推论(一)中,向量可能含。推论三: 设 O、A、B 三点不共线,且,...