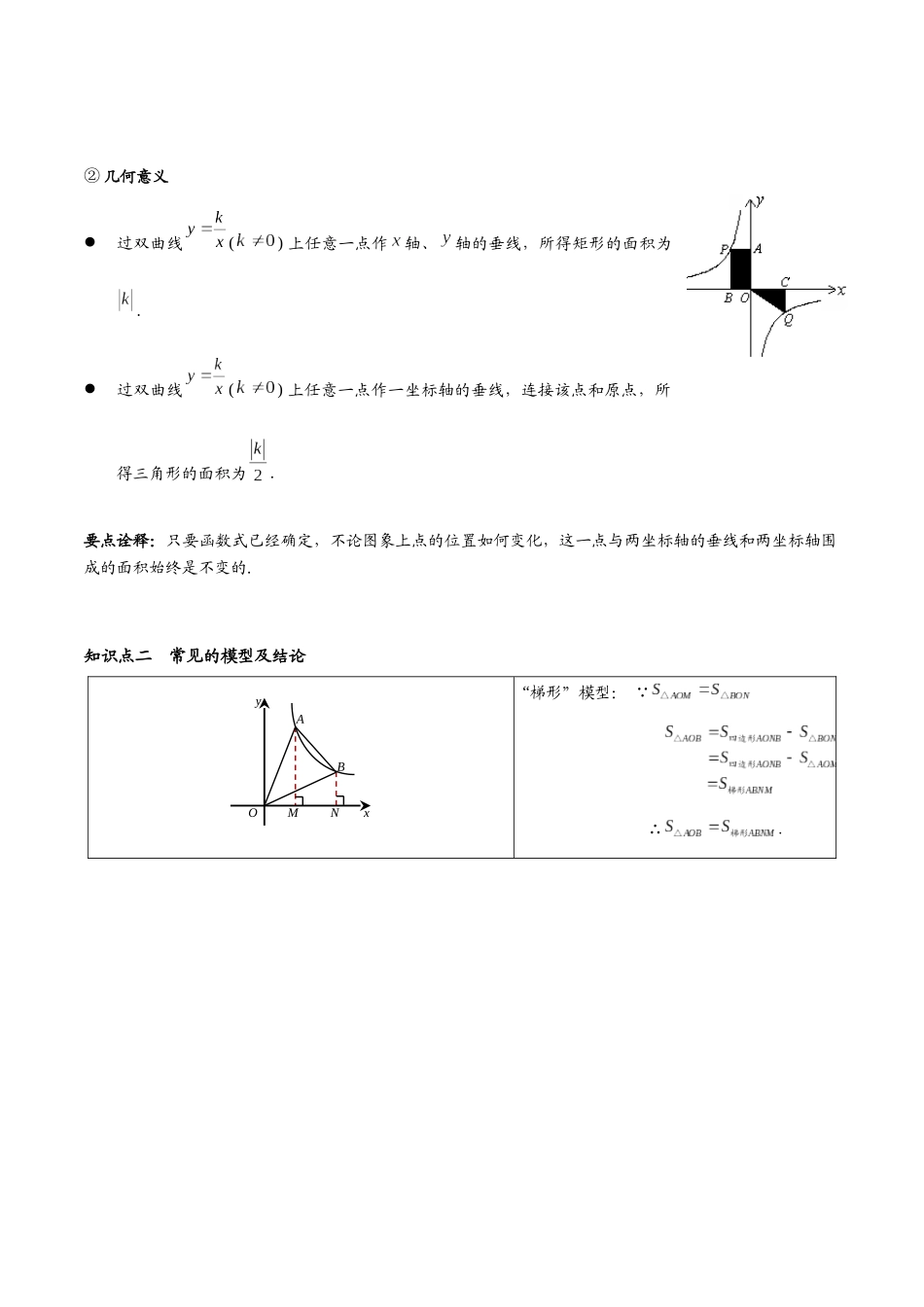
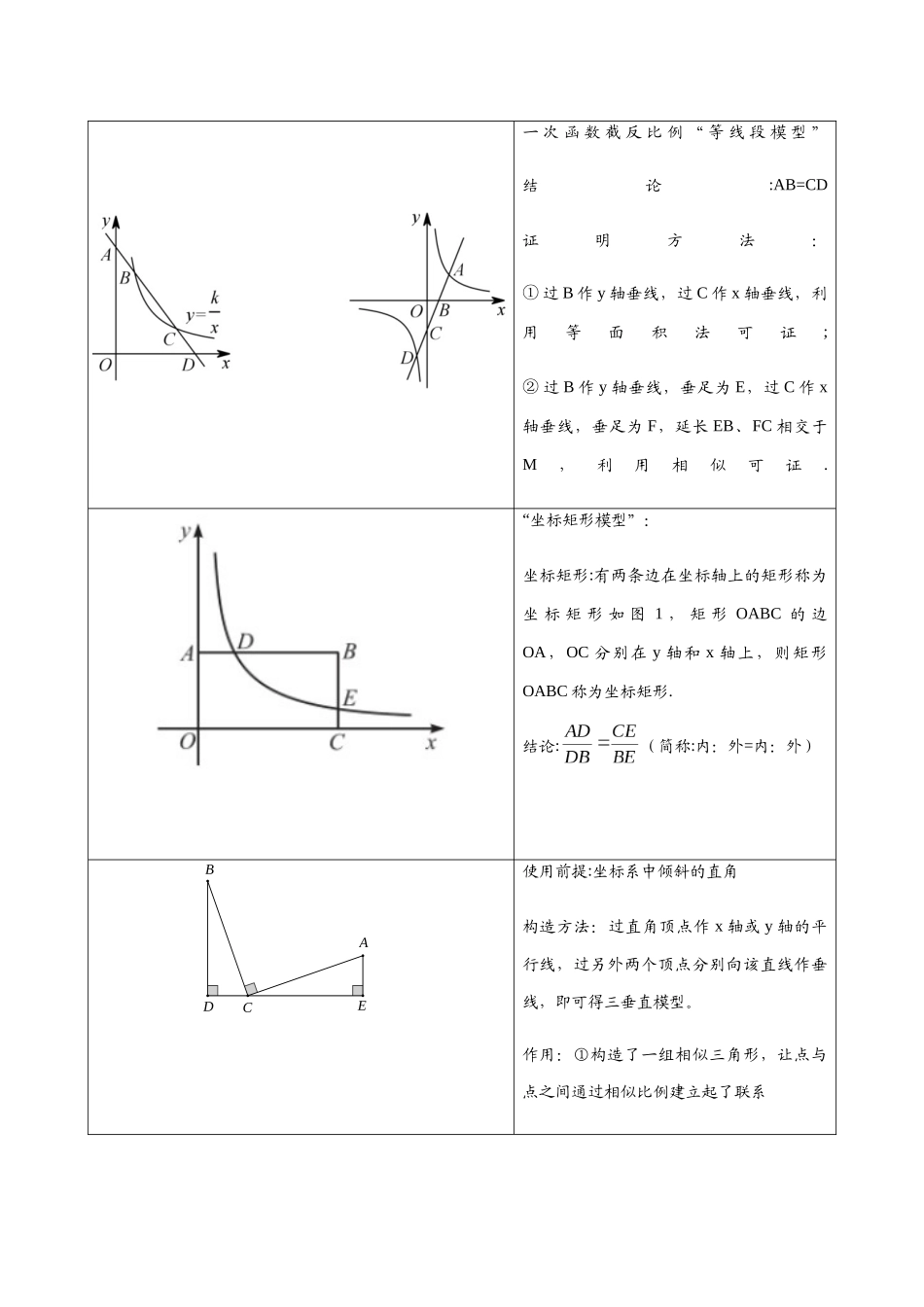
反比例函数与几何综合方法技巧呈现:考试中出现的反比例函数的综合计算题,不会单纯考查反比例函数的相关知识,一般都会和几何图形相结合.解决此类问题,既要掌握反比例函数的相关知识,又要能熟练应用坐标系中几何图形的相关知识.一:反比例函数与几何综合的处理思路:1.从关键点入手.“关键点”是信息汇聚点,通常是函数图像和几何图形的交点,通过关键点坐标和和横平竖直的线段长的互相转化可将函数特征与几何特征综合在一起进行讨论;2.梳理题干中的函数和几何信息,依次转化;3.借助函数特征或几何特征列方程求解.函数几何特征常见转化作法:1. 函数→坐标→几何 2. 几何→坐标函数① 借助表达式设出点坐标 ①讨论几何特征,考虑线段间关系:② 将点坐标转化为横平竖直线段长; ②通过设线段长进而表达点坐标③ 结合几何特征利用线段长列方程 ③将点坐标代入函数表达式列方程二:相关知识点知识点一 k 的代数意义和几何意义① 代数意义:反比例函数图象上的任意一点的横纵坐标之积等于比例系数 k.如图:若 A(m,n)和 B(s,t)为反比函数图像上两点;则有:mn=st.BAOxy② 几何意义过双曲线() 上任意一点作轴、轴的垂线,所得矩形的面积为.过双曲线() 上任意一点作一坐标轴的垂线,连接该点和原点,所得三角形的面积为.要点诠释:只要函数式已经确定,不论图象上点的位置如何变化,这一点与两坐标轴的垂线和两坐标轴围成的面积始终是不变的.知识点二 常见的模型及结论 yABOMNx“梯形”模型: ∴.一 次 函 数 截 反 比 例 “ 等 线 段 模 型 ”结论:AB=CD证明方法:① 过 B 作 y 轴垂线,过 C 作 x 轴垂线,利用等面积法可证;② 过 B 作 y 轴垂线,垂足为 E,过 C 作 x轴垂线,垂足为 F,延长 EB、FC 相交于M,利用相似可证.“坐标矩形模型”:坐标矩形:有两条边在坐标轴上的矩形称为坐 标 矩 形 如 图 1 , 矩 形 OABC 的 边OA,OC 分别在 y 轴和 x 轴上,则矩形OABC 称为坐标矩形.结论:(简称:内:外=内:外)使用前提:坐标系中倾斜的直角构造方法:过直角顶点作 x 轴或 y 轴的平行线,过另外两个顶点分别向该直线作垂线,即可得三垂直模型。作用:①构造了一组相似三角形,让点与点之间通过相似比例建立起了联系ABCDE(1)一中 2024 级周考)如图,正方形 ABCD 的边 BC 在 x轴的负半轴上,其中 E 是 CD 边的中点,函数的图像经过点 A...