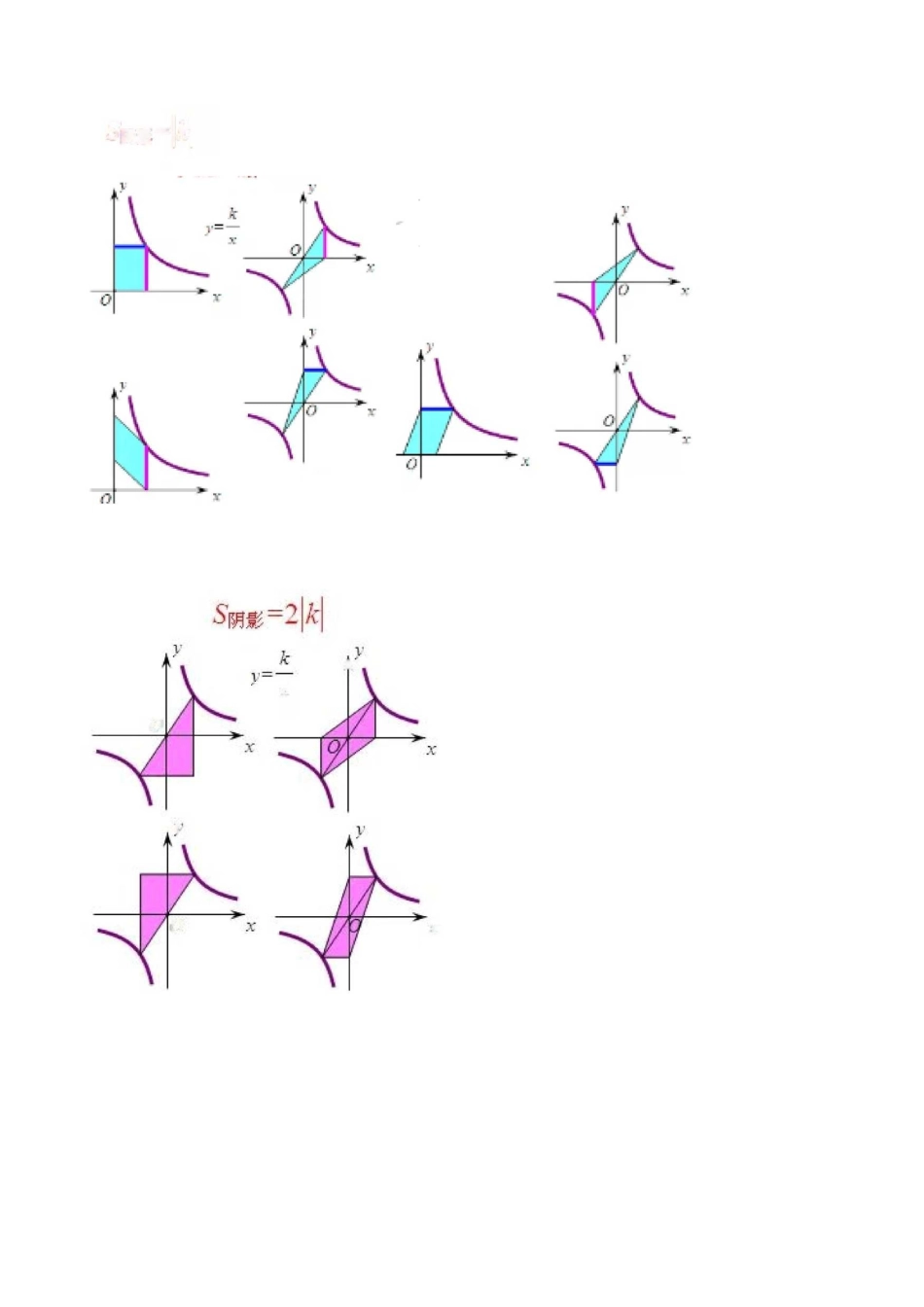
中考数学反比例函数中的考点大全、基本结论如圖过收曲线』=二上任一点也,V)A作 X 轴、丁轴的垂线班 PB,垂定温冬 B,则 s 导肚茄=x■丁=专卜■丁=?S^GB=^即过双曲线上任意一点;作坐标轴的垂践,2 坐标轴围戚的袒形面积杲定頑<.相应的,如果连接 P6 则■■-二、几种常见基本类型类型一:八XoIox三、实战分类型二:S 阴类型三:例:如團点)在双脱上,点在叹曲践A.〕=“上,且卫占冷工轴,GD 在 x 轴上,A若四辺形卫占①为袒形,求其面积.分析:由于点,点都在双曲线上,且都作了轴的垂线段,那么可以尝试向轴作垂线段,补成矩形,由于〃轴,则只需延长与轴相交即可,利用面积相减.解答:延长抽交丁轴于 E,易证四辺形 0C3E 为矩.形亠四辺形 OD.AE 为袒形■「则$兮 C-CEE=',5 公口血£=1.,5 自屈仞=1—1=】变式LBxxOBDOx如图,点卫在双曲线尸 Lt,点占在双曲缕尸二 t,点.C 在工轴上,卫月必轴,求 Zu 恥面积.分析:本题与例类似,由矩形换成了三角形,方法不变,因为〃轴,可考虑等积变形,将厶面积转化为△面积,然后继续延长,利用面积相减.解答:变连接月 Q30,易证 Sgc=SZED、延长加亵丁轴于 D■5-血尸斗'_1_31_„_耳疝门=:—〒=1,S^sc=1和XG5EFS如團点卫在双脱尸】上,点占在双UL 妙为辺作平行四^>ABCD,其中 GD 在 x 轴上,求 S^BCD-例分析:思路很简单,将平行四边形等积变形为矩形,而矩形面积又为两个小矩形面积之解答:过出作一匹丄工曲 E,过占作册丄卫 Wr 已易证子二曲尸-■'空手s3